Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Pressure in Liquids
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're going to explore the concept of pressure in liquids. Can anyone tell me what pressure is?
Isn't pressure the amount of force applied on a surface?
Exactly! Pressure is the force exerted by a liquid per unit area. Now, what factors do you think could affect the pressure at a given point in a liquid?
Maybe the depth of the liquid?
And the type of liquid, right? Like if it's denser or not?
Great points! Depth, liquid density, and gravitational acceleration are vital factors. Let's remember them using the acronym DDL - Depth, Density, and Lift (gravitational acceleration).
DDL sounds great! It helps remember what influences pressure.
Exactly! As we go deeper into the liquid, the pressure increases due to the weight of the liquid above. Can anyone share the formula for calculating pressure in a liquid?
It's P = Οgh, right?
Yes! A perfect recall! So remember, pressure at depth depends on the density of the liquid, the gravitational pull, and the depth itself.
Hydrostatic Pressure
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let's talk about hydrostatic pressure. Who can define what hydrostatic pressure is?
I think it's the pressure exerted by fluids at rest?
Right on target! Hydrostatic pressure comes from the weight of the liquid above. Can anyone tell me how this pressure acts?
I remember it acts in all directions.
Exactly! It acts in all directions and increases with depth. We can remember this using the phrase 'hydrostatic hights up' - height increases pressure! What factors affect hydrostatic pressure, class?
Density and depth!
Great! So we see density and depth again are crucial. What about the force experienced at different depths?
It increases!
Correct! The deeper you go, the higher the hydrostatic pressure due to more weight above. Remember this with DDL!
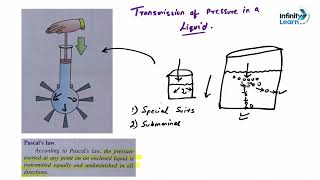
Pascalβs Law and Its Applications
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's shift gears and talk about Pascalβs Law. Who can explain it?
It says pressure applied to a fluid is transmitted equally throughout that fluid?
Spot on! This law is foundational for hydraulic systems. Can anyone give me examples of these systems?
Hydraulic lifts, like those at repair shops?
And car brakes use it too!
Fantastic examples! Remember the phrase 'Hydraulic Harmony' to describe how pressure is balanced in such systems. What do you understand by this transmission of pressure?
The pressure stays the same throughout and helps lift heavy objects easily.
Exactly! Thatβs the beauty of Pascalβs Law. Would you like to explore any specific applications further?
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section discusses the nature of pressure in liquids, its dependence on factors such as depth and density, and introduces Pascal's Law which states that pressure applied to a confined fluid is transmitted undiminished in all directions. The importance of hydrostatic pressure and buoyant force is also presented.
Detailed
Pressure in Liquids and Its Transmission
In this section, we delve into pressure in liquids, focusing on its definition, characteristics, and significance. Pressure in liquids is defined as the force exerted by the liquid per unit area, influenced by depth, density, and gravitational acceleration. The formula to calculate pressure at a specific depth is given by:
P = Οgh
Where:
- P = Pressure at a point in the liquid (in Pascals, Pa)
- Ο = Density of the liquid (in kg/mΒ³)
- g = Gravitational acceleration (9.8 m/sΒ² on Earth)
- h = Height or depth of the liquid above the point (in meters)
Hydrostatic pressure is a critical aspect, being the pressure exerted by a liquid at rest due to the weight of the liquid column above. It is affected by the density of the liquid, the depth of measurement, and the gravitational acceleration.
The section describes Pascalβs Law, stating that pressure applied to an enclosed fluid is transmitted undiminished throughout the fluid. This principle underlies the functioning of hydraulic systems, such as car brakes and lifts. Furthermore, the relationship between pressure and depth highlights that pressure increases with depth, varying based on liquid densities.
Measurement techniques such as manometers are also introduced, along with Archimedesβ Principle, explaining buoyant forces and practical applications. Overall, this section provides a robust understanding of how pressure operates within liquids, relevant for students of fluid mechanics and related fields.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Pressure in Liquids
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
What is Pressure in Liquids?
Pressure in a liquid is the force exerted by the liquid per unit area. It depends on the depth of the liquid, its density, and the gravitational acceleration acting on it.
Pressure in a liquid increases with depth due to the weight of the liquid above the point where pressure is being measured.
Formula for Pressure in a Liquid
The pressure at a point in a liquid is given by the formula:
P = Οgh
Where:
- P = Pressure at a point in the liquid (in Pascals, Pa)
- Ο = Density of the liquid (in kg/mΒ³)
- g = Gravitational acceleration (approximately 9.8 m/sΒ² on Earth)
- h = Height or depth of the liquid above the point (in meters)
Units of Pressure
The SI unit of pressure is the Pascal (Pa), which is defined as one Newton per square meter (1 Pa = 1 N/mΒ²).
Detailed Explanation
Pressure in liquids refers to the force that the liquid exerts on a particular area. It is determined by three main factors: the depth at which the pressure is measured, the density of the liquid, and the gravitational force acting on that liquid. As you go deeper into a liquid, the pressure increases because of the weight of the liquid that is above that point. The relationship is mathematically expressed by the formula P = Οgh, where P is the pressure, Ο is the liquid's density, g is the gravitational pull (around 9.8 m/sΒ²), and h is the depth from the surface of the liquid to the point of measurement. The standard unit used to measure this pressure is the Pascal (Pa), which equates to one Newton per square meter.
Examples & Analogies
Imagine you are swimming in a pool. The deeper you go, the more pressure you feel on your body. This pressure comes from the water above you. If you dive down to the bottom of the deep end, the water is pushing down on you more than when you are at the surface, similar to how more books stacked on a table would create more pressure on the table than just one book.
Hydrostatic Pressure
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
What is Hydrostatic Pressure?
Hydrostatic pressure is the pressure exerted by a liquid at rest. It is caused by the weight of the liquid column above the point where the pressure is being measured.
Hydrostatic pressure acts in all directions and increases with depth because the weight of the liquid increases with height.
Factors Affecting Hydrostatic Pressure
- Density of the Liquid: The greater the density of the liquid, the higher the pressure at a given depth.
- Depth of the Liquid: The deeper the point is in the liquid, the greater the pressure.
- Gravitational Acceleration: The stronger the gravitational force, the greater the pressure. On Earth, g=9.8 m/sΒ².
Detailed Explanation
Hydrostatic pressure specifically describes the pressure within a fluid that is not moving. This pressure is due to the weight of the liquid above the point of measurement. Hydrostatic pressure is not uniform; it increases with depth. Three primary factors influence this pressure: liquid density (denser liquids exert greater pressure), liquid depth (deeper points experience more pressure), and gravitational force (stronger gravity results in higher pressure). Essentially, the deeper you go into any liquid, the more weight of the fluid is pressing down on you, thereby increasing the hydrostatic pressure you would feel.
Examples & Analogies
Consider two swimming pools, one filled with regular water and another with a denser liquid like saltwater. If you dive to the same depth in both pools, you will feel more pressure in the saltwater pool, because the saltwater, being denser, exerts more hydrostatic pressure as you go deeper.
Transmission of Pressure in Liquids
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Pascalβs Law
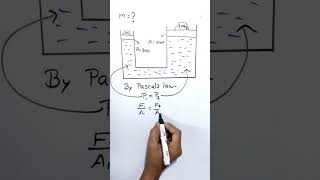
Pascal's Law states that:
'Pressure applied to an enclosed fluid is transmitted undiminished to all parts of the fluid and to the walls of its container.'
Explanation of Pascalβs Law
If a small force is applied to a confined liquid, the pressure in the liquid will be the same at all points, and this pressure will be transmitted equally in all directions.
Applications of Pascalβs Law
- Hydraulic Press: A hydraulic press uses Pascal's Law to amplify the force. A small force applied on a small piston creates a large force on a larger piston.
- Hydraulic Lifts: Hydraulic lifts, used in car repair shops, use Pascalβs Law to lift heavy objects by applying a small force on a small piston, which is transmitted to a larger piston, raising the load.
Detailed Explanation
Pascal's Law explains how pressure in a confined fluid behaves when a force is applied. It implies that changes in pressure applied to the fluid are equally distributed throughout the entire fluid, affecting every part of it uniformly. This principle is essential in hydraulic systems, where a small force applied to a piston can create a much larger force in another piston, which is crucial for devices like hydraulic presses and lifts that we use in daily life for lifting heavy objects with relative ease.
Examples & Analogies
Think of a spray bottle designed to clean windows. When you squeeze the handle, you exert pressure on the trapped liquid. This pressure is transmitted throughout the fluid, causing the liquid to exit the nozzle with great force, allowing you to spray effectively. This is the same principle that allows hydraulic lifts to work; a little pressure from a small pump can lift heavy machinery much higher!
Pressure Variation with Depth in Fluids
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Pressure at Different Depths
As we move deeper into a liquid, the pressure increases. The pressure at a point below the surface of the liquid is proportional to the depth of the point.
Pressure at a Given Depth in Different Liquids
The pressure at a given depth in different liquids depends on their densities. Since water has a density of 1000 kg/mΒ³, the pressure at a given depth in oil (which is less dense) will be lower than in water, and the pressure in mercury (which is denser) will be higher.
Detailed Explanation
The deeper you go into any liquid, the more pressure you will experience due to the weight of the liquid above you. This pressure is directly proportional to the depth, which means that if you go twice as deep, you will feel twice the pressure. However, the type of liquid also mattersβa less dense liquid (like oil) will exert less pressure at a given depth compared to a denser liquid (like mercury). Thus, if you measure pressure at the same depth in different liquids, the readings will differ based on their respective densities.
Examples & Analogies
Imagine being in a swimming pool: if you dive down to the bottom, you feel the weight of the water increasing as you go deeper. On the other hand, if you were to measure pressure in a swimming pool filled with water and then in a fish tank filled with mercury, you'd find that the pressure at the same depth in mercury is much greater, because mercury is denser than waterβjust like how receiving a hug from a big friend feels heavier compared to a hug from a little sibling!
Measuring Pressure in Liquids
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Pressure Measurement Techniques
Manometers are commonly used to measure pressure in liquids. They come in different forms such as U-tube manometers or digital pressure gauges.
- U-Tube Manometer: It consists of a U-shaped tube filled with a liquid (usually mercury or water). The liquid in the tube moves when pressure is applied to one side, and the difference in height is used to calculate the pressure.
Example: Measuring Hydrostatic Pressure Using a Manometer
A U-tube manometer is connected to a container filled with water. The height of the water column in the manometer can be used to calculate the pressure exerted by the water in the container.
Detailed Explanation
Manometers are instruments designed to measure fluid pressure, with U-tube manometers being one of the most traditional forms. These devices consist of a U-shaped tube partially filled with a liquid, such as mercury or water. When pressure is applied to one of the tube's sides, the liquid shifts, and the difference in height between the two sides is measured. This height difference translates directly into pressure using the basic principles of hydrostatic pressure, helping to quantify the pressure exerted by the liquid inside a container.
Examples & Analogies
Think of the manometer as a barometer for liquids. If you ever blown into a straw in a glass of water and seen how high the water level rises, thatβs a simple demonstration of the same principle. Youβre creating higher pressure in the straw that pushes the water up, just like how liquid moves in a U-tube manometer when pressure is applied!
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Pressure increases with depth due to the weight of the liquid above.
-
Pascalβs Law states that pressure applied is transmitted equally in all directions.
-
The buoyant force is equal to the weight of fluid displaced by an object.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
When you dive into a swimming pool, you feel the pressure on your ears increasing as you go deeper.
-
A hydraulic lift, such as those found in car repair shops, uses Pascal's Law to lift heavy vehicles with minimal effort.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
Pressure in the liquid grows, as the depth above it shows.
π Fascinating Stories
-
Imagine you're swimming and going deeper, feeling pressure build around you; itβs like the water is giving you a stronger hug as you submerge, wrapping you tighter, much like how force is transmitted equally around a buoyant object.
π§ Other Memory Gems
-
DDL - Remember Depth, Density, Lift to recall how pressure changes in liquids.
π― Super Acronyms
PULL - Pressure Upward from Liquid Lift describes how the buoyant force works on submerged objects.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Pressure
Definition:
The force exerted by a liquid per unit area.
-
Term: Hydrostatic Pressure
Definition:
The pressure exerted by a liquid at rest due to the weight of the liquid column above.
-
Term: Pascal's Law
Definition:
Pressure applied to an enclosed fluid is transmitted undiminished to all parts of the fluid and to the walls of its container.
-
Term: Buoyant Force
Definition:
The upward force exerted by a fluid on an object submerged in it, equal to the weight of the fluid displaced.
-
Term: Hydrostatic Force
Definition:
The force exerted by a fluid on a surface submerged in it, calculated by integrating pressure over the entire surface.