Numerical Problems on Pressure in Liquids
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Finding Pressure at a Depth
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we'll discuss how we calculate pressure at various depths in liquids. Can anyone tell me the formula for calculating pressure?

Is it P equals density times gravity times height?

Exactly! That's the formula: P = ρgh. Let's apply this by finding the pressure at a depth of 5 meters in water. What is the density of water, and what gravitational acceleration should we use?

The density of water is about 1000 kg/m³, and gravitational acceleration is approximately 9.8 m/s².

Correct! So, substituting these values into the formula, we get P = 1000 * 9.8 * 5. Can anyone calculate that?

It would be 49,000 Pa, or 49 kPa!

Well done! So, at a depth of 5 meters, the pressure is 49,000 Pa. Remember, pressure increases with depth. Let's keep this in mind.
Understanding Buoyant Force
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's move on to buoyant force. Who can tell me what the buoyant force is?

Isn't it the force that pushes objects up when they are in water?

Exactly! It's equal to the weight of the fluid displaced. The formula is F_b = ρVg. If we have a block of wood with a volume of 0.2 m³ floating in water, what would the buoyant force be?

Given the density of water is 1000 kg/m³, we can plug those values into the formula: F_b = 1000 * 0.2 * 9.8.

Great! Can you calculate that?

That would be 1960 N!

Excellent! So, the buoyant force acting on the block is 1960 N. Keep this formula in mind as it will help you with many problems ahead.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we explore key numerical problems that illustrate the concepts of pressure in liquids and buoyant forces, including practical calculations for pressure at specific depths and the buoyant force acting on objects submerged in liquids. Important formulas are applied to enhance problem-solving skills.
Detailed
Detailed Summary
This section provides a comprehensive overview of solving numerical problems related to pressure in liquids. It begins with a foundational understanding that pressure in a liquid is calculated using the formula:
$$ P = \rho g h $$
where \( P \) is the pressure, \( \rho \) represents the liquid's density, \( g \) stands for gravitational acceleration, and \( h \) is the depth of the liquid.
The section then proceeds to offer two key examples to illustrate the application of this formula in practical scenarios:
Example 1 - Finding Pressure at a Depth
This example demonstrates how to calculate the pressure at a depth of 5 meters in water, where the density of water is given as 1000 kg/m³ and gravitational acceleration as 9.8 m/s². The calculations yield a pressure of 49,000 Pa (or 49 kPa).
Example 2 - Buoyant Force Acting on an Object
This example presents a scenario where a block of wood with a volume of 0.2 m³ floats in water. Using the relevant formula for buoyant force:
$$ F_b = \rho V g $$
where \( F_b \) is the buoyant force, the density of water is again taken as 1000 kg/m³. The resulting calculation shows that the buoyant force is 1960 N.
Overall, this section reinforces the importance of understanding the relationships between pressure, depth, and buoyant forces in fluids.
Youtube Videos




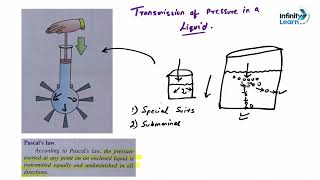


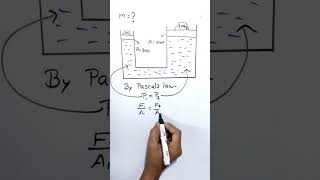
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Example 1: Finding Pressure at a Depth
Chapter 1 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Example 1: Finding Pressure at a Depth
What is the pressure at a depth of 5 meters in water? Given the density of water is 1000 kg/m³, and the gravitational acceleration is 9.8 m/s².
Solution:
P=ρ⋅g⋅h=1000⋅9.8⋅5=49000 Pa
Hence, the pressure at a depth of 5 meters is 49,000 Pa or 49 kPa.
Detailed Explanation
In this example, we calculate the pressure exerted by water at a depth of 5 meters. To find the pressure, we use the formula:
P = ρgh, where P is pressure, ρ (rho) is the density of the liquid (water in this case), g is the acceleration due to gravity, and h is the depth of the liquid.
Plugging in the values, we see that:
- The density of water (ρ) = 1000 kg/m³
- The gravitational acceleration (g) = 9.8 m/s²
- The depth (h) = 5 meters
Thus, we calculate it as follows:
P = 1000 kg/m³ * 9.8 m/s² * 5 m = 49,000 Pa.
Therefore, the pressure at this depth is 49,000 Pa.
Examples & Analogies
Think about diving into a swimming pool. As you go deeper into the water, you feel more pressure on your ears; that’s the increasing water pressure due to the weight of the water above you. Just like we calculated, at 5 meters, the pressure felt is equivalent to 49 kPa, which is noticeable when swimming!
Example 2: Buoyant Force Acting on an Object
Chapter 2 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Example 2: Buoyant Force Acting on an Object
A block of wood with a volume of 0.2 m³ is floating in water. What is the buoyant force acting on the block? Given that the density of water is 1000 kg/m³.
Solution:
Fb=ρ⋅V⋅g=1000⋅0.2⋅9.8=1960 N
Hence, the buoyant force is 1960 N.
Detailed Explanation
This example calculates the buoyant force acting on a floating object, in this case, a block of wood. The buoyant force (Fb) can be calculated using the formula:
Fb = ρVg, where ρ (rho) is the density of the liquid (water), V is the volume of the object submerged, and g is the acceleration due to gravity.
Here, we plug in the values:
- The density of water (ρ) = 1000 kg/m³
- The volume of the wood block (V) = 0.2 m³
- The gravitational acceleration (g) = 9.8 m/s²
Calculating it gives us:
Fb = 1000 kg/m³ * 0.2 m³ * 9.8 m/s² = 1960 N.
Thus, the buoyant force acting on the block of wood is 1960 N.
Examples & Analogies
Imagine placing a small piece of wood in a bucket of water. If you push it down, you'll feel it wanting to push back up—that's the buoyant force in action. The calculation shows that, for this wood block, the force trying to float it back up, due to the water, is 1960 N—similar to feeling the pressure of water pushing back when swimming!
Key Concepts
-
Pressure increases with depth: Deeper points in a liquid experience higher pressure due to the weight of the liquid above.
-
Buoyant force = weight of the fluid displaced: This fundamental principle explains why objects float or sink in a fluid.
Examples & Applications
Calculating pressure at a depth of 5 meters in water gives a result of 49000 Pa.
The buoyant force on a 0.2 m³ block of wood floating in water is calculated as 1960 N.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Pressure grows with every drop, deep in the water, don't you stop!
Stories
As a diver goes deeper into the ocean, he feels the increasing pressure, remembering that the weight of water above him is what is pushing down. Each breath signifies the buoyancy he feels, as the ocean cradles him like a gentle giant.
Memory Tools
To remember the formula for pressure, think 'Pressure Rises with Depth' - PRD (Pressure = Rho * Depth * Gravity).
Acronyms
BFP (Buoyant Force = ρVg) helps recall buoyancy calculations!
Flash Cards
Glossary
- Pressure (P)
The force exerted by a liquid per unit area, measured in Pascals (Pa).
- Density (ρ)
The mass per unit volume of a substance, typically measured in kg/m³.
- Gravitational Acceleration (g)
The acceleration due to gravity, approximately 9.8 m/s² on Earth.
- Buoyant Force (F_b)
The upward force exerted by a fluid on an object submerged in it, equal to the weight of the fluid displaced.
- Volume (V)
The amount of space occupied by an object, measured in cubic meters (m³).
Reference links
Supplementary resources to enhance your learning experience.
