Circle
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Definition of Circle
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Welcome, students! Today we’re discussing circles. A circle is defined as the set of all points that are equidistant from a fixed point, which we call the center. Does anyone know what the fixed distance is called?

Is it called the radius, teacher?

Exactly! The radius is the distance from the center to any point on the circle. Now, remember this acronym: 'CRAP' – Center, Radius, All Points. It captures the essence of a circle. Can anyone explain why the center is crucial in a circle?

The center is significant because it helps us locate other points on the circle!

Great point! The center indeed acts as a reference for defining the circle’s entire structure.
Standard Equation of a Circle
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

"Now, let’s talk about the equation of a circle. The standard equation is
Properties of Circles
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's explore some intriguing properties of circles. One of the key properties is their symmetry. Who can tell me what this means?

It means any diameter divides the circle into two equal halves!

Exactly! Circles are perfectly symmetrical. Another property is the constant radius. What does this imply?

No matter where you measure it from the center, the radius remains the same!

Well said! This consistency is fundamental in ensuring that all points on the circle are equidistant from the center. We'll use these properties as we dive deeper into conic sections.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we delve into the definition, equation, and properties of circles, highlighting their fundamental characteristics such as symmetry and constant radius.
Detailed
Circle
A circle is a fundamental geometric shape defined mathematically as the set of all points that remain an equal distance from a single point known as the center. The distance from the center to any point on the circumference is referred to as the radius. The standard equation representing a circle with center
(h, k) and radius r is given by
(x−h)² + (y−k)² = r².
This equation is crucial in analytic geometry as it establishes the relationship between the coordinates of points on a circle and its center and radius. Circles possess distinct properties, including:
- Symmetry about the center, ensuring every diameter divides it into two equal halves.
- A constant radius which remains the same no matter the position of points on the circumference.
- A geometric definition associated with distance from a central point.
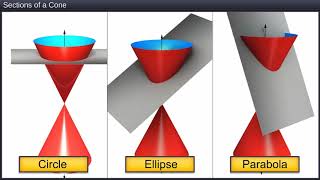
Understanding these attributes is vital, as circles form the basis for exploring other conic sections such as parabolas, ellipses, and hyperbolas.
Youtube Videos




Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of a Circle
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
A circle is the set of all points equidistant from a fixed point called the center. The fixed distance is called the radius.
Detailed Explanation
A circle can be understood as a shape that is completely symmetrical around a point known as the center. Each point on the boundary of the circle is at an equal distance from this center point. This equal distance is referred to as the radius. For example, if you have a circle with a center at point (h, k) and a radius of r, any point on the circle will be exactly r units away from (h, k).
Examples & Analogies
Think of a circle as a round pizza. The center of the pizza is where the toppings are concentrated, and if you measure from the center to any point on the crust (the edge), you will always get the same distance—which represents the radius of the pizza.
Standard Equation of a Circle
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The equation of a circle with center (h, k) and radius r is: (x−h)²+(y−k)²=r².
Detailed Explanation
The standard form of the equation of a circle provides a mathematical way to describe the circle. The equation (x − h)² + (y − k)² = r² shows that for any point (x, y) on the circle, the distance from the point to the center (h, k) is equal to the radius r. By squaring the differences (x-h) and (y-k), we ensure that we are accounting for all points around the center, thus depicting the circle accurately.
Examples & Analogies
Imagine you're standing at the center of a circular playground. If you walk straight outwards in any direction for the same distance each time (your radius), you'll always end up at the edge of the playground—this is similar to how the equation defines all points (x, y) that are at distance r from the center.
Properties of a Circle
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Important properties include symmetry about the center, constant radius, and the geometric definition using distance.
Detailed Explanation
Circles possess several key properties that make them unique. First, they are symmetric about their center, meaning if you draw a line through the center, the two halves will mirror each other. Additionally, a circle has a constant radius, ensuring consistency in distance from the center to any point on the edge. The geometric definition, which involves the concept of distance, illustrates how any point (x, y) fits into the overall structure of the circle.
Examples & Analogies
Consider a perfectly round clock. When you look at it, no matter how you divide it or which angle you look from, each half will look the same because of its symmetry. Additionally, every tick mark that represents the hours is the same distance from the center, just like the points on a circle.
Key Concepts
-
Circle: A set of points equidistant from a fixed point.
-
Center: The fixed point of a circle.
-
Radius: The distance from the center to the circle's circumference.
-
Standard Equation: Mathematical representation of a circle.
-
Symmetry: The property that ensures equal division in a circle.
Examples & Applications
Example 1: A circle with center (2, 3) and radius 4 can be represented by the equation (x−2)² + (y−3)² = 16.
Example 2: If a circle is centered at the origin (0, 0) with a radius of 5, its standard equation is x² + y² = 25.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In a circle so round and neat, all points are equidistant, a real treat!
Stories
Imagine a town where every house is exactly 4 blocks away from the town center. No matter where you stand, if you walk 4 blocks away, you'll find a home. This is how a circle is formed – a perfect path around its center.
Memory Tools
Remember 'CRAP' for Circle's key components: Center, Radius, All Points.
Acronyms
CIRC – Circle
Its Radius is Constant.
Flash Cards
Glossary
- Circle
A set of all points in a plane that are equidistant from a fixed central point.
- Center
The fixed point from which every point on the circle is equidistant.
- Radius
The distance from the center of the circle to any point on its circumference.
- Standard Equation
The mathematical representation of a circle in the form (x−h)² + (y−k)² = r².
- Symmetry
A property where a shape can be divided into two identical parts.
Reference links
Supplementary resources to enhance your learning experience.
