Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Conic Sections
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Good morning, class! Today, we will explore conic sections. Can anyone tell me what conic sections are?
Are they the curves you get when you slice a cone with a plane?
Exactly! Conic sections are formed by the intersection of a plane and a double-napped cone. They include circles, parabolas, ellipses, and hyperbolas. Each of these shapes has distinct properties.
Why are they important?
Great question! They apply to various fields like physics and engineering. We'll learn how to identify them and use their equations in analytic geometry.
So, are the equations of these shapes different?
Yes, each conic section has its own standard equation, which is crucial for graphing them accurately.
Can you give an example of a real-world application?
Certainly! Parabolas, for example, are seen in satellite dishes and bridges due to their unique reflective properties. Understanding their geometry allows engineers to design structures effectively.
That sounds interesting! How do we start calculating these shapes?
We will begin with circles in our next session, where we will delve into their standard equations and properties.
To summarize today, conic sections are essential curves in geometry derived from a cone's intersection with a plane, vital for various scientific applications.
Types and Properties of Conic Sections
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Welcome back! Now that we know about conic sections as a whole, let's look at the four specific types. Who remembers what they are?
Circles, parabolas, ellipses, and hyperbolas!
Right! Each type has its special properties. For instance, circles are defined by their constant radius. Can anyone tell me what characterizes a parabola?
It's the set of points equidistant from a point called the focus and a line called the directrix!
That's correct! And ellipses are defined by the sum of distances from two foci being constant, while hyperbolas are characterized by the difference of distances. Understanding these definitions will help us predict their properties.
So, the properties sound like a lot to memorize.
It can seem that way, but hereβs a trick: use acronyms like 'CEPH' for Circle, Ellipse, Parabola, Hyperbola. This helps you recall the types easily!
What about their equations?
Good point! Each conic has a standard form equation that encapsulates its properties, and we will explore these equations in detail.
In summary, the four types of conic sectionsβcircle, parabola, ellipse, and hyperbolaβhave distinct characteristics that we will learn to describe mathematically.
Applications of Conic Sections
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, let's talk about the applications of conic sections. Can anyone think of examples where they are used?
I read that parabolas are used in satellite dishes!
Exactly! Their reflective properties allow signals to be focused at a single point, improving communication. What about ellipses?
Ellipses are used in orbits of planets!
Correct! The paths of celestial bodies are ellipses. This relationship is crucial for understanding astronomical phenomena.
And circles are found in wheels, right?
Absolutely! Circles play a critical role in any design involving rotation. And hyperbolas can model things like sound waves.
I see! So, knowing about these helps in real-world contexts.
Yes, knowing where and how these shapes apply helps solidify our conceptual growth in geometry. To recap, weβve seen that conic sections are not just theoretical but essential in practical applications across various fields of science and engineering.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section introduces conic sections, detailing the specific types that arise from intersecting a cone with a plane, emphasizing their unique properties and algebraic representations. Understanding these concepts lays the groundwork for further studies in coordinate geometry.
Detailed
Introduction to Conic Sections
Conic sections are a vital aspect of geometry that includes mathematical curves formed by the intersection of a plane with a double-napped cone. Depending on the angle of the plane's intersection, four principal types of conic sections arise: circles, parabolas, ellipses, and hyperbolas. Each of these types has unique properties and algebraic representations, which are essential for the study of analytic geometry.
The significance of understanding conic sections lies in their widespread applications in various fields such as physics, engineering, and computer graphics, among others. By exploring the definitions, equations, and properties related to each type of conic section, students gain foundational knowledge that will enhance their mathematical comprehension and problem-solving skills.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of Conic Sections
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
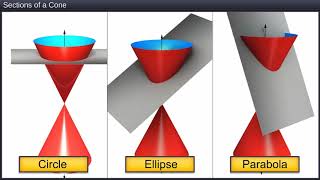
Conic sections are important curves in geometry obtained by slicing a right circular cone with a plane at various angles.
Detailed Explanation
Conic sections arise when a plane intersects with a double-napped cone. Depending on the angle of the slice, different shapes are produced, including circles, parabolas, ellipses, and hyperbolas. Each shape has its own unique properties and equations that define it.
Examples & Analogies
Think of conic sections like different slices of a cake. If you cut straight down, you get a circle (like cutting through the layers). If you cut at an angle, you might see an ellipse or a parabola, just like slicing a carrot at various angles yields different shapes.
Importance of Conic Sections
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Each conic has unique properties and algebraic representations that are fundamental to coordinate geometry.
Detailed Explanation
The study of conic sections is crucial in mathematics, especially in the field of coordinate geometry. Understanding their properties helps in graphing their equations and solving equations related to these curves, which are applicable in various areas such as physics, engineering, and computer graphics.
Examples & Analogies
Imagine youβre designing a roller coaster. Knowing how to work with parabolas and circles helps you design curves that are safe and thrilling. The properties of conic sections guide you in these designs just like a recipe guides you in cooking.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Intersection of a Plane with a Cone: Conic sections are formed by slicing a cone with a plane at various angles.
-
Types of Conic Sections: There are four main types: circles, parabolas, ellipses, and hyperbolas, each with unique properties.
-
Applications: Conic sections appear in many real-world scenarios such as physics, engineering, and computer graphics.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A circle with center at (0,0) and radius 5 can be represented by the equation x^2 + y^2 = 25.
-
The trajectory of a ball thrown in the air typically forms a parabolic path.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
A circle is round, a perfect shape, gliding smoothly, like a landscape!
π Fascinating Stories
-
Once in a land where the shapes played, there were four best friends: Circle, Parabola, Ellipse, and Hyperbola. Each had unique traits that made them shine, together they created constructions divine!
π§ Other Memory Gems
-
CPEH - Remember Circle, Parabola, Ellipse, Hyperbola to keep the order straight!
π― Super Acronyms
For remembering the properties - FACES
- Focus
- Axis
- Constancy
- Eccentricity
- Symmetry!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Conic Sections
Definition:
Curves obtained by the intersection of a plane and a double-napped cone, including circles, parabolas, ellipses, and hyperbolas.
-
Term: Circle
Definition:
A set of points equidistant from a fixed point called the center.
-
Term: Parabola
Definition:
The set of points that are equidistant from a fixed point called the focus and a fixed line called the directrix.
-
Term: Ellipse
Definition:
The set of points where the sum of the distances from two fixed points called foci is constant.
-
Term: Hyperbola
Definition:
The set of points where the difference of the distances from two fixed points called foci is constant.