Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding the Focus and Directrix
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're focusing on the properties of a parabola. To start, does anyone know what the focus is?
Isn't the focus the point that defines the curve of the parabola?
Exactly! The focus is a fixed point. And what's the directrix?
It's a line that helps define the parabola too, right?
Correct! The parabola consists of points equidistant from both the focus and the directrix. A simple way to remember this is using the acronym *FD*: Focus and Directrix define the parabola.
Exploring the Axis of Symmetry
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now let's talk about the axis of symmetry. What can you tell me about it?
I think it's a line that goes through the focus and divides the parabola into two equal halves.
Exactly! It's a vertical line that shows how symmetric the parabola is. Can anyone think of why this is useful?
It helps when graphing it and understanding its shape!
Right! The axis of symmetry is crucial for parabola properties and graphing.
Reflective Property
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, who knows about the reflective property of parabolas?
Isnβt it something about how light reflects off the parabola?
Exactly! Any light ray parallel to the axis of symmetry reflects off the surface and passes through the focus. How can this be useful?
Itβs like how satellite dishes work!
Yes, fantastic connection! So, remember, the reflectivity of a parabola is not just math; it has real-world applications!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the fundamental properties of parabolas. A parabola is defined by points that are equidistant from a fixed point known as the focus and a fixed line termed the directrix. We also cover the axis of symmetry and the unique reflective property of parabolas allowing light to converge at the focus.
Detailed
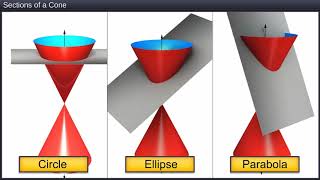
Properties of a Parabola
A parabola is a conic section defined by the set of points that are equidistant from a point called the focus and a line named the directrix. Key properties that characterize parabolas include:
- Focus: The point (a fixed location) around which the parabola curves. All points on the parabola are equidistant from the focus and the directrix.
- Directrix: The fixed line used to define the parabola. The distance from any point on the parabola to the focus is equal to its distance to the directrix.
- Axis of Symmetry: The vertical line that passes through the focus and is perpendicular to the directrix. This line divides the parabola into two mirror-image halves.
- Reflective Property: Parabolas have a unique reflective property where any ray of light parallel to the axis of symmetry, after reflecting off the surface of the parabola, will pass through the focus. This property is critical in applications like satellite dishes and headlights.
Understanding these properties is essential for analyzing parabolas and their applications in real-world scenarios.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Focus and Directrix
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The focus of a parabola is a fixed point, while the directrix is a fixed line. Every point on a parabola is equidistant from the focus and the directrix.
Detailed Explanation
In a parabola, the focus is a specific point located inside the curve, and the directrix is a straight line outside the curve. For any point on the parabola, the distance to the focus is the same as the distance to the directrix. This unique property helps define the shape of the parabola.
Examples & Analogies
Imagine a spotlight shining down on a curved mirror (the parabola); all light rays that hit the mirror and reflect will converge at the focus. The directrix can be thought of as a line on the ground where the light is equally distant from the mirror and the light source.
Axis of Symmetry
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The axis of symmetry of a parabola is a vertical line that passes through the focus and is perpendicular to the directrix.
Detailed Explanation
Every parabola has an axis of symmetry which divides the curve into two identical halves. This line passes through the focus and ensures that for every point on one side, there is a corresponding point on the opposite side at an equal distance from this line.
Examples & Analogies
Think of a seesaw in a playground. If you were to draw a line straight down the middle, both sides would look the same and balance out, just like the left and right sides of a parabola are symmetrical around its axis.
Reflective Property
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
One of the defining properties of a parabola is its reflective property: any ray parallel to the axis of symmetry will reflect off the parabola and pass through the focus.
Detailed Explanation
This property explains how parabolas function in real-world applications like satellite dishes or car headlights. When rays of light (or sound) hit the surface of the parabola, they reflect off in such a way that they all converge at the focus, making parabolas valuable in collecting and directing energy efficiently.
Examples & Analogies
Consider a carβs headlight as a parabola. The light bulb at the focus sends light rays out, and the parabolic reflector ensures that these rays are directed forward in a straight line to illuminate the road ahead.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Focus: The point that defines a parabola's curvature.
-
Directrix: The line used to measure distances to define points on the parabola.
-
Axis of Symmetry: The line that divides the parabola into two identical halves.
-
Reflective Property: The property that allows all parallel rays to converge at the focus after reflection.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A flashlight beam aimed parallel to the axis of a parabolic reflector will converge on the focus, enhancing the light's intensity.
-
A satellite dish is designed in the shape of a parabola to focus signals onto the receiver located at the focus.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
A parabola's shape so divine, focus and directrix both align.
π Fascinating Stories
-
Once a light beam dreamed of shining bright, it found a parabolic mirror, what a sight! A ray so straight, it curved just right, reflecting to the focus, oh so tight!
π§ Other Memory Gems
-
Remember F.D. for Focus and Directrix, the key to finding the parabolaβs tricks.
π― Super Acronyms
To remember parabolic properties
- *F.A.R.* - Focus
- Axis of Symmetry
- Reflective Property.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Focus
Definition:
A fixed point from which distances to points on the parabola are measured.
-
Term: Directrix
Definition:
A fixed line used in the definition of a parabola, from which distances to the focus are calculated.
-
Term: Axis of Symmetry
Definition:
A line that divides the parabola into two mirror-image halves, passing through the focus.
-
Term: Reflective Property
Definition:
The property that states that a ray parallel to the axis of symmetry, upon reflecting off the parabola's surface, will pass through the focus.