Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Definition of Parabola
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're discussing parabolas. A parabola is defined as a set of points that are equidistant from a fixed point called the focus and a straight line known as the directrix.
What does it mean for points to be equidistant from the focus and the directrix?
Great question! It means that for any point on the parabola, if you measure the distance to the focus and the distance to the directrix, those distances will always be equal.
So, does that mean every point on a parabola follows this rule of distance?
Exactly! That's a key characteristic of parabolas. Remember, the focus is crucial for determining the shape of the curve.
Is there a specific formula to describe this?
Yes, we will discuss the standard equation shortly. Just remember that the focus and directrix guide the curve's formation.
To summarize, a parabola consists of all points that maintain equal distance to the focus and directrix.
Standard Equation of a Parabola
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's move to the standard equation of a parabola. The most common form when the vertex is at the origin is $y^2 = 4ax$.
What does 'a' signify in that equation?
'a' represents the distance between the vertex and the focus. If 'a' is positive, the parabola opens to the right; if negative, it opens to the left.
Is this equation applicable to other orientations of parabolas?
Yes! For parabolas opening up or down, the equation changes to $x^2 = 4ay$. Remember that the orientation matters!
How do we find the focus using this equation?
The focus is located at the point $(a, 0)$ for a horizontally oriented parabola. Itβs straightforward once you know 'a'.
To summarize, the standard equation of a parabola $y^2 = 4ax$ describes its shape and orientation based on 'a'.
Properties of a Parabola
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let's dive into the properties of a parabola. They include the focus, directrix, and axis of symmetry.
What role does the axis of symmetry play?
The axis of symmetry divides the parabola into two identical halves. It passes through the vertex and the focus.
What can you tell us about the reflective property of parabolas?
Great point! The reflective property states that any ray parallel to the axis of symmetry will reflect off the parabola and pass through the focus.
Are there practical applications for this reflective property?
Yes, indeed! It's used in satellite dishes and car headlights to direct waves!
In summary, a parabola has a focus, directrix, and an axis of symmetry, along with a unique reflective property, making it very useful in real-life applications.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section explores the definition of a parabola as well as its standard equations and key properties, including its focus, directrix, and reflective characteristics, providing crucial insights into its geometric interpretations and applications.
Detailed
Parabola
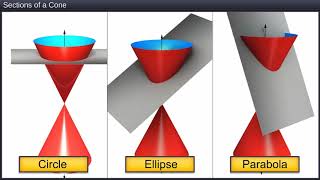
A parabola is a conic section formed by the intersection of a plane and a double-napped cone, defined mathematically as the set of points that are equidistant from a fixed point known as the focus and a fixed line called the directrix.
Standard Equation of a Parabola
For a parabola that opens upwards or downwards with its vertex at the origin, the standard equation is given by:
$$y^2 = 4ax$$
Here, 'a' represents the distance from the vertex to the focus. When 'a' is positive, the parabola opens to the right; when 'a' is negative, it opens to the left.
Properties of a Parabola
Key properties include:
1. Focus: The point that defines the distance that all points on the parabola maintain from the directrix.
2. Directrix: A line that is used in defining the parabola's points.
3. Axis of symmetry: A line that divides the parabola into two mirror-image halves.
4. Reflective property: Any ray parallel to the axis of symmetry reflects off the surface of the parabola and passes through the focus.
This section emphasizes that understanding parabolas is essential, not just in mathematics but also in physics and engineering, where they appear in trajectories, optics, and more.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of a Parabola
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A parabola is the set of points equidistant from a fixed point called the focus and a fixed line called the directrix.
Detailed Explanation
A parabola is a type of curve that can be found in many contexts, such as the path of a thrown object or the shape of satellite dishes. The definition states that a parabola is formed by all points that are the same distance from a fixed point, known as the focus, and a fixed line, called the directrix. To better understand this concept, picture a point moving in such a way that its distance from the focus and the directrix remains equal. This constant distance creates the distinctive U-shape of the parabola.
Examples & Analogies
Imagine a flashlight beam concentrated on a wall; if the light source is point-like and the wall is perfectly flat, the beam will spread out in a parabolic shape. In this way, the focus acts as the point where light is emitted, and the wall represents the directrix.
Standard Equation of a Parabola
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For a parabola with vertex at the origin and focus on the x-axis, the equation is: y^2 = 4ax.
Detailed Explanation
The standard equation of the parabola provides a mathematical framework to describe its shape and position. When the vertex (the tip of the U shape) is at the origin (0,0) and the focus lies on the x-axis, the equation 'y^2 = 4ax' can be used. Here, 'a' represents the distance from the vertex to the focus. If 'a' is positive, the parabola opens to the right, and if 'a' is negative, it opens to the left. This equation allows us to graph the parabola and understand its orientation.
Examples & Analogies
Consider a water fountain; the water shooting up creates a parabolic arc as it falls back down. The focus could be considered the point where water is strongest when it first shoots upward, and the vertex is the lowest point of the fountain's overall height, aligning with the origin of the graph.
Properties of a Parabola
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Focus, directrix, axis of symmetry, and the reflective property.
Detailed Explanation
Parabolas have several significant properties. The focus is a key point that helps define the parabola, while the directrix is the line used in the definition of the curve. The axis of symmetry is an imaginary vertical line that cuts the parabola into two mirror-image halves, located exactly halfway between the focus and directrix. Additionally, parabolas exhibit a reflective property, meaning that light rays parallel to the axis of symmetry will reflect off the surface and pass through the focus. This characteristic makes parabolas important in fields like optics and satellite dishes.
Examples & Analogies
Think of how a parabolic mirror works in a car's headlights. The light bulbs are situated at the focus, and the mirror is designed so that light rays emitted parallel to the axis will reflect off the mirror surface to create a focused beam of light. This is practical in guiding the car, thanks to the parabola's unique reflective properties.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Definition of Parabola: A parabola is defined as the set of points equidistant from a focus and a directrix.
-
Standard Equation: The standard equations are $y^2 = 4ax$ for horizontal and $x^2 = 4ay$ for vertical parabolas.
-
Properties: Key properties include the focus, directrix, axis of symmetry, and reflective property.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Find the focus of the parabola represented by the equation $y^2 = 16x$. Here, 'a' is 4, thus the focus is located at (4, 0).
-
If the directrix of a parabola is given as $x = -2$, find the equation of the parabola that opens to the right and has its vertex at the origin. Answer: $y^2 = 8x$.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
A parabola's a curve so neat, / Focus and directrix make it complete.
π Fascinating Stories
-
Imagine a brave knight whose goal is to find his way from the focus to the directrix. No matter how he moves, he always arrives at a point on the enigmatic curve known as the parabola, forever balancing between these two waypoints.
π§ Other Memory Gems
-
For the parabola, remember 'FAD' - Focus, Axis of symmetry, Directrix.
π― Super Acronyms
P.F.A.R. - Parabolaβs Focus, Axis, Reflection property.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Parabola
Definition:
A conic section defined as the set of all points equidistant from a focus and a directrix.
-
Term: Focus
Definition:
The fixed point from which distances to the parabola are measured.
-
Term: Directrix
Definition:
The fixed line used in conjunction with the focus to define a parabola.
-
Term: Axis of Symmetry
Definition:
The line that divides the parabola into two identical halves.
-
Term: Standard Equation
Definition:
The algebraic representation of a parabola, usually expressed in the form $y^2 = 4ax$ for a horizontal parabola.
-
Term: Reflective Property
Definition:
The property that states that rays parallel to the axis of symmetry reflect through the focus.