Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Conic Sections
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're discussing conic sections, which are the curves we obtain by slicing a double-napped cone with a plane. Who can tell me why these shapes are important?
Are they used in real-life applications?
Absolutely! Conic sections appear in engineering, physics, and even astronomy. For instance, orbits of planets can often be modeled as elliptical shapes. It's vital to understand the unique properties each type of conic section has.
What types of conic sections are there?
Great question! We mainly discuss circles, parabolas, ellipses, and hyperbolas. Each has its own distinctive properties and equations. Let's explore their specifics one by one.
Exploring the Circle
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
First up is the circle. Can anyone define what a circle is?
It's all the points that are the same distance from the center point!
Exactly! And the distance from the center to any point on the circle is called the radius. The standard equation for a circle is (x-h)Β² + (y-k)Β² = rΒ². Can someone explain what (h,k) represents?
(h, k) are the coordinates of the center of the circle!
Correct! Remember, circles are symmetric about their center and always have a constant radius. Let's summarize: circles are defined by their center coordinates and radius, with a specific equation to guide us.
Understanding the Parabola
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Next, we have parabolas. A parabola consists of points equidistant from a focus and a directrix. Can anyone tell me its standard equation when the vertex is at the origin?
Is it yΒ² = 4ax?
That's right! The focus is key to defining the shape of the parabola, and it has a reflective propertyβwhat does that mean?
It means that any ray parallel to the axis of symmetry will reflect through the focus.
Well explained! So remember, the focus, directrix, and symmetric axis are all vital components of a parabola. Letβs move on to the ellipse.
Delving into the Ellipse
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, what is an ellipse? Who can define it for me?
An ellipse is a set of points where the sum of distances from two foci is constant.
Perfect! The standard equation for an ellipse centered at the origin with its major axis along the x-axis is xΒ²/aΒ² + yΒ²/bΒ² = 1. What do a and b represent?
a is the distance to the vertices along the x-axis and b is along the y-axis.
Exactly! The ellipse has a larger semi-major axis and a smaller semi-minor axis. Also, the eccentricity is a measure of how 'stretched' the ellipse is. Let's summarize this section before we discuss the hyperbola.
Examining the Hyperbola
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Lastly, we discuss hyperbolas. What defines a hyperbola?
Itβs the set of points where the difference in distances from two foci is constant!
Correct! The standard equation of a hyperbola centered at the origin with a transverse axis along the x-axis is xΒ²/aΒ² - yΒ²/bΒ² = 1. What does this tell us about the hyperbola's shape?
It has two branches that open away from each other!
Exactly! Each hyperbola has important properties, including its foci, transverse and conjugate axes, and asymptotes. To recap, weβve looked at all four types of conic sections and their equations.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This chapter delves into the definitions, equations, and properties of various conic sections, including circles, parabolas, ellipses, and hyperbolas. Each conic has unique characteristics and equations, fundamental to understanding analytic geometry.
Detailed
Detailed Summary
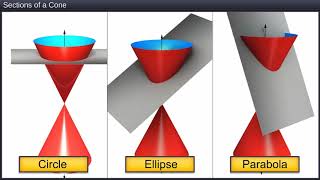
Conic sections arise from the geometric relationship between a plane and a double-napped cone, resulting in different types of curves:
1. Circle: Defined as the set of all points equidistant from a center, with the standard equation given as (xβh)Β²+(yβk)Β²=rΒ². Important properties include symmetry and a constant radius.
2. Parabola: Comprised of points equidistant from a focus and a directrix, represented by the equation yΒ²=4ax when vertex is at the origin. Key properties include its focus, directrix, and reflective characteristics.
3. Ellipse: The collection of points where the sum of distances to two foci is constant, with its standard equation expressed as xΒ²/aΒ² + yΒ²/bΒ² = 1. Essential features include foci, major and minor axes, and eccentricity.
4. Hyperbola: The set of points where the difference in distances from two foci is constant, expressed by the equation xΒ²/aΒ² - yΒ²/bΒ² = 1. Its characteristics include foci, transverse and conjugate axes, and asymptotes.
These conic sections hold significant importance in both pure and applied mathematics, particularly in fields like physics and engineering.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Conic Sections
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Conic sections are important curves in geometry obtained by slicing a right circular cone with a plane at various angles. Each conic has unique properties and algebraic representations that are fundamental to coordinate geometry.
Detailed Explanation
Conic sections arise when a plane intersects a cone. Depending on the angle of the intersection, the resulting shape can be different: a circle, parabola, ellipse, or hyperbola. Each of these shapes has distinct characteristics and formulas that help us understand their properties better.
Examples & Analogies
Think of conic sections like the different shapes of slices you get when cutting a loaf of bread at different angles. A straight cut (horizontal) gives you a circle, a diagonal cut gives you an ellipse, and a curved cut can result in a hyperbola.
Circle
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A circle is the set of all points equidistant from a fixed point called the center. The fixed distance is called the radius.
Detailed Explanation
A circle can be defined mathematically as the collection of all points that are a constant distance (called the radius) away from a central point. The concept of equidistance is what gives the circle its round shape. This definition is fundamental in understanding how circles behave and how they relate to other geometric shapes.
Examples & Analogies
Imagine a clock face. The center of the clock is the focal point, and the hour marks are located at equal distances from this center, forming a perfect circle. The time on the clock represents different points on the circle.
Standard Equation of a Circle
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The equation of a circle with center (h,k) and radius r is:
(xβh)Β²+(yβk)Β²=rΒ²
Detailed Explanation
The standard equation for a circle provides a way to express its location and size in a coordinate plane. The coordinates (h, k) represent the center of the circle, while 'r' defines how far the circle stretches from the center. By plugging in different values for h, k, and r, you can create circles of various sizes and positions on a graph.
Examples & Analogies
Consider a dartboard where the bullseye is at the center. If you state that the radius is 3 inches, the equation helps you visualize all the points that fall within that circle. Every dart landing within that space is equidistant from the center point.
Properties of a Circle
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Important properties include symmetry about the center, constant radius, and the geometric definition using distance.
Detailed Explanation
Circles have several key properties: they are perfectly symmetrical around their center, meaning that any line drawn through this center divides the circle into two equal halves. Additionally, regardless of where you measure from the center, the radius remains constant. This uniformity is what makes circles a fundamental shape in geometry.
Examples & Analogies
Imagine drawing a perfect circle on a piece of paper using a compass. No matter where you measure from the center, the distance to the edge is always the same. This is the constant radius and symmetry of a circle in action.
Parabola
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A parabola is the set of points equidistant from a fixed point called the focus and a fixed line called the directrix.
Detailed Explanation
The definition of a parabola is based on its geometrical properties. The focus is a special point from which distances are measured, and the directrix is a line used as a reference. Any point on the parabola is equally distant from both the focus and the directrix, resulting in the characteristic U-shape of parabolas.
Examples & Analogies
Think about how a satellite dish is shaped. The dish curves towards the center, where the satellite receiver is located (the focus), and the surface of the dish represents points equidistant from the center to the edge where the directrix would be.
Standard Equation of a Parabola
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For a parabola with vertex at the origin and focus on the x-axis, the equation is:
yΒ²=4ax
Detailed Explanation
This equation describes how a parabola opens and how wide it is. Here, 'a' determines the distance from the vertex to the focus. A larger value for 'a' results in a wider parabola, while a smaller value makes it narrower. Understanding this equation is vital for plotting parabolas accurately in coordinate geometry.
Examples & Analogies
Imagine throwing a ball. The path it takes, when plotted on a graph, resembles a parabola. If you throw the ball harder (a larger 'a'), it takes a wider path; if you throw it softer (a smaller 'a'), it arcs higher and falls steeper, resembling a narrower parabola.
Properties of a Parabola
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Focus, directrix, axis of symmetry, and the reflective property.
Detailed Explanation
Parabolas have distinct properties including a focus point, a directrix, and an axis of symmetry that runs vertically through the vertex. The reflective property means that light rays or sound waves that hit a parabolic surface are reflected towards the focus, which has applications in technology (like satellite dishes).
Examples & Analogies
Think about how a flashlight works. If you put a parabolic reflector behind the bulb, all light rays shine towards a point, providing a focused beam of light. This illustrates how the reflective property of a parabola works in everyday devices.
Ellipse
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
An ellipse is the set of points where the sum of the distances from two fixed points called foci is constant.
Detailed Explanation
An ellipse can be defined as the shape created when the distances from two fixed points (the foci) always add up to the same total. This property results in an oval shape. The further apart the foci are, the more elongated the ellipse becomes.
Examples & Analogies
Think of a racetrack that is oval-shaped. No matter where a runner is on the track, the total distance to two points (the foci) at either end of the track remains constant. This constant distance is what defines the shape of the ellipse.
Standard Equation of an Ellipse
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For an ellipse centered at the origin with major axis along the x-axis, the equation is:
xΒ²/aΒ² + yΒ²/bΒ² = 1
Detailed Explanation
In this standard equation, 'a' and 'b' represent the distances from the center to the vertices of the ellipse along the x and y axes, respectively. This equation helps us identify the ellipseβs orientation and dimensions in a coordinate plane.
Examples & Analogies
Imagine a football (soccer ball) laying on the ground. The shape represents an ellipse, where the longest diameter is the major axis, and the shorter diameter is the minor axis. The mathematical equation allows us to define such an elliptical shape accurately.
Properties of an Ellipse
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Includes definitions of foci, major and minor axes, and eccentricity.
Detailed Explanation
Ellipses have interesting properties: two focal points, major and minor axes (the longest and shortest diameters of the ellipse), and eccentricity, which measures how 'stretched out' the ellipse is. The closer the foci are, the less eccentric the ellipse appears and vice versa.
Examples & Analogies
A real-world example is the orbits of planets around the sun, which are elliptical. The eccentricity of these orbits helps us understand how circular or elongated their paths are, influencing how long they take to complete an orbit.
Hyperbola
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A hyperbola is the set of points where the difference of the distances from two fixed points called foci is constant.
Detailed Explanation
A hyperbola is formed when the difference in distances to two foci remains constant. This results in two separate curves that open oppositely. Similar to ellipses, hyperbolas also have a recognized geometric structure, which is significant in mathematics and science.
Examples & Analogies
Consider the paths of two trains moving in opposite directions on separate tracks. No matter their distance, the space between them represents a constant difference, much like the properties of a hyperbola.
Standard Equation of a Hyperbola
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For a hyperbola centered at the origin with transverse axis along the x-axis, the equation is:
xΒ²/aΒ² - yΒ²/bΒ² = 1
Detailed Explanation
This equation defines a hyperbola where 'a' and 'b' determine the shape and orientation. Understanding this equation allows for the diagramming of hyperbolas accurately within a coordinate plane.
Examples & Analogies
Visualize the reflections from a hyperbolic mirror, which allows light to diverge outward. The equation describes the specific curve where these light paths exhibit the hyperbolic property.
Properties of a Hyperbola
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Properties include foci, transverse and conjugate axes, asymptotes, and eccentricity.
Detailed Explanation
Hyperbolas have distinctive properties: two foci, transverse and conjugate axes which define the hyperbola's shape, asymptotes that guide the curvature, and eccentricity, determining how 'stretched' the hyperbola is. These properties make hyperbolas important in advanced mathematics, especially in applications like navigation and physics.
Examples & Analogies
Imagine how radio signals are transmitted. Hyperbolic shapes are often used in antennas and signal mapping. The unique properties of hyperbolas help provide efficient coverage and ensure strong connection signals across distances.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Conic Sections: Defined by the intersection of a plane with a double-napped cone.
-
Circle: A round shape with the center and a constant radius.
-
Parabola: Defined by a focus and a directrix, reflects light in unique ways.
-
Ellipse: Closed curve where the sum of distances to foci remains constant.
-
Hyperbola: Open curve where the difference of distances to foci remains constant.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A circle centered at (3, 4) with a radius of 5 is represented by the equation (x-3)Β² + (y-4)Β² = 25.
-
An ellipse with a major axis of length 10 and a minor axis of length 6 can be represented by the equation xΒ²/25 + yΒ²/9 = 1.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
For a circle, round and neat, with center where all distances meet.
π Fascinating Stories
-
Imagine a bright arching path, where light reflects, thatβs the parabola's math!
π§ Other Memory Gems
-
For Ellipse: 'Focal points and sum are key, defining an ellipse, youβll see!'
π― Super Acronyms
H.E.L.P (Hyperbola, Ellipse, Line, Parabola) to remember conic sections' names.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Conic Sections
Definition:
Curves obtained by intersecting a plane with a double-napped cone.
-
Term: Circle
Definition:
A set of points in a plane that are equidistant from a fixed point called the center.
-
Term: Ellipse
Definition:
The set of points where the sum of the distances to two foci is constant.
-
Term: Parabola
Definition:
A set of points equidistant from a focus and a directrix.
-
Term: Hyperbola
Definition:
The set of points where the difference in distances from two fixed points, called foci, is constant.