Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Parabolas
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're going to learn about the standard equation of a parabola. Can anyone tell me what a parabola is?
Isn't it the shape of the graph of a quadratic function?
That's right! A parabola is indeed the graph of a quadratic equation. Now, can you think of how we can mathematically represent a parabola?
Does it have something to do with the focus and the directrix?
Exactly! A parabola can be defined as the set of points equidistant from a point called the focus and a line called the directrix. Let's build on that and discuss the standard equation for a parabola.
Standard Equation of a Parabola
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
For a parabola with its vertex at the origin and the focus on the x-axis, the standard equation is yΒ² = 4ax. What does 'a' represent?
Is 'a' the distance from the vertex to the focus?
Correct! 'a' defines how wide or narrow the parabola is. If 'a' is positive, the parabola opens upwards; if negative, it opens downwards.
So, the larger the value of 'a', the wider the parabola?
Exactly! This property is crucial when sketching parabolas. Let's summarize what weβve covered so far!
Properties and Applications of the Equation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we've established the equation, can anyone think of a real-life scenario where parabolas might be important?
What about projectile motion in sports?
Great example! The path of a projectile is often parabolic in nature. Understanding the parameters of the parabola can help in predicting where an object will land.
Are parabolas ever used in architecture?
Absolutely! Parabolic arches are common in structures. They provide great strength and stability. Letβs recap the formulas and concepts we've discussed today.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explains the standard equation for a parabola with its vertex at the origin and the focus on the x-axis, which is given by the formula yΒ² = 4ax. The significance of this equation in understanding parabolas is also discussed.
Detailed
Standard Equation of a Parabola
This section focuses on the standard equation of a parabola, defined as the set of all points equidistant from a fixed point called the focus and a fixed line known as the directrix. Specifically, for a parabola that has its vertex situated at the origin and its focus positioned along the x-axis, the standard equation can be expressed as:
Equation
yΒ² = 4ax
In this equation, a represents the distance from the vertex to the focus and also from the vertex to the directrix. Parabolas exhibit unique geometric and algebraic properties, including a focus and a directrix, both of which guide the shape and orientation of the parabola. Understanding this equation is essential for analyzing parabolas within the broader context of conic sections.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of a Parabola
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A parabola is the set of points equidistant from a fixed point called the focus and a fixed line called the directrix.
Detailed Explanation
A parabola is a U-shaped curve that can be defined using its geometric properties. It consists of all the points that are equidistant from a specific point known as the focus and a specific line known as the directrix. This means that for any point on the parabola, the distance to the focus is the same as the distance to the directrix. This property allows us to graph parabolas accurately.
Examples & Analogies
Imagine throwing a basketball towards a hoop. The path of the ball forms a parabolic shape. The point where the ball reaches its highest point is analogous to the focus of the parabola, while the horizontal line that represents the ground can be thought of as the directrix.
Standard Equation of a Parabola
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For a parabola with vertex at the origin and focus on the x-axis, the equation is: y^2 = 4ax.
Detailed Explanation
The standard form of the equation for a parabola with its vertex at the origin (0,0) is given by yΒ² = 4ax. In this equation, 'a' represents the distance from the vertex to the focus. When 'a' is positive, the parabola opens to the right; if 'a' is negative, it opens to the left. This equation allows us to understand how the parabola is shaped and the direction in which it extends.
Examples & Analogies
Think of a parabolic satellite dish. The vertex is at the bottom of the dish, and the focus is where the receiver is placed. The design of the dish (which can be thought of as representing the parabola) ensures that signals coming from satellites are focused at the receiver. The distance 'a' can represent how deep or wide the dish is constructed.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Parabola: The graphical representation of quadratic equations, defined by a focus and directrix.
-
Standard Equation of a Parabola: For a parabola with vertex at the origin and focus on the x-axis, the equation is yΒ² = 4ax.
-
Parameters: 'a' determines the distance from the vertex to the focus and influences the width of the parabola.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: If a = 1, then the equation of the parabola is yΒ² = 4x. This parabola opens rightward and has its focus at (1, 0).
-
Example 2: If a = -2, then the equation becomes yΒ² = -8x, which opens to the left with focus at (-2, 0).
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
In a parabolic sight, a does show, / Width and height, it makes it grow.
π Fascinating Stories
-
Imagine a ball launched from a cannon, following a path like a smile in the skyβthis arc is parabolic, defining how far and high it flies based on its launch angle and speed.
π§ Other Memory Gems
-
F-D for Focus and Directrix helps remember the defining properties of parabolas: Focus is a point, Directrix is a line.
π― Super Acronyms
P-FD = Parabola - Focus-Directrix relationship defines the shape.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Parabola
Definition:
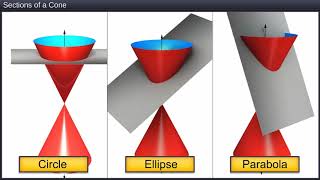
A curve formed by the intersection of a right circular cone and a plane parallel to its side.
-
Term: Focus
Definition:
The fixed point from which distances to points on the parabola are measured.
-
Term: Directrix
Definition:
The fixed line used to define a parabola.
-
Term: Vertex
Definition:
The point where the parabola changes direction; for this equation, it's at the origin.