Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Elementary Row Operations
Unlock Audio Lesson
Today, we will explore elementary row operations. These are methods we use to manipulate matrices while keeping their rank unchanged. Can anyone tell me why this is important?
Maybe because we need to solve equations without changing their solutions?
And if we can change the matrix’s form, it might make solving it easier!
Exactly! By using these operations, we can simplify the process of finding solutions to linear equations. Let's define these operations before we move on to some examples.
Types of Elementary Row Operations
Unlock Audio Lesson
There are three main types of elementary row operations: row swapping, scalar multiplication, and row addition. Who can give me an example of row swapping?
Switching the first row with the second row in a matrix?
Great! Now, scalar multiplication involves multiplying a row by a non-zero number. Can anyone suggest why we can’t multiply by zero?
Because that would make the entire row become zero, and we would lose important information!
Exactly! Now, for row addition, we add or subtract a multiple of one row to another. Let’s practice what we’ve learned with a hands-on example.
Applications of Row Operations
Unlock Audio Lesson
Remember how we talked about Gaussian elimination? Let’s apply our elementary row operations in that context. Who remembers how we can use these operations to reduce a matrix?
By using row operations to eliminate entries below the pivots?
Correct! This process is essential for solving linear systems. Can anyone see where else we could use these operations?
In determining the rank of a matrix, right?
Exactly! Understanding these operations means we can analyze a matrix's rank and its properties effectively.
Practice Exercise
Unlock Audio Lesson
Let's do a quick exercise. I’ll give you a 3x3 matrix, and I want you to apply the row operations to bring it to REF. Ready?
Can we try row swapping first to get a leading 1 on top?
Absolutely! Remember, we can swap rows as needed to position our leading entries correctly. Now, move on to row addition next.
I see how we can simplify the calculations by eliminating lower values!
Summary and Review
Unlock Audio Lesson
Okay everyone, let’s summarize. What are the three types of elementary row operations?
Row swapping, scalar multiplication, and row addition!
Perfect! And why do we use these operations?
To manipulate matrices without changing their rank and to simplify solving systems of equations.
Excellent review! Keep these operations in mind as you continue studying linear algebra.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section discusses elementary row operations, which are essential for converting matrices to row echelon form (REF) or reduced row echelon form (RREF). These operations are pivotal in matrix rank determination and solving linear equations.
Detailed
Elementary Row Operations
In this section, we delve into three primary techniques—row swapping, scalar multiplication, and row addition—that form the foundation for manipulating matrices in linear algebra. These elementary row operations are crucial as they enable the transformation of matrices into Row Echelon Form (REF) or Reduced Row Echelon Form (RREF) without altering their rank.
Key Operations:
- Row Swapping: This operation involves interchanging two rows of the matrix, aiding in the rearrangement of data without loss of information.
- Scalar Multiplication: This entails multiplying all elements of a row by a non-zero scalar, changing the row's values proportionally while maintaining the structure of the matrix.
- Row Addition: This operation involves adding or subtracting a multiple of one row to another. It facilitates the elimination of entries and aids in reaching REF or RREF.
These operations are fundamentally linked to the Gaussian elimination and Gauss-Jordan elimination methods, which are methods used to solve systems of linear equations and find the rank of matrices. Understanding these operations is key for further study in linear algebra and its applications in fields such as engineering.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Elementary Row Operations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
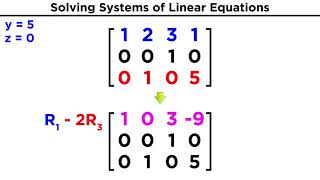
To reduce a matrix to REF or RREF, we use elementary row operations, which do not change the rank of a matrix.
Detailed Explanation
Elementary row operations are essential techniques used in linear algebra to manipulate matrices without affecting their rank. This means that even though we might change the appearance of the matrix, we do not change the information it conveys about linear independence and the solutions to associated systems of equations.
Examples & Analogies
Think of elementary row operations like changing the order of ingredients in a recipe without altering the final dish's taste. Just like rearranging or slightly changing ingredients can lead to the same delicious meal, altering the rows of a matrix in specific ways retains the essential properties of the matrix.
Types of Elementary Row Operations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
These operations are:
1. Row swapping: Interchanging two rows.
2. Scalar multiplication: Multiplying a row by a non-zero scalar.
3. Row addition: Adding or subtracting a multiple of one row to another row.
Detailed Explanation
There are three main types of elementary row operations:
1. Row swapping allows us to change the position of two rows. This is useful to arrange rows to achieve desired formats like row echelon form (REF).
2. Scalar multiplication involves multiplying a row by a non-zero number, which can help simplify the numbers in a matrix for easier calculations.
3. Row addition is where we add or subtract the multiples of one row to another. This helps in eliminating variables when solving systems of equations.
Examples & Analogies
Imagine you are organizing a group of books by swapping their places, changing the number of pages (scalar multiplication), and sometimes adding notes from one book to another (row addition). Each action changes how you look at the books but does not change their fundamental characteristics.
Applications of Elementary Row Operations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
These are used in Gaussian elimination and Gauss-Jordan elimination techniques.
Detailed Explanation
Elementary row operations are crucial in the processes known as Gaussian elimination and Gauss-Jordan elimination. Gaussian elimination transforms a matrix into row echelon form, making it easier to solve systems of equations. Gauss-Jordan elimination takes this a step further to achieve reduced row echelon form, directly revealing the solutions to equations. Both techniques leverage the three types of operations to systematically simplify matrices.
Examples & Analogies
Consider a baker preparing different types of pastries. The process of arranging the ingredients and applying techniques to knead and shape the dough can be likened to elementary row operations. Each method used helps simplify the task of baking, just as row operations simplify matrix forms for solving equations.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Elementary Row Operations: Essential techniques for manipulating matrices without altering their rank.
-
Row Swapping: Interchanging two rows of the matrix to rearrange elements.
-
Scalar Multiplication: Multiplying a row by a non-zero scalar to adjust the row values.
-
Row Addition: Adding or subtracting a multiple of one row to another to simplify the matrix.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
For a matrix A = [1 2; 3 4], swapping rows results in [3 4; 1 2].
-
For matrix B = [2 4, 6; 1 2, 3], multiplying the first row by 2 gives [4 8, 12; 1 2, 3].
-
Performing row addition on C = [1 1; 2 2] by adding twice the first row to the second yields C = [1 1; 4 4].
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Swap and multiply, add to refine, keep your rows in line!
📖 Fascinating Stories
-
Imagine a dance where the dancers swap places (row swapping), a dancer doubles their moves (scalar multiplication), and one dancer helps another learn steps (row addition). This keeps the performance smooth!
🧠 Other Memory Gems
-
SMA: Swap, Multiply, Add to remember the operations.
🎯 Super Acronyms
RSEM
- Remember Swapping
- Scalar
- and Addition in elementary row operations.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Elementary Row Operations
Definition:
Three operations that manipulate rows of a matrix: row swapping, scalar multiplication, and row addition.
-
Term: Row Echelon Form (REF)
Definition:
A form of a matrix where all non-zero rows are above any all-zero rows and leading coefficients of non-zero rows are to the right.
-
Term: Reduced Row Echelon Form (RREF)
Definition:
A further simplified form of a matrix where it is in REF and all leading coefficients are 1, with each leading 1 being the only nonzero entry in its column.