Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Echelon Form
Unlock Audio Lesson
Today, we're going to explore Row Echelon Form, commonly known as REF. Can someone tell me what they think is the significance of reducing a matrix to this form?
I think it helps simplify the matrix, making it easier to understand its properties.
Exactly! By converting a matrix to REF, we can identify the rank by counting the non-zero rows. Now, what do you think is an essential rule for a matrix to be in Echelon Form?
I believe all non-zero rows have to be at the top?
Correct! That's one of the key conditions for REF. Another is that the leading coefficient of each non-zero row must be to the right of the leading coefficient of the row above it. These rules guide us in determining the rank effectively.
Can you give an example of how we find the rank using REF?
Sure! Let's look at a 3x3 matrix. From this matrix, after applying the appropriate row operations, we'll simplify it into REF and then count the non-zero rows to determine the rank.
In summary, reducing a matrix to REF allows us to count the number of non-zero rows, which directly gives us the rank.
Elementary Row Operations
Unlock Audio Lesson
Now, let's delve deeper into the methods we can use to transform a matrix into REF. What are some elementary row operations we can use?
We can swap rows, multiply rows by a non-zero scalar, or add one row to another row, right?
Absolutely! These operations are all essential. Do you remember how each operation affects the rank of a matrix?
I think they don't change the rank, right?
Exactly! The rank stays the same through these operations, which is a key property as it allows us to manipulate the matrix freely without losing its rank. Can anyone tell me why we might want to apply these operations strategically?
To make the leading coefficients clearer and more easily countable?
That's right! It's all about simplification and clarity in the matrix. When we're aiming for REF, the clearer our leading coefficients become, the more effectively we can count non-zero rows.
To summarize, elementary row operations help us transition to REF without altering the rank of the matrix.
Applying Echelon Form to Find Rank
Unlock Audio Lesson
We've covered how to achieve REF. Now let's apply this knowledge to find the rank of a specific matrix. Consider the matrix A we have here. How do we start?
We should apply the necessary row operations to get it into REF!
Exactly! Let's perform a sequence: first, we will subtract two times row 1 from row 2. What do we get?
We get a new second row that has more zeros.
Good observation! And after applying row operations to modify row 3 as well, what do we need to count?
The number of non-zero rows remaining!
I see just one non-zero row, so the rank is 1!
Exactly right! Thus, using Echelon Form, we determined the rank of matrix A is 1. Always remember, the process of reduction simplifies the counting of these non-zero rows.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we learn how to find the rank of a matrix by reducing it to row echelon form through elementary row operations and counting the non-zero rows, highlighting the significance of this method in linear algebra.
Detailed
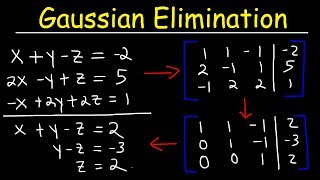
In linear algebra, the rank of a matrix is a crucial concept that indicates the number of linearly independent rows or columns within that matrix, which has profound implications for solving linear systems. This section focuses on Method 1 to determine the rank by transforming a given matrix into Row Echelon Form (REF) using elementary row operations. Once in REF, we can simply count the number of non-zero rows, as this number constitutes the rank of the matrix. For example, given a matrix A, the method shows how through row operations such as row addition, scalar multiplication, and row swapping, we can simplify the matrix to identify its rank efficiently.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
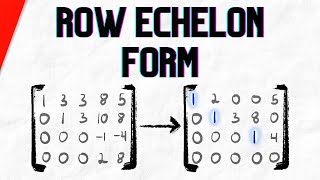
Step 1: Reduce the Matrix to Row Echelon Form
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Reduce the matrix to row echelon form using elementary row operations.
Detailed Explanation
To find the rank of a matrix using this method, the first step is to reduce the matrix to its row echelon form (REF). Row echelon form is characterized by having all non-zero rows above rows of zero, and each leading entry of a non-zero row is to the right of the leading entry of the row above. You can achieve this transformation by applying a series of elementary row operations, which include row swapping, scalar multiplication of rows, and adding/subtracting multiples of one row from another.
Examples & Analogies
Think of organizing a stack of books on a shelf. The goal is to arrange them neatly so that taller books (non-zero rows) are placed in front of shorter ones (zero rows). To achieve this, you might swap positions of books, halve the thickness of thick books, or even combine several thin books into one, making sure they are aligned in a tidy manner!
Step 2: Count the Non-Zero Rows for Rank
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Count the number of non-zero rows; this number is the rank of the matrix.
Detailed Explanation
After reducing the matrix to row echelon form, the next step is to count how many rows contain non-zero entries. The count of these non-zero rows directly gives you the rank of the matrix. This is because each non-zero row represents a linearly independent row vector, contributing to the rank of the matrix.
Examples & Analogies
Imagine you are in a classroom, and the teacher is trying to figure out how many students are actively participating in a discussion. Each student speaking is like a non-zero row—indicating their contribution. If only a few students speak up (the non-zero rows), only their contributions will help in understanding the topic, just as only the non-zero rows contribute to the rank of the matrix.
Example: Echelon Form Applied
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Example: Let
A = [1 2 3]
[2 4 6]
[3 6 9]
Apply row operations:
R → R - 2R
=> [1 2 3]
[0 0 0]
[3 6 9]
R → R - 3R
=> [1 2 3]
[0 0 0]
[0 0 0]
Only one non-zero row remains, so rank = 1.
Detailed Explanation
In this example, we start with matrix A and apply the row operations to reduce it to row echelon form. The first operation changes the second row by subtracting 2 times the first row from it. The resulting rows are assessed, and through further operations, we see that only one row remains non-zero, which indicates the rank of the matrix is 1. The process demonstrates how we can visually observe the reduction process and understand the result regarding the matrix's rank.
Examples & Analogies
Consider this example like a cooking recipe where you are trying to simplify a dish. You start with many included ingredients (the rows), but through the cooking process (row operations), some ingredients become less significant, and you end up with just a few essential flavors (the non-zero rows). Only those remaining flavors that contribute to the dish's taste will count, similar to how non-zero rows contribute to rank.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Row Echelon Form: A matrix form that helps identify non-zero rows efficiently.
-
Elementary Row Operations: Key operations that do not affect the rank during transformation.
-
Rank of a Matrix: Indicates the maximum linear independence among rows or columns.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of transforming a matrix to Row Echelon Form to find its rank by counting non-zero rows.
-
The application of elementary row operations to simplify a matrix for better analysis.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In rows we dig, with zeros we play, the rank will show us the clear way.
📖 Fascinating Stories
-
Once, in a classroom, a matrix transformed using magic row operations, revealing how many independent paths to rank it held.
🧠 Other Memory Gems
-
R-E-F: Rows on top, Each leading is left, Find the zeros, Count what's left.
🎯 Super Acronyms
RER - Reduce, Evaluate, Rank; the simplest steps to determine a matrix's capacity.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Row Echelon Form (REF)
Definition:
A form of a matrix where all non-zero rows are above any rows of all zeros and leading coefficients are ordered from left to right.
-
Term: Rank
Definition:
The maximum number of linearly independent rows or columns in a matrix.
-
Term: Elementary Row Operations
Definition:
Operations that can be performed on the rows of a matrix, including row swapping, scalar multiplication, and row addition.