Method 2: Using Minors
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Minors
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we'll explore how to use minors to find the rank of a matrix. What do you think a minor is, Student_1?

Isn't it some sort of determinant from a smaller piece of the matrix?

Exactly! A minor is the determinant of a square submatrix, which can be derived from the original matrix by removing certain rows and columns. Let's use a simple matrix to demonstrate this.

How do we determine which submatrices to check?

Good question, Student_2! We look at different square submatrices of varying orders. For example, from a 3x3 matrix, we can take 2x2 minors. Each option will help us calculate the determinants.
Finding the Largest Non-Zero Determinant
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, to find the rank, we must identify the largest order of non-zero determinants. Can someone explain how we go about calculating a determinant for a 2x2 matrix?

We multiply the diagonal elements and subtract the product of the other diagonal, right?

Correct! For a minor like \( \begin{bmatrix} 1 & 2 \\ 4 & 5 \end{bmatrix} \), the determinant would be \( (1)(5) - (2)(4) = 5 - 8 = -3 \). It’s non-zero, so we record this!

What if we find several non-zero determinants?

We choose the highest order of any non-zero determinant found. That's the rank of the matrix!
Examples and Practical Applications
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s apply this knowledge to our matrix B from earlier. What did we find when we calculated its determinants?

We found that the 3x3 determinant of matrix B was zero.

But we had a non-zero 2x2 minor!

Correct! This points to the rank of our matrix being 2 due to the presence of that non-zero determinant.

So even if the entire matrix has dependent rows, we can still find a rank!

Absolutely! The use of minors is a powerful method, especially for large or complex matrices.
Summary and Q&A
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

To wrap up, what is the main takeaway when using minors to determine the rank of a matrix?

We need to check the largest non-zero determinant among submatrices!

Exactly! And remember the order of that determinant determines the rank. Any questions or points of confusion?

Can we use this method on any size matrix?

Yes, but the complexity increases with larger matrices since there are more minor combinations. Great question!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we focus on Method 2 for finding the rank of a matrix, emphasizing the process of calculating the order of the largest non-zero determinant from the square submatrices. This offers an alternative approach to understanding matrix rank, particularly useful when the matrix is not in echelon form.
Detailed
Overview of Using Minors to Determine Rank
In linear algebra, determining the rank of a matrix is crucial for understanding its properties and behaviors in various applications. One effective method to ascertain the rank involves finding minors, which are determinants of square submatrices derived from the matrix in question. This section outlines a structured approach to use minors in rank determination as follows:
1. Understanding Minors: A minor of a matrix is defined as the determinant of a square submatrix obtained by removing specific rows and columns. The order of the minor refers to its dimension (e.g., a 2x2 minor from a 3x3 matrix).
- Procedure to Determine Rank Using Minors:
- Identify the order of successive square submatrices.
- Calculate their determinants until reaching the largest non-zero determinant found among these submatrices.
- The order corresponding to this determinant is designated as the rank of the matrix.
-
Illustrative Example: Consider a matrix B:
$$B = \begin{bmatrix} 1 & 2 & 3 \ 4 & 5 & 6 \ 7 & 8 & 9 \end{bmatrix}$$ where the determinant of the full 3x3 matrix equals zero, indicating linear dependence among rows. However, checking the 2x2 minors leads to the identification of a valid non-zero determinant, solidifying the conclusion that the rank of the matrix is 2.
This method is particularly beneficial when working with larger matrices where obtaining echelon form can be cumbersome or impractical.
Youtube Videos



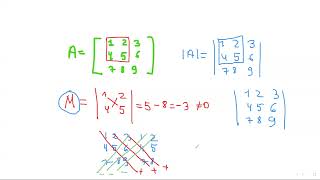






Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Minors
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
- Find the largest order of a non-zero determinant of a square submatrix.
Detailed Explanation
Minors involve identifying smaller square submatrices within a given matrix. The term 'order' refers to the size of these square submatrices. To apply this method, we look for the largest square submatrix whose determinant is non-zero. A determinant being non-zero indicates that the rows or columns of that submatrix are linearly independent.
Examples & Analogies
Think about a team of players in a sport; the larger the team, the more complex it becomes. If you can form a smaller team that works well together (like the submatrix), it shows you have the right mix of players. Thus, finding the 'largest order' corresponds to identifying the biggest effective subgroup.
Order and Rank Connection
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
- The order of the highest such non-zero determinant is the rank.
Detailed Explanation
After identifying non-zero determinants of various square submatrices, we determine their sizes (or orders). The maximum size of these non-zero determinants gives us the rank of the original matrix. This means that the rank reflects the dimension of the vector space spanned by the rows or columns of the matrix.
Examples & Analogies
Imagine you are assessing the performance of different departments in a company. The department that consistently meets targets (with non-zero performance indicators) represents the most effective area of the company. In this analogy, the size of that department reflects its influence or 'rank' within the company structure.
Example in Action
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Example: Let
[1 2 3]
B= 4 5 6
7 8 9
The determinant of the full 3×3 matrix is 0 (since rows are linearly dependent).
Detailed Explanation
In this example, we consider a specific 3x3 matrix. First, we calculate its determinant, which turns out to be zero, indicating that the rows are linearly dependent—meaning one row can be derived from a combination of the others. This tells us that the overall rank of the matrix is less than 3.
Examples & Analogies
Consider the 3x3 matrix as a group project where all members rely on one or two people to perform the tasks. If those key individuals (rows) drop out, the whole project fails (a determinant of 0), and the ability to complete tasks effectively diminishes, reflected in a lower ‘rank’—or capability—of the team.
Finding 2x2 Minors
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now check 2×2 minors. Take:
[1 2]
det =(1)(5)−(4)(2)=5−8=−3≠0
4 5
Detailed Explanation
Next, we examine the 2x2 submatrices of the original matrix. For one such submatrix, we calculate its determinant. Finding a non-zero determinant (in this case, 2x2 minor gives -3) confirms that this smaller submatrix reflects independent rows and columns, contributing positively to the overall rank.
Examples & Analogies
It's like discovering that even though the larger organization struggles, smaller project teams are thriving and independent—demonstrated by their successful completion of smaller tasks (with non-zero outcomes). This independence helps illustrate the capabilities that still exist within the organization.
Conclusion and Rank Derivation
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So rank = 2.
Detailed Explanation
In conclusion, after evaluating the largest square submatrices and finding the highest non-zero determinant order (which was 2 for our previous case), we determine the rank of the matrix to be 2. This signifies that there are 2 linearly independent rows or columns within the original matrix, indicating its effective dimension.
Examples & Analogies
Returning to our project analogy, if your team can only be effective with 2 key members contributing distinctly, then those 2 members represent the rank of the team — giving insight into the strengths of the entire group, even if other members may not provide unique contributions.
Key Concepts
-
Rank: A measure of linear independence within a matrix.
-
Minors: Determinants calculated from square submatrices of a matrix.
-
Determinants: Key arithmetic that helps in understanding the properties of matrices.
Examples & Applications
Example of a 3x3 matrix B where its rank is found using the non-zero determinant of a 2x2 minor.
Example of identifying several minors of various orders and determining the rank of different matrices.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
To find the rank, don’t fret, look for minors, don’t forget!
Stories
Imagine searching for treasures in a matrix; the minors are clues leading to the greatest reward - the rank!
Memory Tools
Remember MINORS: Matrix, Independent, Non-zero, Order, Rank, and Submatrix.
Acronyms
Use 'RANK' for Remembering
Determinants yield the **R**ank by checking for **A**ny **N**on-zero minor **K**eystones.
Flash Cards
Glossary
- Rank
The maximum number of linearly independent rows or columns in a matrix.
- Minor
The determinant of a square submatrix derived from a larger matrix.
- Determinant
A scalar value that can be computed from the elements of a square matrix.
- Submatrix
A matrix formed by deleting one or more rows and/or columns from a larger matrix.
Reference links
Supplementary resources to enhance your learning experience.
