Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Row Echelon Form
Unlock Audio Lesson
Welcome class! Today, we're diving into Row Echelon Form, or REF for short. To start, who can tell me what they think a matrix in REF looks like?
Isn't it the format where all nonzero rows are above the zero rows?
Exactly! That's the first characteristic. Now, can anyone explain the second one?
The leading coefficient of the nonzero rows has to be on the right of the leading coefficient above it, right?
Yes! Very well put! This arrangement helps us easily identify the rank of the matrix. Remember the acronym REF for this, it stands for **Row arrangement**, **Echelon positioning**, and **Form**.
And what about the leading coefficient? Do we need to make it 1 always?
Good question! It’s not mandatory, but setting it to 1 simplifies calculations in reduced forms. Let’s summarize what we covered today about REF: nonzero rows first, leading coefficients in position, and the optional leading 1.
Examples of Row Echelon Form
Unlock Audio Lesson
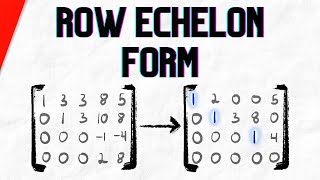
Now, let’s look at some examples. Here’s our first matrix: [1 2 3; 0 1 4; 0 0 0]. Is this in REF?
Yes, because the first row has a leading coefficient followed by zero rows!
Correct! And how about this matrix: [1 3 2; 0 0 5; 0 0 0]?
No, that’s not in REF. The second row has its coefficient out of the leading position.
Yes! Always check for the row positions. Also, remember if you need to clarify something, our acronym LCR helps: **Leading Coefficient**, **Column position**, and **Row order**.
This is helping a lot to visualize things in REF!
Why REF Matters
Unlock Audio Lesson
Why do you think it's essential to convert matrices to REF, especially in engineering fields?
I guess it makes solving equations easier?
Exactly! It simplifies the process to assess the rank, which tells us about linear independence. Can anyone name a context where this is useful?
In civil engineering when analyzing structures, right?
Right again! Remember the acronym RANK: **Reduction**, **Assessment**, **Numerical relationships**, and **Key** applications. This will help aid in remembering its importance.
This is great! I can see how we use these ideas in real-world applications.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section defines Row Echelon Form (REF) and outlines its characteristics, including the arrangement of nonzero rows and leading coefficients. It illustrates how REF is essential for understanding the structure of matrices and solving linear systems.
Detailed
Row Echelon Form (REF)
Overview
In linear algebra, Row Echelon Form (REF) represents a matrix format that simplifies the process of solving linear systems. A matrix is in REF if:
1. All nonzero rows are positioned above any rows of all zeros.
2. The leading coefficient of a nonzero row is strictly to the right of the leading coefficient of the above row.
3. The leading coefficient in each non-zero row is often set to 1, although this is not a strict requirement for REF.
The significance of REF lies in its ability to facilitate matrix rank determination, allowing for a straightforward assessment of linear independence among rows and columns. Understanding REF is crucial for various applications, particularly in structural engineering, where matrix representations are common.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Row Echelon Form
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A matrix is said to be in row echelon form if:
1. All nonzero rows are above any rows of all zeros.
2. The leading coefficient (first non-zero element) of a nonzero row is strictly to the right of the leading coefficient of the row above it.
3. The leading coefficient in any row is 1 (optional for REF).
Detailed Explanation
Row Echelon Form (REF) is a specific arrangement of a matrix that helps us understand its structure. This form has three important rules:
1. Any rows that contain only zeros must appear at the bottom of the matrix. This means that all non-zero rows must come first.
2. The leading coefficient, which is the first non-zero number from the left in a non-zero row, must be to the right of the leading coefficient in the row above it. This establishes a staircase pattern in the matrix.
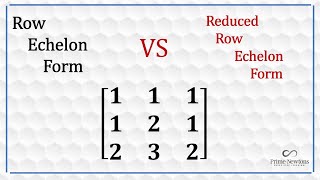
3. Although it is not mandatory, it is often useful for the leading coefficients to be 1. This simplification helps in further calculations like finding the Reduced Row Echelon Form (RREF).
Examples & Analogies
Imagine arranging books on a shelf. You could place thicker books on the bottom (non-zero rows) and get progressively thinner books as you move up. The leading edge of each book (leading coefficient) should start further in from the edge of the book below it, creating a neat staggered effect. This is similar to how non-zero rows should be organized in the Row Echelon Form.
Example of Row Echelon Form
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Example:
[1 2 3]
0 1 4
0 0 0
Detailed Explanation
Let's analyze the provided example of a matrix in row echelon form. The matrix
[1 2 3] [0 1 4] [0 0 0]
has two non-zero rows: the first row has a leading coefficient of 1, and the second row's leading coefficient is also 1, which is correctly positioned to the right of the first row's leading coefficient. The last row is full of zeros, keeping in line with the rule that all non-zero rows must precede the rows of zeros. This structure demonstrates how the rules of REF create a clear and organized representation of the matrix.
Examples & Analogies
Think of this matrix as a team of players where the first two players are in the game (represented by non-zero rows) while the third player is sitting out (represented by the row of zeros). The first player's position '1' is like a captain guiding the second player at '0 1 4', who is strategically placed right behind them with the ball. They are in a formation where no one is blocking them from making a move (the zeros). This structured arrangement helps the coach (us) understand who is playing and their roles.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Row Echelon Form (REF): The organized form of a matrix allowing easy identification of rank.
-
Leading Coefficient: The crucial first non-zero element of a row.
-
Rank: A matrix's rank indicates the number of linearly independent rows or columns.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: Matrix [1 2 3; 0 1 4; 0 0 0] is in REF because it satisfies all conditions.
-
Example 2: Matrix [1 3 2; 0 0 5; 0 0 0] is not in REF due to misplacement of its nonzero row.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Nonzeros on top, coefficients in line, REF makes all matrices divine!
📖 Fascinating Stories
-
Imagine a staircase where every step is a nonzero row leading higher, this stair represents REF leading us to solutions.
🧠 Other Memory Gems
-
Remember LCR for REF: Leading Coefficients, Column right, and rows must be ordered.
🎯 Super Acronyms
REF
- **R**ows **E**mpty on bottom; **F**irst nonzero first!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Row Echelon Form (REF)
Definition:
A form of a matrix where all nonzero rows are above zero rows, leading coefficients of rows are positioned to the right of those above, and leading coefficients are often 1.
-
Term: Leading Coefficient
Definition:
The first non-zero number from the left in a row of a matrix.
-
Term: Linear Independence
Definition:
A property of a set of vectors that cannot be expressed as a linear combination of others in the set.