Rank of a Matrix
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Definition of Rank and Its Importance
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we’ll begin by discussing the rank of a matrix. The rank tells us how many rows or columns in a matrix are linearly independent. Can someone tell me why understanding linear independence is essential?

Isn't it important for solving equations? If the rows or columns aren't independent, it might mean they are redundant.

Exactly! In terms of equations, if we have dependent rows, it can complicate or even prevent us from finding solutions. Remember, the rank can’t exceed the number of rows or columns. It's always less than or equal to the smaller dimension.

So, if I had a 4x3 matrix, the rank could only be 3 or less?

Correct! This brings us to the concept of row rank and column rank. Can anyone tell me if there's a relationship between them?

I think row rank is always equal to column rank, right?

Yes, you're right! This equality is a fundamental property of matrices. Let's summarize: The rank gives us valuable insight into the structure of the matrix, which is crucial in both theoretical mathematics and real-world applications, especially in areas like engineering.
Types of Matrix Forms
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

We've established what rank is. Now, let's delve into Row Echelon Form. A matrix is in REF if all non-zero rows are above the rows of zeros, and the leading coefficient of each non-zero row is to the right of the leading one in the row above. Why do you think this form is useful?

It sounds like it helps in organizing data to find the rank easily.

Absolutely! Once we have a matrix in REF, we can count the non-zero rows to determine the rank. Now, can anyone explain the significance of the leading coefficient being 1?

It might make calculations simpler, right? Like, if you have to perform operations, having a leading 1 is cleaner than having any other number.

Correct! Now, let’s move on to Reduced Row Echelon Form. What distinguishes RREF from REF?

In RREF, each leading entry is the only non-zero entry in its column, making it even easier to interpret.

Exactly right! RREF is more structured and typically easier for interpreting solutions. Let’s summarize: REF helps organize our data, while RREF provides a clearer picture of the solution space.
Elementary Row Operations
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

To achieve REF or RREF, we apply elementary row operations. Can anyone name the three types of operations?

We can swap rows, multiply a row by a scalar, or add/subtract rows.

Correct! And why is it important that these operations do not change a matrix's rank?

Because it ensures consistency in our solutions, right? If the rank doesn't change, the relationships between rows remain the same.

Exactly! This property allows us to transform matrices while still preserving their essential characteristics. Remember, the goal is to simplify and understand the matrix's structure better.

Are these operations the same in Gaussian elimination?

Yes! Both Gaussian elimination and Gauss-Jordan elimination use the same elementary operations to help us derive RREF from REF.
Methods to Find Rank
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

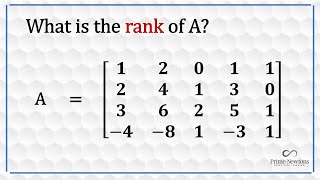
We've covered a lot about definitions and forms. Now let's discuss methods to find the rank of a matrix. What are the two primary methods mentioned?

We can reduce the matrix to Row Echelon Form and count the non-zero rows, or we can look at the determinants of smaller square submatrices.

Exactly! For the first method, can someone walk me through the steps?

We reduce the matrix to REF, then count how many non-zero rows we have. That number gives us the rank.

Great! Now, how about using minors? What’s the procedure there?

We find the largest order non-zero determinant of a submatrix. The order of that determinant is the rank.

Exactly! Both methods are powerful in different contexts, helping us verify our findings. Always make sure to compare results to strengthen your understanding. Let’s summarize our main takeaway: There are multiple ways to find the rank, and the choice of method may depend on the matrix itself.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section delves into the definition, types, methods to find the rank of a matrix, and its applications, particularly in civil engineering. It covers row echelon and reduced row echelon forms, elementary row operations, and the importance of rank in solving linear systems.
Detailed
Rank of a Matrix
The rank of a matrix is an essential concept in linear algebra, providing insight into the matrix's dimensions regarding linear independence. It is defined as the maximum number of linearly independent rows or columns, denoted as rank(A) for a matrix A. The rank offers key information on the solvability of linear systems, the dimensionality of the associated vector space, and much more.
Key Points:
- Definition of Rank: The rank of an m×n matrix A is the maximum number of linearly independent rows or columns, with the fundamental property that rank(A) ≤ min(m, n).
- Matrix Forms: The section discusses Row Echelon Form (REF) and Reduced Row Echelon Form (RREF), illustrating how to simplify a matrix to assess its rank.
- Elementary Row Operations: These are crucial for transforming a matrix while preserving its rank and include operations such as row swapping, scalar multiplication, and row addition.
- Methods to Find Rank: The section explains two primary methods: reducing a matrix to REF and counting non-zero rows or using minors to find the highest non-zero determinant of square submatrices.
- Rank of Special Matrices: Special cases such as zero matrices, identity matrices, diagonal matrices, and triangular matrices are analyzed regarding their ranks.
- Applications in Civil Engineering: The practical implications of rank in linear system solutions, structural analysis, finite element methods, and data interpretation are explored.
- Consistency of Linear Systems: The section discusses the relationship between the rank of the coefficient matrix and the augmented matrix, leading to Rouché–Capelli Theorem implications for solution existence.
Understanding rank is not just a theoretical exercise; it has profound implications across mathematics, engineering, and applied sciences.
Youtube Videos








Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Rank
Chapter 1 of 9
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In linear algebra, matrices are a fundamental mathematical structure used to represent systems of equations, transformations, and data structures. One important concept associated with a matrix is its rank, which provides a measure of the matrix's dimension in terms of linear independence. The rank tells us about the maximum number of linearly independent row vectors or column vectors in a matrix and plays a critical role in solving linear systems, analyzing consistency of equations, and transforming data. In civil engineering, matrices and their ranks are used in structural analysis, finite element methods, optimization problems, and more. A proper understanding of rank helps in checking whether a structure is statically determinate or indeterminate, whether a system of forces is solvable, and in analyzing deformation compatibility equations in structures.
Detailed Explanation
This introduction provides an overview of what a matrix and its rank are in linear algebra. A matrix is a rectangular array of numbers that is used to solve systems of equations, perform transformations, or organize data. The rank of a matrix reflects how many rows or columns consist of unique, independent elements. It is crucial in determining whether linear systems have solutions and the number of those solutions. Additionally, in fields like civil engineering, understanding matrix rank can help analyze structural stability and ensure designs are safe and efficient.
Examples & Analogies
Think of a matrix like a collection of musical instruments in a band. Each instrument contributes a unique sound to the overall performance. The rank of the matrix would be like the number of distinct sounds that add richness to the music. If all instruments were the same (like having multiple identical violins), the band's performance would lack variety, just as a matrix with lower rank has dependent vectors that do not add unique dimensions.
Definition of Rank
Chapter 2 of 9
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The rank of a matrix is defined as the maximum number of linearly independent rows or columns in the matrix. It is denoted by rank(A) for a matrix A. Let A be an m×n matrix. Then, rank(A)=maximum number of linearly independent rows or columns of A. A few important points:
- The rank of a matrix is always ≤ the minimum of its number of rows and columns: rank(A)≤min(m,n).
- Row rank = Column rank, always.
Detailed Explanation
The rank of a matrix quantifies the number of linearly independent rows or columns within it. If you have a matrix with m rows and n columns, the rank cannot exceed the smaller of the two dimensions. This means rank(A) will always be at most equal to the minimum of m and n. Additionally, it is important to note that the row rank (count of independent rows) is equivalent to the column rank (count of independent columns)—this aspect simplifies many calculations because you can analyze either rows or columns and achieve the same conclusion about rank.
Examples & Analogies
Consider a school band with various instruments. If some instruments play the same note, they are not adding unique sounds—just like dependent vectors in a matrix. If the band has 4 violins and only 1 trumpet, the maximum unique sounds (or rank) it can produce is limited to the unique instruments it has, similar to how the rank of a matrix is capped at the lesser number of rows or columns.
Types of Matrix Forms
Chapter 3 of 9
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
(a) Row Echelon Form (REF)
A matrix is said to be in row echelon form if:
1. All nonzero rows are above any rows of all zeros.
2. The leading coefficient (first non-zero element) of a nonzero row is strictly to the right of the leading coefficient of the row above it.
3. The leading coefficient in any row is 1 (optional for REF).
Example:
[1 2 3]
0 1 4
0 0 0
(b) Reduced Row Echelon Form (RREF)
A matrix is in reduced row echelon form if:
- It is in REF.
- The leading entry in each nonzero row is 1.
- Each leading 1 is the only non-zero entry in its column.
Example:
[1 0 2]
0 1 3
0 0 0
Detailed Explanation
The row echelon form (REF) of a matrix organizes its non-zero rows such that all non-zero rows appear above any rows consisting entirely of zeros. Additionally, each successive leading coefficient moves rightward in the rows below, illustrating an ordered structure. The optional requirement for leading coefficients to be '1' allows for flexibility in REF but leads to a stricter form in the case of reduced row echelon form (RREF). RREF specifies not only that the leading coefficients must be '1' but also that they must stand alone in their columns, eliminating any other entries, thus creating a cleaner, more useable format for further analysis.
Examples & Analogies
Imagine organizing a bookshelf. Row Echelon Form is like stacking books in such a way that no empty shelf sections appear above filled sections, and each shelf has books of decreasing height as you go down. Reduced Row Echelon Form takes this a step further, ensuring that every book on a shelf is exactly the same height ('1' metaphorically), and there are no other objects (like paperweights) sharing the same space, making the shelf tidy and functional for quick access.
Elementary Row Operations
Chapter 4 of 9
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
To reduce a matrix to REF or RREF, we use elementary row operations, which do not change the rank of a matrix. These operations are:
1. Row swapping: Interchanging two rows.
2. Scalar multiplication: Multiplying a row by a non-zero scalar.
3. Row addition: Adding or subtracting a multiple of one row to another row. These are used in Gaussian elimination and Gauss-Jordan elimination techniques.
Detailed Explanation
Elementary row operations are fundamental techniques for transforming matrices to row echelon forms while preserving their rank. They include swapping two rows, scaling a row by a non-zero number, and adding or subtracting the multiples of rows. These operations allow for systematic reduction of matrices, making it easier to analyze their properties without altering their fundamental characteristics.
Examples & Analogies
Think of reorganizing furniture in a room. Swapping two chairs, changing the height of a table (scaling), or moving a lamp from one table to another (adding or subtracting) can rearrange the space without changing the essential features of the furniture itself. Similarly, elementary row operations adjust the form of a matrix while keeping its underlying rank intact.
Methods to Find Rank
Chapter 5 of 9
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Method 1: Echelon Form
1. Reduce the matrix to row echelon form using elementary row operations.
2. Count the number of non-zero rows; this number is the rank of the matrix.
Example: Let
[1 2 3]
A= 2 4 6
3 6 9
Apply row operations:
- R →R −2R
2 2 1
- R →R −3R
3 3 1
[1 2 3]
⇒ 0 0 0
0 0 0
Only one non-zero row remains, so rank = 1.
Method 2: Using Minors
1. Find the largest order of a non-zero determinant of a square submatrix.
2. The order of the highest such non-zero determinant is the rank.
Example: Let
[1 2 3]
B= 4 5 6
7 8 9
The determinant of the full 3×3 matrix is 0 (since rows are linearly dependent). Now check 2×2 minors. Take:
[1 2]
det =(1)(5)−(4)(2)=5−8=−3≠0
4 5
So rank = 2
Detailed Explanation
To determine the rank of a matrix, one common method involves converting the matrix to row echelon form and counting the number of non-zero rows. Each non-zero row corresponds to a unique dimension in the context of linear independence. Alternatively, using determinants of square submatrices provides another means of finding rank; the largest non-zero determinant indicates the maximum order of linearly independent rows or columns. This approach highlights the relationships between linear combinations of matrix rows or columns.
Examples & Analogies
Finding rank is akin to determining the variety of flavors in a recipe. Imagine a fruit salad: the unique types of fruit represent linearly independent ingredients. If you can distinguish that you have apples, bananas, and oranges, that represents a rank of 3. If some fruits were duplicates (like having many apples but no other fruit), the distinct flavors you could achieve would be fewer—similar to the independent vectors in a matrix.
Rank of Special Matrices
Chapter 6 of 9
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
(a) Zero Matrix
A zero matrix (all elements 0) has rank 0.
(b) Identity Matrix
The identity matrix of order n has rank n because all rows (and columns) are linearly independent.
(c) Diagonal Matrix
A diagonal matrix with k non-zero diagonal elements has rank = k.
(d) Upper or Lower Triangular Matrix
Its rank is equal to the number of non-zero rows, as they are already in echelon form.
Detailed Explanation
Certain types of matrices have predefined ranks based on their structures. A zero matrix has a rank of 0 because there are no non-zero rows or columns. The identity matrix has a rank equal to its order because all of its rows and columns are independent. Diagonal matrices have ranks equal to the number of non-zero diagonal entries, while both upper and lower triangular matrices have ranks determined by counting non-zero rows, as they already typically exist in an echelon-form structure.
Examples & Analogies
Consider a box of fruits. A box with no fruits (the zero matrix) has a rank of zero because it offers nothing to taste—no independent flavors. A box with one type of fruit, like strawberries (an identity matrix), provides a rank equal to the number of strawberries present. If you have a box filled only with strawberries and some raspberries (a diagonal matrix), your rank increases with additional unique flavors, demonstrating how unique items contribute to the total variety.
Applications of Rank in Civil Engineering
Chapter 7 of 9
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
- Solving Linear Systems Rank determines the consistency of linear systems:
- If rank(A)=rank([A∨B]), the system is consistent.
- If rank(A)=rank([A∨B])=n, the system has a unique solution.
- If rank(A)=rank([A∨B])
Detailed Explanation
The concept of matrix rank extends into practical applications in fields such as civil engineering. For example, the rank is vital in assessing the solvability of linear systems related to structural loads and forces. A consistent system indicates that it can produce valid solutions, while an inconsistent system cannot fulfill its equations, suggesting issues in structural loads or equilibrium. Moreover, in structures, determining whether they are statically determinate or indeterminate relies on the ranks of associated matrices. The use of finite element methods in design also depends on the ranks of global stiffness matrices to assess if structural models function under specified constraints.
Examples & Analogies
Imagine planning a city’s traffic system. Here, ranks are like determining how many routes can successfully transport people to their destinations. If you have many intersections that can be used (higher rank), the routes are viable and there are solutions for navigating traffic. However, if there are problems, like blocked paths or too few alternatives, some routes won’t work, just like inconsistencies in a linear system suggest unsolvable equations in engineering.
Consistency of a Linear System: Rank-Based Approach
Chapter 8 of 9
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Let us consider a linear system of equations:
AX=B
Where:
- A is the coefficient matrix,
- X is the column vector of unknowns, and
- B is the column vector of constants.
The augmented matrix is
[A∨B].
The consistency and solution nature of this system depends on comparing the ranks of A and [A∨B].
Detailed Explanation
In linear algebra, when dealing with a system of equations represented in the form AX = B, where A is a matrix of coefficients, X is a column of variables, and B is a column of constants, the augmented matrix [A|B] helps us analyze the system’s solution. The relationship between the ranks of matrix A and the augmented matrix [A|B] determines whether there are solutions available and if they are unique or multiple. This comparison provides clear insights into the overall behavior of the system.
Examples & Analogies
Consider baking cookies. Your recipe (AX) requires a specific number of ingredients (X). If you have the correct amounts (B) and ingredients are available, you'll achieve the baking result you want. Checking if the ingredients (A) match what’s needed (B) is like checking rank; a proper match means your cookie recipe will work, while mismatches mean you’ll end up with no cookies or too many unworkable combinations.
The Rouché–Capelli Theorem
Chapter 9 of 9
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
A system of linear equations is consistent (i.e., has at least one solution) if and only if rank(A)=rank([A∨B]). If the system is consistent:
- Unique solution if rank(A)=number of variables
- Infinitely many solutions if rank(A)
Detailed Explanation
The Rouché–Capelli theorem establishes a clear rule for determining whether a system of linear equations has any solutions. A consistent linear system has at least one solution, represented when the ranks of matrix A and the augmented matrix [A|B] are equal. Additionally, if the rank of A equals the number of variables, there exists a unique solution. If the rank is less than the number of variables, there are infinitely many solutions. In contrast, inconsistent systems are indicated by differing ranks, implying the absence of any solutions.
Examples & Analogies
Think of a map showing routes to reach different destinations. The Rouché–Capelli theorem works like a guide to ensure you find paths that connect points accurately. If two destinations (A and [A|B]) align, your paths exist (a solution). If one destination has routes that stop short or take you off course (different ranks), then you won't reach your desired location. This analogy highlights how ranks help clarify whether solutions exist in real-world navigation.
Key Concepts
-
Rank: The number of linearly independent rows or columns in a matrix.
-
Row Echelon Form (REF): A matrix form where leading coefficients are positioned in a stair-step configuration.
-
Reduced Row Echelon Form (RREF): Similar to REF but with leading 1's and zeroes in specific positions.
-
Elementary Row Operations: The operations which preserve the rank and alter the matrix towards REF/RREF.
-
Minors: The determinants of square submatrices used to find rank.
-
Applications of Rank: How rank is used in real-world contexts such as solving linear systems.
Examples & Applications
Example 1: For the matrix [1 2; 3 4], rank = 2 because both rows are linearly independent.
Example 2: For the matrix [1 2 3; 2 4 6], rank = 1 because the second row is a multiple of the first.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
If the rows all align, then you will find, the matrix's rank is simply defined.
Stories
Imagine a town where each house represents a row in a matrix. If all houses can be reached from multiple paths, they don't count as unique; this is like linear dependence in ranks.
Memory Tools
Remember 'RCE' for Row operations: R for Row swapping, C for Scalar change, E for Each row addition.
Acronyms
'REF' can stand for 'Rows Excel Framework' to remember Row Echelon Form’s structure.
Flash Cards
Glossary
- Rank
The maximum number of linearly independent rows or columns in a matrix.
- Row Echelon Form (REF)
A form of a matrix where non-zero rows are above the zero rows and the leading coefficient of any row is to the right of the leading coefficient of the row above it.
- Reduced Row Echelon Form (RREF)
A form of a matrix where it is in REF, each leading entry is 1, and each leading 1 is the only non-zero entry in its column.
- Elementary Row Operations
Operations used to modify a matrix that do not alter its rank, which includes row swapping, scalar multiplication, and row addition.
- Minors
Determinants of square submatrices used to determine the rank of a matrix.
- Identity Matrix
A square matrix with ones on the diagonal and zeros elsewhere, which has a rank equal to its size.
- Zero Matrix
A matrix in which all elements are zero, which has a rank of zero.
Reference links
Supplementary resources to enhance your learning experience.
