Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Zero Matrix
Unlock Audio Lesson
Let's start with the zero matrix. Can anyone tell me what a zero matrix is?
Is it a matrix where all the elements are zero?
Exactly! And what can you tell me about its rank?
The rank of a zero matrix must be zero, right?
Correct! A zero matrix does not have any linearly independent rows or columns. Remember, the rank measures the dimension of the matrix in terms of independence.
So, it can't help in solving a system of equations?
That's right! It indicates a lack of direction in vector space. Great job! Summarizing, rank of the zero matrix = 0.
Identity Matrix
Unlock Audio Lesson
Next up is the identity matrix. Who can describe what it looks like?
It has ones on the diagonal and zeros elsewhere!
Correct! Now, what can you tell me about its rank?
The rank should be equal to the number of rows or columns, which is n.
That's right! The identity matrix has full rank because all rows and columns are linearly independent. Remember, for an n x n identity matrix, rank = n.
How does that help in solving linear equations?
Good question! It acts as the multiplicative identity in matrix algebra, facilitating solution processes. Summary: rank of identity matrix = n.
Diagonal Matrix
Unlock Audio Lesson
Now, let’s discuss diagonal matrices. What can you tell me about their structure?
They have non-zero elements only on their diagonal, right?
Exactly! And what would determine their rank?
It would be equal to the number of non-zero diagonal elements.
Correct! This makes it easier to compute their rank for practical calculations. Remember: rank of a diagonal matrix equals the count of non-zero diagonal entries.
Does that mean if all diagonal elements are zero, the rank is zero?
Absolutely! Excellent understanding. To summarize: rank of diagonal matrix = k, where k is the number of non-zero diagonal elements.
Triangular Matrices
Unlock Audio Lesson
Lastly, let’s focus on triangular matrices. What do you know about their structure?
They have only zeros below the diagonal for upper triangular, and only zeros above for lower triangular, right?
Exactly! And how do we determine their rank?
By counting the number of non-zero rows.
Correct! Since triangular matrices are in echelon form, their rank is straightforwardly found by observing non-zero rows. Great discussion! To summarize: rank of triangular matrix = number of non-zero rows.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The rank of special matrices such as zero, identity, diagonal, and triangular matrices is discussed, emphasizing their implications in linear algebra and applications. Each type's rank is defined, and their significance in solving linear equations is highlighted.
Detailed
Detailed Summary
In linear algebra, the rank of a matrix is an essential concept, and certain specialized matrices have specific ranks that are predictable. This section elaborates on the ranks associated with special matrices:
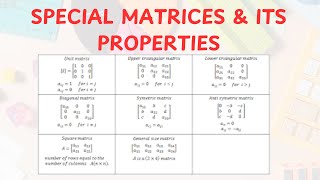
1. Zero Matrix
A zero matrix, which consists entirely of zeros, has a rank of 0 because it does not contain any linearly independent rows or columns.
2. Identity Matrix
The identity matrix of order n has a rank of n, signifying that all its rows and columns are linearly independent. This property facilitates its use as an essential tool in systems of linear equations, particularly in finding solutions and performing transformations.
3. Diagonal Matrix
A diagonal matrix's rank equals the number of its non-zero diagonal elements, indicating how many dimensions contribute to its span in vector space. This rank can also help simplify matrix operations in various applications.
4. Upper or Lower Triangular Matrix
The rank of both upper and lower triangular matrices directly corresponds to the number of non-zero rows in the matrix, as they naturally conform to the echelon form, making it easier to determine their rank through simple observation.
These characteristics underscore the importance of understanding the rank of special matrices, particularly in applied fields like engineering, where they help analyze systems and structures efficiently.
Youtube Videos
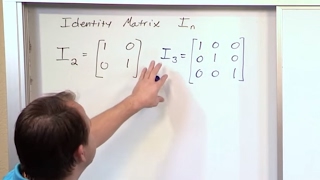
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Rank of Zero Matrix
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A zero matrix (all elements 0) has rank 0.
Detailed Explanation
A zero matrix is a matrix where every entry is zero. Since there are no non-zero rows or columns in a zero matrix, it cannot have any linearly independent rows or columns. Therefore, the rank, which measures the maximum number of linearly independent rows or columns, is 0.
Examples & Analogies
Think of a team with no members, like an empty box. Just as an empty box has no items to show, a zero matrix has no 'independent vectors' to represent. Thus, its rank is zero.
Rank of Identity Matrix
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The identity matrix of order n has rank n because all rows (and columns) are linearly independent.
Detailed Explanation
An identity matrix is a square matrix with 1s on the diagonal and 0s elsewhere. For an identity matrix of order n, each row and column is unique and linearly independent. This means that all n rows (or columns) can be expressed without relying on one another, giving it a rank equal to n.
Examples & Analogies
Imagine a team of n players in a sport, where each player has a unique skill. Each player's skill adds a unique contribution to the team, similar to how each row in an identity matrix adds its own unique contribution. Thus, just like a fully skilled team has n unique players, the identity matrix has rank n.
Rank of Diagonal Matrix
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A diagonal matrix with k non-zero diagonal elements has rank = k.
Detailed Explanation
A diagonal matrix is a matrix where only the diagonal elements (from the top left to the bottom right) can be non-zero, while all off-diagonal elements are zero. The rank is determined by the number of non-zero entries on the diagonal. If a diagonal matrix has k non-zero diagonal elements, this indicates there are k linearly independent rows or columns, hence, the rank is k.
Examples & Analogies
Think of a set of k road signs along a straight road, where each sign represents an important point of information. Only the signs standing upright (the non-zero entries) convey useful direction, just as the non-zero diagonal entries contribute to the matrix's rank. Hence, if there are k signs, the rank is k.
Rank of Triangular Matrices
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Its rank is equal to the number of non-zero rows, as they are already in echelon form.
Detailed Explanation
Triangular matrices can be either upper triangular (where all entries below the main diagonal are zero) or lower triangular (where all entries above the main diagonal are zero). The rank of a triangular matrix is determined by how many rows contain non-zero entries. Each non-zero row corresponds to a linearly independent vector, leading to the conclusion that the rank is equal to the count of non-zero rows.
Examples & Analogies
Consider a staircase where each step represents a non-zero row in a triangular matrix. Each step leads you higher, just like each non-zero row increases the rank of the matrix. If there are three steps (or non-zero rows), the rank is three, providing clear insight into how high you've climbed.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Rank: The maximum number of independent rows or columns in a matrix.
-
Zero Matrix: A matrix consisting entirely of zeros with rank 0.
-
Identity Matrix: A square matrix of ones along the diagonal with full rank equal to n.
-
Diagonal Matrix: A matrix where the rank equals the number of non-zero diagonal elements.
-
Triangular Matrix: The rank equals the number of non-zero rows.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The zero matrix [0 0; 0 0] has a rank of 0.
-
The identity matrix I = [1 0; 0 1] has a rank of 2.
-
A diagonal matrix D = [2 0; 0 3] has a rank of 2.
-
An upper triangular matrix U = [1 2 3; 0 4 5; 0 0 6] has a rank of 3.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a zero matrix, zeros shine, giving rank a value that is just fine: zero for the rank every time!
📖 Fascinating Stories
-
Imagine a party where the hosts, represented by the identity matrix, can greet every guest individually, showing they are all distinct. The party's rank matches the number of guests, highlighting the identity matrix's full rank property.
🧠 Other Memory Gems
-
For diagonal matrices, remember 'K Determinants' where K is the count of non-zero diagonal elements to find the rank.
🎯 Super Acronyms
DAG for Diagonal, All good for remembering that the rank depends on the non-zero diagonal entries.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Rank
Definition:
The maximum number of linearly independent rows or columns in a matrix.
-
Term: Zero Matrix
Definition:
A matrix where all elements are zero, with a rank of 0.
-
Term: Identity Matrix
Definition:
A square matrix with ones on the diagonal and zeros elsewhere, having a rank equal to its order n.
-
Term: Diagonal Matrix
Definition:
A square matrix in which the entries outside the main diagonal are all zero, with rank equal to the number of non-zero diagonal entries.
-
Term: Triangular Matrix
Definition:
A matrix that is either upper or lower triangular, where the rank corresponds to the count of non-zero rows.