Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Eigenvalues
Unlock Audio Lesson
Today we'll dive into the concepts of eigenvalues and eigenfunctions. To start, who can tell me what an eigenvalue represents in our vibrating membrane solutions?
Isn't it like a value that characterizes the behavior of the system at certain frequencies?
Exactly! Eigenvalues help us determine the natural frequencies of vibration. In our case, they take the form of $$\alpha = \frac{n\pi}{a}$$ and $$\beta = \frac{m\pi}{b}$$. Can anyone explain why these values are important?
Because they determine the different modes of vibration?
Correct! Each mode of vibration corresponds to a specific pair of eigenvalues, which we use to build our solution.
So, the higher the n or m, the more complex the vibration pattern?
That's right! Higher eigenvalue pairs indicate more complex vibrational modes.
In summary, eigenvalues are central to understanding how membranes vibrate, and we have to calculate them to find our solutions.
Exploring Eigenfunctions
Unlock Audio Lesson
Now that we know about eigenvalues, let’s talk about eigenfunctions. Can anyone tell me what they are?
Are they the functions that correspond to those eigenvalues?
Correct! Eigenfunctions describe the shape of the vibrations and are defined as $$\phi_n(x) = \sin\left(\frac{n\pi x}{a}\right)$$ and $$\psi_m(y) = \sin\left(\frac{m\pi y}{b}\right)$$. Why do we use sine functions for this?
Sine functions naturally fit the boundary conditions of zero displacement at the edges.
Exactly! The sine functions ensure that the membrane remains fixed at its boundaries while allowing for oscillation. Can you see how we can combine these functions?
Wouldn't we add them together to represent different modes?
Yes! By combining these eigenfunctions, we can represent the overall displacement of the membrane.
Understanding the Total Solution
Unlock Audio Lesson
Let’s piece everything together. Who can summarize how we form the total solution using eigenvalues and eigenfunctions?
We take summations of all the eigenfunctions multiplied by their corresponding coefficients.
"Correct! Our general solution is this superposition:
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explains how eigenvalues (α = nπ/a, β = mπ/b) emerge from the separation of variables method, associating them with specific sine functions that represent eigenfunctions. Each mode of vibration corresponds to a unique eigenvalue pair, contributing to the overall solution.
Detailed
Eigenvalues and Eigenfunctions
In this section, we explore the fundamental concept of eigenvalues and eigenfunctions in regard to vibrating rectangular membranes. When solving boundary value problems with the method of separation of variables, we find that the spatial parts of the solutions yield specific values known as eigenvalues, represented as
$$\alpha = \frac{n\pi}{a} \
\beta = \frac{m\pi}{b}$$
where $n$ and $m$ are positive integers. The corresponding eigenfunctions are given by sine functions:
$$\phi_n(x) = \sin\left(\frac{n\pi x}{a}\right), \
\psi_m(y) = \sin\left(\frac{m\pi y}{b}\right).$$
Each mode of vibration of the membrane corresponds to a unique pair of eigenvalues $(\alpha_n, \beta_m)$, and the complete solution for the displacement of the membrane is represented as a superposition of these modes. This mathematical representation is essential for understanding how the membrane behaves under vibrations, further reinforcing its application in engineering design and analysis.
Youtube Videos
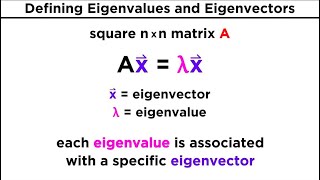
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Eigenvalues Defined
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In the process of solving the boundary value problem using separation of variables, the values α = nπ, β = mπ serve as eigenvalues.
Detailed Explanation
Let's break this down: when we separate the variables in the wave equation, we end up with equations that depend on different variables (x and y). These eigenvalues, α and β, represent specific solutions for the spatial dimensions of the problem. In particular, they correspond to the frequencies of the oscillation modes of the membrane. The values n and m are integers that index these modes, and π is a mathematical constant approximately equal to 3.14. Therefore, each choice of n or m gives a specific eigenvalue that is useful in further computations of the system's behavior.
Examples & Analogies
Think of eigenvalues like different musical notes produced by a musical instrument. Each note corresponds to a specific frequency, just as each eigenvalue corresponds to a specific oscillation frequency of the membrane.
Eigenfunctions Explained
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The corresponding sine functions: ϕ_n(x) = sin(nπx/a) and ψ_m(y) = sin(mπy/b) are eigenfunctions.
Detailed Explanation
Eigenfunctions are specific functions that correspond to each eigenvalue. Here, ϕ_n(x) and ψ_m(y) are sine functions defined for the spatial variables x and y respectively. They describe the shape of the vibration modes of the membrane. Essentially, for each mode defined by n or m, you get a specific sine wave. The sine function is periodic and oscillates between -1 and 1, allowing it to represent the displacement of the membrane accurately over its length and width.
Examples & Analogies
Imagine the waves in a pond when you throw a stone. Each wave represents an eigenfunction. As the stone creates ripples, those ripples travel across the surface of the water in specific patterns; similarly, the eigenfunctions describe the patterns of vibration across the membrane.
Relationship Between Eigenvalues and Modes of Vibration
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Each mode of vibration of the membrane corresponds to a specific eigenvalue pair (α, β), and the total solution is a superposition of all such modes.
Detailed Explanation
In a vibrating membrane, each mode of vibration can be identified by a pair of eigenvalues (α, β). This means that for every unique combination of n and m, there is a unique mode of vibration. The total solution to the vibrating membrane problem can be constructed by combining (or superimposing) all these individual modes. This superposition principle is crucial because it allows us to account for complex vibrations by simply adding together these simpler, base modes.
Examples & Analogies
Consider a group of musicians playing different instruments. Each musician produces a unique sound corresponding to their instrument (akin to eigenvalues), and when they play together, their sounds combine to create a complex piece of music (the total solution).
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Eigenvalues: Scalar values (α = nπ/a, β = mπ/b) corresponding to specific modes of vibration.
-
Eigenfunctions: The sine functions (φ_n(x) and ψ_m(y)) represent displacement modes related to eigenvalues.
-
Superposition of Modes: The total solution for membrane vibration is a summation of various eigenfunctions.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
For n=1, m=1, the fundamental mode of vibration of the membrane shows no internal nodal lines.
-
In the second mode of vibration (n=2, m=1), a nodal line divides the membrane vertically.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Eigenvalues strike with π, natural frequencies on high.
📖 Fascinating Stories
-
Imagine a vibrating membrane, each eigenvalue a note in its refrain. Sine functions dance like light in a lane, defining the mode with perfect gain.
🧠 Other Memory Gems
-
AE (A for Eigenvalues, E for Eigenfunctions) - Remember 'Absolutely Extraordinary' with Eigenvalues and Eigenfunctions.
🎯 Super Acronyms
EVE
- Eigenvalues (E)
- Vibrations (V)
- Eigenfunctions (E).
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Eigenvalue
Definition:
A scalar value that characterizes a particular mode of behavior for a differential operator, resulting in a corresponding eigenfunction.
-
Term: Eigenfunction
Definition:
A function associated with an eigenvalue, representing the shape and mode of vibration of a system.
-
Term: Boundary Value Problem
Definition:
A differential equation together with a set of additional constraints, called boundary conditions, that the solution must satisfy.