Orthogonality of Sine Functions
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Orthogonality
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we'll discuss the orthogonality of sine functions, which is a key concept in Fourier analysis. Can anyone tell me what orthogonality means in the context of functions?

Does it mean that the functions are perpendicular to each other?

That's correct! When functions are orthogonal over an interval, their integral product equals zero. This simplifies analyses in systems like vibrating membranes. Can anyone give an example?

Like when we integrate sin(nx) and sin(mx) over a complete cycle, they end up being zero if n is not equal to m?

Exactly! That's a wonderful insight.
Mathematical Representation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's look at the mathematical expression for this orthogonality. The integral of sin(mx) sin(nx) over the interval from 0 to a. How can we express that?

We integrate the product from 0 to a, and it equals zero for m not equal to n.

Correct! And if m equals n, what does that integral equal?

It equals a divided by 2, right?

Exactly! This property allows us to isolate Fourier coefficients cleanly. Can anyone see why this is beneficial in engineering applications?

It helps in simplifying calculations of vibrations in membranes, since we can treat each mode independently.

Right on! This independence is fundamental for accurate modeling.
Applications of Orthogonality
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s discuss how the concept of orthogonality applies to practical scenarios. Can anyone think of an engineering example?

In analyzing vibrations for bridges or building structures. Each mode can be analyzed separately because of this property.

Exactly! The orthogonality makes it easier to manage complex vibrations by focusing on one mode at a time. What does that allow engineers to do?

They can compute responses to different types of loads more accurately.

Spot on! This ensures safety and reliability in structures. Lastly, can we summarize the importance of orthogonality in our context?

Orthogonality helps in simplifying calculations in Fourier analysis, allowing us to analyze each vibration mode independently.

Perfect summary!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, the orthogonality of sine functions is explored, emphasizing how this property allows for the independent extraction of Fourier coefficients in double Fourier series. This mathematical framework is essential for analyzing the vibrational patterns of rectangular membranes.
Detailed
In this section, we delve into the concept of orthogonality of sine functions, highlighting its importance in deriving Fourier coefficients for the analysis of vibrating rectangular membranes. For integers m, n in natural numbers (N), the orthogonality condition is stated, indicating that the integral of the product of two sine functions over a given interval results in zero if the indices are different, and a non-zero value otherwise. Mathematically, we express this as:
\[ \int_0^a \sin\left(\frac{m\pi x}{a}\right) \sin\left(\frac{n\pi x}{a}\right) dx = \begin{cases} 0, & \text{if } m \neq n \ \frac{a}{2}, & \text{if } m = n \end{cases} \]
A similar condition holds for the variable y over a different interval. This orthogonality ensures that each term in the double Fourier series expansion remains independent, which simplifies the extraction of Fourier coefficients, A_mn and B_mn. This section thus underlines a fundamental aspect of harmonic analysis used in solving boundary value problems in engineering applications like structural vibrations.
Youtube Videos
![[OLD] Haberman 2.3.4 - Orthogonality of sine functions](https://img.youtube.com/vi/S3orVr_oOmI/mqdefault.jpg)






Audio Book
Dive deep into the subject with an immersive audiobook experience.
Orthogonality Concept
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
An essential property used in deriving Fourier coefficients is the orthogonality of sine functions. For integers m,n∈N, we have:
Z a (mπx)(nπx) {0, m≠n
dx=
a
a, m=n
0 2
Detailed Explanation
The concept of orthogonality in mathematics refers to the idea that certain functions can be perpendicular to each other, which means they do not overlap in terms of their value. In this case, we are considering sine functions defined over intervals. The integral given shows that the integral of the product of two sine functions, with different frequencies (m and n), over the same interval is zero. This means that these two functions are orthogonal to each other when m is not equal to n. If m equals n, the integral results in a non-zero value, specifically (a/2). This property is fundamental in Fourier series because it allows us to treat each sine function as an independent basis function that can be used to represent complex functions without interference from each other.
Examples & Analogies
Imagine you are at a concert where several unique instruments (like a violin and a trumpet) are playing different melodies. If you listen closely, you can hear each instrument clearly; they do not drown each other out (like orthogonal functions). However, if two instruments were to play the same note at the same time (like overlapping sine functions), the sound would be much louder—and it wouldn’t be as clear where one sound ends and the other begins. This independence (or orthogonality) is what makes the individual sine functions useful for constructing larger, more complicated sounds (or functions) without overlap.
Integration Over y
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
A similar identity holds for integration over y:
Z b (mπy)(nπy) {0, m≠n
dy = b
b, m=n
0 2
Detailed Explanation
This statement parallels the previous chunk regarding the x-axis. It shows that the sine functions defined in the y-direction also maintain the same orthogonality principle. Integrating the product of two sine functions with different indices over the interval for y results in zero. When the indices are equal, the result is again non-zero, indicating that functions are independent and thus usable for decomposing functions in two dimensions. This reinforces the foundation of Fourier analysis in which functions are expressed as sums of orthogonal components.
Examples & Analogies
Consider a two-dimensional surface, like a chessboard, where each square represents combinations of x and y. Each sine function represents a different ‘move’ on this chessboard. Just like you can move in one direction without interfering with moves in another (a rook's move vertically does not affect a knight's move), the sine functions enable us to analyze different vibration modes independently without mixing the effects.
Importance for Fourier Coefficients
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
These orthogonality properties ensure that each term in the double Fourier series is independent and allow for exact extraction of Fourier coefficients A and B.
Detailed Explanation
The orthogonality of sine functions is not just a mathematical curiosity; it plays a practical role in the extraction of Fourier coefficients, which define how much of each sine wave (or mode) contributes to the overall function represented in the series. This independence of terms means we can calculate each coefficient accurately by integrating with respect to the appropriate sine function. It allows us to focus on one frequency component at a time, ensuring that no overlapping contributions distort our calculation.
Examples & Analogies
Think of a chef preparing a gourmet dish. Each ingredient (like spices, vegetables, and meats) contributes uniquely to the flavor of the dish. If the chef adds too much of one ingredient, it can dominate the other flavors, leading to a poorly balanced meal. In the same way, orthogonality ensures that when we calculate the contributions of each sine function, they do not interfere with one another, resulting in a well-balanced approximation of the original function.
Key Concepts
-
Orthogonality: The condition under which two sine functions are independent over a specified interval.
-
Sine Functions: Trigonometric functions essential for modeling periodic phenomena.
-
Fourier Coefficients: Parameters in the Fourier series that quantify the amplitude of each harmonic.
Examples & Applications
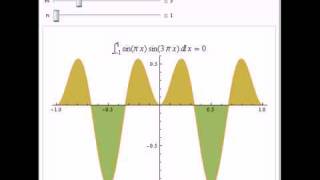
Integrating sin(2πx) and sin(3πx) over the interval [0,1] yields zero, showing their orthogonality.
The integral of sin(2πx) with itself over the same interval yields 1/2, demonstrating its normalized behavior.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Sines that differ, have no overlap, their product is nil, a mathy clap.
Stories
Once on a playground, two sine waves played. When their paths crossed, they never stayed. For whenever one climbed, the other would dip, their integration showed, no overlap in their trip.
Memory Tools
OFT (Orthogonality, Fourier, Terms) - Remember these key phrases when solving for terms in Fourier series.
Acronyms
P.O.W.E.R (Perpendicular, Orthogonal, Wave, Energy, Result) - Use this acronym to recall the significance of orthogonality.
Flash Cards
Glossary
- Orthogonality
The property of functions where their inner product is zero, indicating independence in terms of function space.
- Fourier Coefficients
Constants that are calculated to determine the specific contribution of each mode in a Fourier series expansion.
- Sine Functions
Periodic functions that represent the sine of an angle, critical in defining oscillatory motion.
Reference links
Supplementary resources to enhance your learning experience.
