Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Forced Vibrations
Unlock Audio Lesson
Today, we will discuss forced vibrations, which occur when external, periodic forces act upon a membrane. Does anyone know what this means?
I think it means the membrane vibrates because something is pushing on it, right?
Exactly! Forced vibrations occur due to external influences. For example, if a fan oscillates nearby, it can create forces that impact the membrane's motion.
So, are all vibrations forced then?
Good question! Not all vibrations are forced; some are natural or free vibrations, occurring without external forces. Forced vibrations are just one type.
Remember, the acronym 'FIND' can help us remember: 'F' for Frequency of external forces, 'I' for Influence on amplitude, 'N' for Natural versus forced vibrations, and 'D' for Damping effects.
What's damping?
Great segue! Damping reduces vibration amplitude over time due to energy losses, such as internal friction or air resistance. We will cover that next.
So, to recap on forced vibrations: they arise from external forces affecting membranes. If external forces stop, we revert to free vibrations.
Understanding Damping
Unlock Audio Lesson
Now, let’s delve into damping. Damping plays a significant role in how vibrations decay over time. Can anyone give examples of what might cause damping?
Like when a car's suspension absorbs bumps?
Exactly! Damping mechanisms include internal friction within materials and air resistance. Each contributes to reducing the motion's intensity.
Is there an equation for damping effects?
Yes! We can express damping in the modified wave equation where we include a damping coefficient 'h'. Let’s look at its impact in real-world scenarios.
But how do we actually calculate it?
We often use numerical methods to approximate solutions which help us understand how damping summarizes our systems. Remember this: 'DAMP' can help identify characteristics: 'D' for Damping coefficient, 'A' for Amplitude reduction, 'M' for Methods to analyze, and 'P' for Practical applications in engineering.
So damping is essential for stable structures?
Absolutely! Damping ensures structures can withstand dynamic forces without resonating uncontrollably, improving safety.
Applications in Engineering
Unlock Audio Lesson
Let's relate these concepts to some engineering applications. How might forced vibrations and damping matter in real structures?
Maybe in buildings during earthquakes?
Right on! Engineers design structures to make sure they can handle forces without suffering excessive vibrations, especially during high-stress situations like earthquakes.
What tools can engineers use to analyze these phenomena?
Great question! Engineers can utilize mathematical techniques such as Fourier series, Laplace transforms, and numerical simulations like finite element analysis.
Can we visualize these concepts?
Absolutely! By modeling vibrations and damping using software, we can simulate different conditions and assess how a design will perform. Always think of the acronym 'SIMP' for simulation: 'S' for Simulation tools, 'I' for Impact analysis, 'M' for Modeling vibrations, and 'P' for Practical applications in designs.
So, we use these methods to predict and improve structural integrity?
Precisely! Engineers consistently strategize around vibrations and damping to ensure public safety in various structures.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explores how real-world membranes are affected by external periodic forces (forced vibrations) and how damping, caused by internal friction or air resistance, reduces the amplitude of these vibrations over time. It introduces the modified wave equation that incorporates these factors and hints at various mathematical approaches to analyze them.
Detailed
Forced Vibrations and Damping Overview
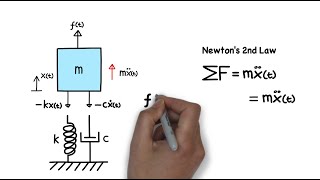
In this section, we examine the realities of vibrating membranes that, unlike theoretical models, experience forced vibrations from external periodic forces and damping from internal friction or air resistance. The behavior of such membranes can be captured mathematically through an extended version of the wave equation:
$$
\frac{\partial^2u}{\partial t^2} + 2h \frac{\partial u}{\partial t} = c^2 \left( \frac{\partial^2u}{\partial x^2} + \frac{\partial^2u}{\partial y^2} \right) + F(x,y,t)
$$
Where:
- $h$ is the damping coefficient,
- $F(x,y,t)$ represents the distribution of the external force acting on the membrane.
Understanding forced vibrations and damping is crucial for engineers as these factors affect the performance and safety of structural elements under dynamic loads. Various mathematical techniques, including Fourier series, Laplace transforms, and numerical methods like finite difference and finite element analysis, can be utilized to analyze these complex equations effectively—becoming increasingly important in civil engineering simulations.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Forced Vibrations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
While the basic model assumes free vibration (i.e., no external force or energy loss), real-world membranes often experience:
• Forced vibration: where external periodic forces act on the system.
Detailed Explanation
In a free vibration system, the object vibrates without any external influence, meaning it moves only because of initial disturbances. However, in real-life scenarios, like a membrane (think of a drum surface), it is often subjected to external forces, known as 'forced vibrations.' These forces can be periodic, meaning they repeat in a cycle, similar to how a drummer strikes a drum repeatedly, causing the membrane to vibrate in response.
Examples & Analogies
Imagine a child on a swing. If they simply swing back and forth without any pushes, that’s free vibration. But if someone pushes them at intervals, now they are experiencing forced vibration. The swing's movement becomes influenced by the pushes, just as a membrane's vibration is influenced by external forces.
Understanding Damping
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Damping: due to internal friction or air resistance, reducing amplitude over time.
Detailed Explanation
Damping refers to the process that reduces the amplitude of vibrations over time. This reduction happens because of energy loss in the system, which can occur due to internal friction within the material or due to air resistance when the object is moving through the air. Think of it as a car's brakes slowing it down; just like brakes dissipate energy and bring the car to a stop, damping removes energy from the vibrating system.
Examples & Analogies
Consider a pendulum. Initially, it swings back and forth vigorously, but over time, its swings become smaller and smaller. This is damping in action. In a physical context, if you’ve ever used a swing at a park and noticed it gradually slows down until it stops, that’s because of damping, where air and friction are stealing energy from the swing.
The Forced Vibration Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For a forced system:
∂²u/∂t² + 2h ∂u/∂t = c²(∂²u/∂x² + ∂²u/∂y²) + F(x,y,t)
where:
• h is the damping coefficient,
• F(x,y,t) is the external force distribution.
Detailed Explanation
This equation describes how a forced system behaves. Each term in the equation represents a different aspect of the system:
- The term ∂²u/∂t² represents the acceleration of the vibration over time.
- The term 2h ∂u/∂t incorporates the effect of damping (h is the damping coefficient). When the system vibrates, it loses energy due to damping, leading to reduced acceleration.
- The terms ∂²u/∂x² and ∂²u/∂y² indicate how the displacement varies across the dimensions of the membrane.
- Finally, F(x,y,t) represents any external forces acting on the system, which could include things like someone pushing down on the membrane.
Examples & Analogies
Think of a trampoline. When you jump on it (the external force F), it starts to vibrate (the displacement). If you keep jumping but the trampoline material is soft and has some give (that's the damping h at play), the trampoline will eventually settle down after you stop jumping because of the energy lost through the material.
Advanced Methods for Engineering Solutions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Though more complex, such equations can also be approached using Fourier series, Laplace transforms, or numerical methods like finite difference or finite element analysis — all vital in advanced civil engineering simulations.
Detailed Explanation
To solve the forced vibration equations, engineers can use several mathematical tools. Fourier series break down complex waveforms into simpler sine and cosine patterns, making analysis easier. Laplace transforms change the equations into a format that is simpler to manipulate mathematically, which can lead to quicker solutions. Numerical methods, like finite difference or finite element analysis, allow for computer simulations of structures, providing insights into how they would behave under various conditions.
Examples & Analogies
Imagine you're trying to understand how waves move on a beach. Instead of studying each wave independently, you can break them down into individual ripples – that's like using Fourier series. If you want to predict how tides will affect your beach over time (like a Laplace transform), you might create a computer model that simulates the waves and tides – akin to using numerical methods, which is what engineers do with complex structures.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Forced Vibrations: Caused by external periodic forces acting on a system.
-
Damping: The reduction in the amplitude of vibrations due to energy dissipation.
-
Wave Equation Modification: Incorporates both damping and external forces for practical analysis.
-
Engineers' Approach: Use of Fourier series and numerical methods to analyze complex vibrations.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Analyzing vibrations in bridge decks subjected to wind forces.
-
Studying the damping behaviors of materials in high-rise buildings during seismic activities.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When forces push or pull, vibrations rule; add damping's touch, and the amplitude shrinks in full.
📖 Fascinating Stories
-
Imagine a bridge that shakes, not by itself but by trucks that pass. But it settles down thanks to its springs that damp the vibrations, keeping it safe.
🧠 Other Memory Gems
-
Remember 'DAMP' for Damping: 'D' is for Damping coefficient, 'A' for Amplitude reduction, 'M' for Methods to analyze, and 'P' for Practical applications.
🎯 Super Acronyms
Use 'FIND' to remember forced vibrations
- 'F' for Frequency of forces
- 'I' for Influence on amplitude
- 'N' for Natural vs. forced
- 'D' for Damping effects.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Forced Vibration
Definition:
Vibrations occurring due to external periodic forces acting on a system.
-
Term: Damping
Definition:
The reduction of vibration amplitude due to energy losses such as internal friction or air resistance.
-
Term: Wave Equation
Definition:
A mathematical equation describing how waves propagate through a medium.
-
Term: Damping Coefficient (h)
Definition:
A parameter that quantifies the amount of damping in a vibrating system.
-
Term: External Force (F)
Definition:
A force applied to a system from outside sources, influencing its motion.