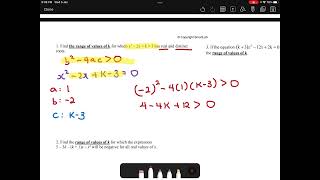
Case 1: Distinct Real Roots (D =b²−4ac>0)
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Distinct Real Roots
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will look into second-order homogeneous equations with distinct real roots. Remember, this is when the discriminant D, calculated as b² − 4ac, is greater than zero.

What does it mean when the roots are distinct and real?

Great question! Distinct roots mean that the quadratic equation yields two different real solutions. This influences the form of our general solution.

So that's why we have two exponentials in the solution?

Exactly! The general solution will be in the form y(x) = C₁e^{r₁x} + C₂e^{r₂x}.
Finding the Characteristic Equation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

To solve a differential equation, we first derive the characteristic equation. What do you think this equation looks like?

Isn't it of the form ar² + br + c = 0?

Exactly right! By solving this quadratic equation, we can determine the roots that will help us construct the general solution.

And how do we know if the roots are distinct?

We check the discriminant. If D = b² − 4ac is greater than zero, we have distinct real roots.
Solving Examples
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s solve an example together. Consider y'' - 5y' + 6y = 0. What’s the first step?

We need to write the characteristic equation, which is r² - 5r + 6 = 0.

Correct! What do we find when we solve this?

The roots r₁ = 2 and r₂ = 3!

Right again! That leads us to the general solution. Can someone write it down?

It would be y(x) = C₁e^{2x} + C₂e^{3x}.

Great job! We can now use initial conditions to solve for the arbitrary constants.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we explore the distinct real roots case of second-order homogeneous linear differential equations, defined by D = b² − 4ac > 0. The general solution is detailed with an example, emphasizing how arbitrary constants are determined by initial conditions.
Detailed
Distinct Real Roots in Second-Order Differential Equations
In this section, we analyze second-order homogeneous linear differential equations characterized by distinct real roots, based on the discriminant condition D = b² − 4ac > 0. When the roots r₁ and r₂ are distinct and real, the general solution of the differential equation can be expressed as:
y(x) = C₁e^{r₁x} + C₂e^{r₂x}
where C₁ and C₂ are arbitrary constants determined by specific initial or boundary conditions related to the problem at hand.
Example
Consider the equation:
y'' - 5y' + 6y = 0
By forming the characteristic equation:
r² - 5r + 6 = 0
we find the roots r₁ = 2 and r₂ = 3. Thus, the general solution becomes:
y(x) = C₁e^{2x} + C₂e^{3x}
This section strongly emphasizes the importance of recognizing root types in determining the behavior of solutions to differential equations, particularly in engineering disciplines.
Youtube Videos









Audio Book
Dive deep into the subject with an immersive audiobook experience.
Conditions for Distinct Real Roots
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Let the roots be r₁ and r₂, with r₁ ≠ r₂ and both real.
Detailed Explanation
In this section, we examine a specific case of second-order differential equations where the discriminant (D), calculated as b²−4ac, is greater than zero. This condition indicates that there are two distinct real roots, r₁ and r₂. The fact that these roots are distinct means that the solutions to the equation will not overlap, leading to unique behavior represented by each root.
Examples & Analogies
Think of looking for two different streets in a city. If both streets exist (distinct real roots), you can take different paths to your destination. If the streets were the same, you'd have no choice. In the same way, distinct real roots give us flexibility in solutions to our differential equation.
General Solution Form
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
General Solution: y(x) = C₁ e^(r₁x) + C₂ e^(r₂x) where C₁ and C₂ are arbitrary constants determined by initial or boundary conditions.
Detailed Explanation
With the identification of distinct real roots, we formulate the general solution of the differential equation. The solution takes the form of a linear combination of exponentials, where each term corresponds to one of the roots. The constants C₁ and C₂ allow us to adjust the solution based on specific initial or boundary conditions relevant to the problem we are modeling.
Examples & Analogies
Imagine you are mixing two different colors of paint to achieve a particular shade. The C₁ and C₂ constants are like the proportions of each color you use. By varying these proportions, you can create a unique color (or solution) that fits the situation at hand.
Example of Distinct Real Roots
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Example: y'' - 5y' + 6y = 0 ⇒ r² - 5r + 6 = 0 ⇒ r = 2, 3 ⇒ y(x) = C₁ e^(2x) + C₂ e^(3x)
Detailed Explanation
Let's illustrate this case with a specific example. The given differential equation, y'' - 5y' + 6y = 0, can be transformed into its characteristic equation r² - 5r + 6 = 0. Solving this quadratic gives us the roots r₁ = 2 and r₂ = 3, confirming they are distinct and real. The general solution of the differential equation then becomes y(x) = C₁ e^(2x) + C₂ e^(3x), where C₁ and C₂ are constants determined by conditions of the problem.
Examples & Analogies
Consider a scenario in which two different tennis balls are dropped from a height. Their distinct behaviors as they fall to the ground represent the two different exponential terms in the solution. Each ball (or term) has its own path but they combine to give the overall motion of the system.
Key Concepts
-
Distinct Real Roots: Occur when the discriminant D > 0, yielding two different real solutions.
-
Characteristic Equation: The polynomial equation derived from a differential equation to find its roots.
-
General Solution: Formed based on the nature of the roots, represented using exponential functions.
Examples & Applications
Solving the equation y'' - 5y' + 6y = 0 gives us distinct real roots, resulting in the solution y(x) = C₁e^{2x} + C₂e^{3x}.
Given initial conditions y(0) = 3 and y'(0) = 5, we can determine specific values for C₁ and C₂.
Memory Aids
Interactive tools to help you remember key concepts
Memory Tools
Remember D for Distinct: D > 0 means distinct roots show a sparkle in growth!
Acronyms
D.R.E.A.M. - Distinct Real Example
Acknowledges roots are different and real.
Rhymes
Roots can be distinct, they help us link, giving solutions that never sink.
Stories
Once upon a time, two roots named r1 and r2 lived in a quadratic village. They were distinct and different from each other, bringing unique solutions to the equations they lived in.
Flash Cards
Glossary
- Distinct Real Roots
Roots of the characteristic equation that are different real numbers, occurring when D = b² − 4ac > 0.
- Characteristic Equation
A quadratic equation derived from a second-order differential equation used to find its roots.
- General Solution
The complete solution of a differential equation involving arbitrary constants determined by initial conditions.
- Discriminant
A calculation (D = b² − 4ac) that reveals the nature of the roots of a quadratic equation.
Reference links
Supplementary resources to enhance your learning experience.
