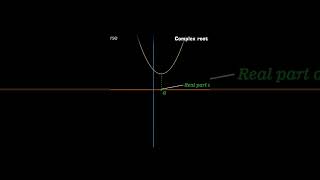
3.3.3. Case 3: Complex Roots (D <0)

Let the roots be complex: r = α ± iβ

In the context of second-order homogeneous differential equations, complex roots occur when the discriminant (D) is less than zero (D < 0). This signifies that the equation does not yield distinct real roots, which changes the nature of the solutions significantly. Instead of yielding straightforward exponential functions, complex roots introduce oscillatory behavior into the solutions.

Imagine a swing (oscillator) that moves back and forth. When the swing is pushed gently, it moves in regular oscillations. Complex roots in differential equations can be thought of as describing how things like vibrations work in engineering, where instead of moving in a straight line, structures might sway back and forth.

General Solution: y(x) = e^αx (C cos(βx) + C sin(βx))

The solution format for equations with complex roots incorporates both exponential and trigonometric functions. The term 'e^αx' represents an exponential function that dictates the growth or decay of the overall solution, while the terms 'C cos(βx)' and 'C sin(βx)' represent oscillations. This reflects that under certain conditions, structures will not just react instantaneously but will also show oscillatory motion over time.

Consider a building during an earthquake. The building doesn’t just sway left and right; it has a natural frequency at which it oscillates. The general solution captures both the gradual change in the amplitude (from the exponential part) and the oscillatory nature (from the sine and cosine parts), much like how the building would sway as the forces fluctuate.

This represents damped oscillations—highly relevant in civil engineering (e.g., vibration analysis, seismic behavior).

Damped oscillations refer to the situation where the amplitude of oscillation decreases over time due to an external force, such as friction or resistance from the environment. In civil engineering, understanding damped oscillations is crucial when designing structures that can withstand vibrations from earthquakes or wind, as it affects the stability and safety of buildings.

Think of how a swing gradually comes to rest over time when air resistance slows it down. In engineering, if a building sways during an earthquake, dampers are often installed to reduce the swing amplitude over time, ensuring that the structure remains stable. The principles of damped oscillation help engineers create resilient designs.

Example: y′′ + 2y′ + 5y = 0 ⇒ r² + 2r + 5 = 0 ⇒ r = −1 ± 2i ⇒ y(x) = e^(−x)(C cos(2x) + C sin(2x))

This example shows how to connect the characteristic equation to the general solution for complex roots. The roots are calculated from the characteristic equation, which gives us r = −1 ± 2i. The negative real part (−1) implies decay in amplitude, while the imaginary part (±2i) introduces oscillation. Thus, our final general solution clearly reflects these attributes.

This is similar to tuning a musical instrument. If the tension is too tight or loose (analogous to the real part of the roots), the pitch changes, while oscillating produces the sound waves or vibrations we hear (related to the imaginary part). The overall sound diminishes over time, showing how different elements interact just like in structural dynamics.

--