Engineering Insight: Damping in Vibrations
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Damping Ratio
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're diving into the significance of damping in structural dynamics. Let's start by discussing the damping ratio. Who can explain what the damping ratio is?

Isn't it related to how much a system dampens out vibrations over time?

Exactly! The damping ratio is defined as ζ = c / (2√(km)), where 'c' is the damping coefficient, 'm' is mass, and 'k' is stiffness. It's essential for understanding the behavior of vibrating systems.

So how does this ratio categorize the system's behavior?

Great question! If ζ > 1, the system is overdamped. If ζ = 1, it's critically damped, and if ζ < 1, it’s underdamped. Remember this acronym: O, C, U for Overdamped, Critically damped, Underdamped.

What does each case mean in practical terms?

Overdamped means the system returns to equilibrium slowly, critically damped systems return as quickly as possible without oscillating, and underdamped systems oscillate before settling down. Understanding these behaviors helps engineers design better structures.
Applications in Civil Engineering
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's discuss how these concepts apply in civil engineering. Why is damping important for structures like buildings and bridges?

It probably helps them resist forces from things like wind and earthquakes.

Exactly! By ensuring that structures are designed with the appropriate damping ratio, engineers can mitigate the effects of seismic activity, ensuring safety and stability.

So, when designing a building, how do engineers decide on the right damping system?

Good question, Student_1! They analyze factors like material properties, expected seismic loads, and the intended use of the structure to optimize damping characteristics.

That sounds complex but crucial for safety!

It is! Remember, when we design structures, we want to control their response to dynamic forces. Calm and steady wins the structural race!
Exploring Overdamped, Critically Damped, and Underdamped Vibration Responses
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's explore what happens in each type of damping. Student_3, can you describe what happens in an overdamped system?

In an overdamped system, the response is slow and doesn't oscillate, right?

Correct! Now, Student_2, can you explain critically damped systems?

They return to equilibrium quickly without oscillating. It seems like the ideal situation.

Spot on! Lastly, Student_4, what about underdamped systems?

Those systems oscillate and take time to settle down but are more dynamic.

Exactly! Understanding these responses helps engineers design safer structures under dynamic loads. Remember the mnemonic: Overdamped is 'slow and steady,' critically damped is 'quick and calm,' and underdamped is 'dance before rest.'
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
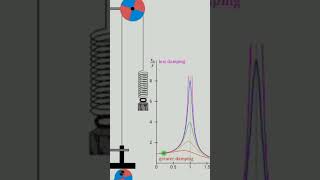
Damping is a crucial aspect of vibrations in civil engineering, characterized by the damping ratio, which influences whether the system is overdamped, critically damped, or underdamped. A proper understanding of these concepts helps engineers design structures resilient to seismic activities.
Detailed
In structural dynamics, the behavior of a damped vibrating system is modeled by the differential equation d²x/dt² + c(dx/dt) + kx = 0, where 'm' is the mass, 'c' is the damping coefficient, and 'k' is the stiffness. The damping ratio ζ = c / (2√(km)) categorizes the system's oscillatory behavior:
- If ζ > 1: The system is overdamped, exhibiting real distinct roots.
- If ζ = 1: The system is critically damped, showing repeated roots.
- If ζ < 1: The system is underdamped, leading to complex roots that reflect oscillatory motion.
Civil engineers rely on these damping characteristics while designing buildings and bridges to ensure they can withstand seismic activity, maintaining structural integrity and safety.
Youtube Videos



![Damped Free Vibrations with Viscous Damping-Theory (Equation of motion) [DOM]](https://img.youtube.com/vi/YpiSZxDj7ws/mqdefault.jpg)





Audio Book
Dive deep into the subject with an immersive audiobook experience.
The Damped Vibrating System Equation
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In structural dynamics, the equation:
d2x dx
m +c +kx=0
dt2 dt
models a damped vibrating system.
Detailed Explanation
This equation represents a damped vibrating system, where:
- m is the mass of the system, which is crucial because it affects how much force is needed to move it.
- c is the damping coefficient, which measures how much energy is lost due to damping forces, such as friction or air resistance.
- k is the stiffness of the system, indicating how resistant it is to deformation.
Together, these components determine how the system behaves when it is set into motion, especially how it returns to equilibrium after being disturbed.
Examples & Analogies
Imagine a swing at a playground. When you push the swing (applying force), the heavy swing (mass) starts moving but gradually slows down due to air resistance (damping). The swing doesn’t just stop immediately; it oscillates back and forth before settling down, which mirrors how the equation governs real-world systems.
Understanding the Damping Ratio
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Define damping ratio:
ζ = c / (√(k * m)), ω = √(k / m)
Then the system’s behavior is:
• ζ >1: Overdamped (real distinct roots)
• ζ =1: Critically damped (repeated roots)
• ζ <1: Underdamped (complex roots)
Detailed Explanation
The damping ratio (ζ) is a key parameter that helps classify the behavior of the damped system:
- Overdamped (ζ > 1): The system returns to equilibrium without oscillating, moving slowly.
- Critically damped (ζ = 1): This scenario allows the system to return to equilibrium as quickly as possible without oscillating.
- Underdamped (ζ < 1): The system oscillates while gradually coming to rest, which can be seen in many real-life applications like car suspensions.
Understanding these behaviors is crucial for designing systems that respond appropriately to external forces.
Examples & Analogies
Consider the shock absorbers in a car. If they are too soft (underdamped), the car bounces too much after going over a bump. If they are too stiff (overdamped), the car feels like it takes too long to settle after the bump. The ideal scenario (critically damped) is where the car smoothly returns to a stable position without excessive bouncing or delay.
Application in Civil Engineering
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Application: Civil engineers design buildings and bridges to respond within a controlled damping range to seismic activity.
Detailed Explanation
Engineers use the concepts of damping ratios to design structures that can respond effectively to seismic activity (earthquakes). By ensuring that the damping is sufficient, they can prevent buildings from swaying excessively and collapsing during an earthquake. The goal is to design structures that can dissipate the energy from seismic waves through controlled oscillations, keeping both safety and comfort in mind.
Examples & Analogies
Think of a tall skyscraper during an earthquake. If it's built using appropriate damping techniques (like special materials or dampers), it may sway gently back and forth but will not topple over. This is similar to how a well-tuned guitar string vibrates but does not break under pressure. Good damping designs in civil engineering ensure that buildings stand tall and safe, even in a tremor.
Key Concepts
-
Damping Ratio (ζ): A critical parameter defining how a vibrating system responds to oscillations.
-
Types of Damping: Overdamped, critically damped, and underdamped systems each behave distinctly under dynamic conditions.
-
Practical Application: Engineers use damping characteristics to improve the safety and resilience of structures.
Examples & Applications
A building designed with a damping ratio less than one will oscillate during an earthquake but will return to rest after the shaking.
A bridge that is critically damped will quickly stabilize after being disturbed by strong winds.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
If ζ is high, the oscillations die, but too low makes them fly!
Acronyms
O.C.U
Overdamped
Critically damped
Underdamped.
Stories
Imagine a swing at a park - too much friction keeps it still (overdamped), just enough allows it to swing without stopping (critically damped), and just a little lets it go wild (underdamped).
Memory Tools
Remember: Overdamped = slow & steady, Critically damped = quick but calm, Underdamped = dance before rest.
Flash Cards
Glossary
- Damping Ratio (ζ)
A dimensionless measure of damping within a system, which characterizes the system's oscillatory behavior.
- Overdamped System
A system where the damping is so high that it returns to equilibrium without oscillating.
- Critically Damped System
A system that returns to equilibrium as quickly as possible without oscillating.
- Underdamped System
A system that oscillates before settling to equilibrium.
- Dynamic Loads
Forces acting on a structure that vary with time, such as wind or earthquakes.
Reference links
Supplementary resources to enhance your learning experience.
