Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Statically Determinate Trusses
Unlock Audio Lesson
Let's start our discussion by defining what a statically determinate truss is. Can anyone tell me how we determine this?
Is it when we can find all the forces using just the equations of statics?
Exactly! We can solve for the internal forces using equilibrium equations alone. Can someone remind us of the main equations we use?
There are equations for summing forces in the X and Y directions and a moment equation too!
Right! Then can someone explain what happens if we can't solve for the forces in this way?
The truss would be considered statically indeterminate?
Correct! This leads us to the importance of knowing how to calculate the reactions. Let's explore external determinacy next.
External vs. Internal Determinacy
Unlock Audio Lesson
Now, let's talk about external and internal determinacy. External determinacy focuses on reactions at supports. Can anyone share the conditions for this?
A truss is externally determinate if the number of reactions is three or fewer for 2D or six or fewer for 3D?
Exactly! And what about internal determinacy? How do we determine that?
It depends on the relationship between the number of members, reactions, and joints, right? Like m + R = 2j for 2D?
Perfect! So, what can we deduce if m + R exceeds 2j or 3j?
Then it’s statically indeterminate, but if it's less than that, the truss is unstable?
Yes! Now let's summarize these key points.
Condition of Stability
Unlock Audio Lesson
Moving on, let’s discuss the stability of trusses! When do we say that a truss is not stable?
When the number of members is less than twice the number of joints for 2D, right?
Yes, if m < 2j, the truss is considered unstable. Can anyone explain why a truss needs to be stable?
Because an unstable truss wouldn't maintain its shape when loads are applied?
Exactly! Stability is essential for functionality. Let’s recap stability and determinacy together.
Application of Concepts
Unlock Audio Lesson
Alright, let’s apply what we’ve learned. Imagine a truss where m = 6 and j = 5. Can someone determine whether this truss is internally stable?
Since m + R would be 6 + R, and if R is 3 or fewer, it will be less than 2j!
Correct! Now if R = 3, what can we say about the statics of this truss?
It would be unstable, since 12 should be the minimum for stability!
Great job! How can we summarize our findings about stability?
Trusses must have enough members to support their stability, ensuring they can withstand applied loads!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
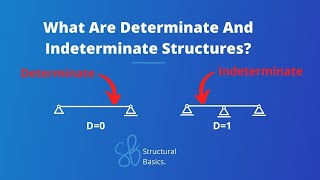
Trusses are categorized as statically determinate if their internal bar forces can be determined solely from static equilibrium equations. The section outlines necessary equations and conditions that dictate the stability and determinacy of trusses, distinguishing between externally and internally determinate structures.
Detailed
Determinacy and Stability of Trusses
In structural engineering, trusses are considered statically determinate if all internal forces can be calculated from the equations of statics alone. If this is not possible, the truss is termed statically indeterminate. There are two categories of determinacy:
- External Determinacy: This is assessed based on the reactions at the supports. A truss is externally determinate if the number of reactions (R) is less than or equal to three in 2D or six in 3D structures.
- Internal Determinacy: This refers to the relationship between the number of joints (j), the number of members (m), and the number of reactions (R). A truss is internally determinate if the number of unknowns (m + R) is equal to twice the number of joints for 2D (or three times for 3D), leading to m + R = 2j (or 3j).
Additionally, a truss that has fewer members than needed for stability (m < 2j for 2D or m < 3j for 3D) is considered unstable, meaning it cannot maintain its shape under load. The section ties these concepts together, providing a fundamental understanding necessary for analyzing trusses.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Statically Determinate Trusses
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Trusses are statically determinate when all the bar forces can be determined from the equations of statics alone. Otherwise, the truss is statically indeterminate.
Detailed Explanation
A statically determinate truss is one where the forces in the bars (members) can be found using just the basic equations of equilibrium. These equations are derived from Newton's laws, and they state that a system in static equilibrium must have all forces balanced and no net moments. If a truss cannot be analyzed this way, it’s classified as statically indeterminate, meaning that additional methods are needed to determine the forces in the members.
Examples & Analogies
Imagine trying to find the forces acting on a group of three people holding a heavy beam. If enough information is provided about how they are positioned and the beam's weight, you can calculate how much force each person needs to exert simply using basic physics. This setup is 'statically determinate'. However, if their positions or connections add complexity and hinder clear calculations, you would need more detailed analysis, which is similar to dealing with a statically indeterminate truss.
External Determinacy
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A truss may be statically/externally determinate or indeterminate with respect to the reactions (more than 3 or 6 reactions in 2D or 3D problems respectively).
Detailed Explanation
In a structural context, external determinacy refers to the ability to ascertain the support reactions of a truss using statics alone. In two-dimensional analysis, a truss can be external determinate if it has three or fewer external reactions. In three-dimensional cases, that number increases to six. If it has more reactions than these limits, the truss is considered externally indeterminate.
Examples & Analogies
Consider a see-saw on two supports. If you were to add a third support point, it may introduce redundancy in how the weight is supported, complicating how you may analyze the forces acting on the see-saw. Similarly, if a truss has too many supports, it can make finding the forces at those points more complex and indeterminate.
Internal Determinacy
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A truss may be internally determinate or indeterminate. If we refer to j as the number of joints, R the number of reactions, and m the number of members, then we would have a total of m+R unknowns and 2j (or 3j) equations of statics (2D or 3D at each joint).
Detailed Explanation
Internally, a truss is determined by its connectivity and member arrangement. Internal determinacy involves ensuring sufficient equations to solve for member forces. In a 2D truss, the relationship between the number of members (m), reactions (R), and joints (j) is essential: if the total unknowns (m + R) exceed the available equations (2j), then it is internally indeterminate. Conversely, if there are fewer unknowns than equations, the structure may be unstable.
Examples & Analogies
Think of a family where each member must share chores. If there are more chores than members who can do them, they might need to cooperate to determine who does what—similar to a determinate system. If there are more members than chores, there could be confusion about who does what, leading to instability—akin to an indeterminate system.
Conditions for Stability
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
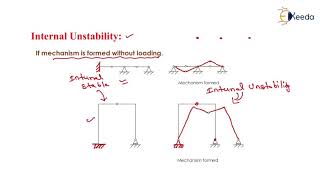
If m < 2j (in 2D), the truss is not internally stable, and it will not remain a rigid body when it is detached from its supports.
Detailed Explanation
For a 2D truss to be internally stable, there must be enough members to ensure that it can maintain its shape without external stiffness. Specifically, if the number of members (m) is less than twice the number of joints (2j), the truss will not hold its shape when the support is removed, indicating that it’s not rigid. This underscores the importance of member arrangement in structural designs.
Examples & Analogies
Imagine a spider web; if there aren't enough lines connecting the points, the web collapses when a few points are removed (like supports being taken away). A well-constructed web (truss) needs enough connections to stay upright and not fall apart.
Equations of Equilibrium
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Since each joint is pin-connected, we can apply (ΣM = 0) at each one of them. Furthermore, the summation of forces applied on a joint must be equal to zero.
Detailed Explanation
Each joint in a truss operates under the principle of equilibrium. At every pin-connected joint, the sum of the forces acting on it must equal zero, which reflects that the joint isn't moving (is in static equilibrium). This principle can be expressed using equilibrium equations such as ΣF_x = 0, ΣF_y = 0, and in 3D, the sum of moments ΣM also equals zero to ensure stability and balance.
Examples & Analogies
Picture a playground swing. If a child is sitting perfectly still, the forces from the swing's connection to the frame and their weight balance each other out. Just as the swing rests motionlessly, a truss joint balances forces to maintain structural integrity.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Static Determinacy: A truss is statically determinate if all forces can be calculated using equilibrium equations.
-
External Determinacy: Relates to support reactions; a truss is considered externally determinate if R ≤ 3 in 2D or R ≤ 6 in 3D.
-
Internal Determinacy: A condition where m + R must equal 2j for 2D (or 3j for 3D) for the truss to be stable.
-
Stability: A truss is stable when it can resist loads without deforming; requires the right number of members.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: A simple triangular truss with 3 members and 3 joints is statically determinate because it satisfies the condition m + R = 2j.
-
Example 2: A square truss with 4 members and 8 joints is statically indeterminate if we consider more reactions than necessary.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
For a truss to be stable and fair, members must be plenty, so shapes won't tear.
📖 Fascinating Stories
-
Imagine a builder using too few beams for a bridge. When the winds blew, one side collapsed—showing the importance of stability.
🧠 Other Memory Gems
-
RJS (Reactions Just Survive): Remember Relations of Members, Joints, and Stability.
🎯 Super Acronyms
DEB (Determine Equilibrium Balance)
- Helps to recall how to check truss equilibria.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Statically Determinate Truss
Definition:
A truss in which all internal forces can be calculated solely using the equations of static equilibrium.
-
Term: Statically Indeterminate Truss
Definition:
A truss that cannot be analyzed for internal forces using only static equilibrium equations due to surplus unknowns.
-
Term: External Determinacy
Definition:
Refers to a condition where the truss reactions are within the allowable limits, generally determined by the support conditions.
-
Term: Internal Determinacy
Definition:
A condition ensuring that the truss has enough bars or members to maintain its internal forces appropriately, based on the number of joints and reactions.
-
Term: Equations of Equilibrium
Definition:
Mathematical statements used to analyze static systems, typically summing forces and moments to zero.