Introduction
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Trusses
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we'll be discussing trusses, an essential component in structural engineering. Can anyone tell me what a truss is?

Isn't it a structure made up of connected bars?

Exactly! Trusses are composed of bars that transfer forces. They mainly support axial forces. Would anyone like to explain how trusses differ from cables?

Cables can only handle tensile forces, right? Trusses can handle both tension and compression.

Well done! Remember, this allows trusses to be used in various applications like bridges and roofs. Let's not forget, the structure of a truss often includes triangular elements to maintain its strength.
Assumptions in Truss Analysis
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's delve into the assumptions that we make when analyzing trusses. Can anyone list a few?

I think one is that the bars are pin-connected.

Correct! Pin connections imply that joints act like frictionless hinges. What do you think this means for analyzing the loads?

It means we only apply loads at the joints, right?

Absolutely! This simplification is critical for our calculations. We also use these assumptions to determine internal forces along the members effectively.
Types of Forces in Trusses
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's move on to the types of forces we encounter in trusses. What are they?

Tension and compression, I think.

Exactly! Tensile forces pull the bars apart, while compressive forces push them together. Remember, the placement of diagonal members determines what type of force they experience. Can anyone give me an example?

In a Pratt truss, the diagonals are in tension, correct?

Correct! Understanding these forces helps in the design of more efficient structures. Great job, everyone!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we explore the key aspects of trusses, including the assumptions made in their design, the distinctions between cables and trusses, and the significance of their structure in various applications. We will also evaluate basic relations governing truss analysis.
Detailed
Introduction
In this section, we aim to provide a foundational understanding of trusses—their structure, the types of forces they carry, and key assumptions involved in their design. Trusses are defined as two-dimensional or three-dimensional structures made from simple, linear components that primarily transfer axial forces. Unlike cables, which only support tensile forces, trusses can resist both tensile and compressive forces, making them suitable for a variety of engineering applications.
Key Assumptions:
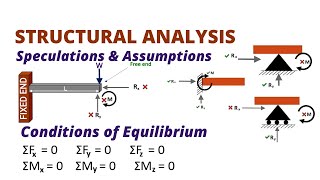
When analyzing trusses, it is essential to consider the following assumptions:
1. Bars are pin-connected.
2. Joints function as frictionless hinges.
3. Loads are applied solely at the joints.
Typically, trusses are composed of triangular elements, with compressive forces acting on the upper chord and tensile forces on the lower chord. The orientation of the diagonal members in the truss determines whether they are subject to tension or compression.
Applications of trusses are vast, ranging from bridges to long-span roofs, electric towers, and even space structures. By understanding the properties and assumptions of trusses, engineers can design more effective structures, making this foundation crucial in structural engineering.
Youtube Videos









Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Cables and Trusses
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Cables and trusses are 2D or 3D structures composed of an assemblage of simple one-dimensional components which transfer only axial forces along their axis. Cables can carry only tensile forces, trusses can carry tensile and compressive forces.
Detailed Explanation
This chunk defines cables and trusses. Cables are flexible structures that can only bear forces that pull on them (tensile forces), while trusses are more rigid and can bear forces that either push or pull (tensile and compressive forces). Axial forces are forces that act along the length of a member, meaning that cables and trusses are designed to react primarily to these types of forces.
Examples & Analogies
Imagine a clothesline (a cable) that only holds your clothes up by pulling on them with tension. Now think of a bicycle frame (a truss), which uses both tension and compression to keep its shape and support a rider.
Properties of Cables and Trusses
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Cables tend to be flexible, and hence, they tend to oscillate and therefore must be stiffened. Trusses are extensively used for bridges, long span roofs, electric towers, and space structures.
Detailed Explanation
Cables are known for their flexibility, which makes them susceptible to swaying or oscillating in the wind; hence, they require additional supports or stiffening methods to maintain stability. On the other hand, trusses are preferred in various construction applications, such as bridges or roofs, due to their strength and ability to span larger distances without sagging.
Examples & Analogies
Think about a suspension bridge where the cables need to withstand the sway caused by strong winds. Engineers take care to design the system so that the cables don't oscillate excessively. The structure of the bridge, made up of trusses, allows it to carry heavy traffic without collapsing.
Assumptions in Truss Design
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
For trusses, it is assumed that
1. Bars are pin-connected
2. Joints are frictionless hinges
3. Loads are applied at the joints only.
Detailed Explanation
Three key assumptions streamline truss analysis: first, that the bars are connected at the joints like pins, allowing rotation, which simplifies force calculations. Second, the joints act as frictionless hinges to allow free movement without resistance. Lastly, loads are considered to act at the joints, rather than along the bars, which simplifies structural analysis.
Examples & Analogies
Imagine a mobile toy where different pieces connect at joints. The ease of movement at the joints represents frictionless connections. If weights (loads) are added to specific joints as you play, those areas are where the toy would need to be most stable, just like in a truss.
Truss Composition
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
A truss would typically be composed of triangular elements with the bars on the upper chord under compression and those along the lower chord under tension.
Detailed Explanation
Trusses are commonly made up of triangular shapes. This design is effective because, in a triangle, the structure is more stable when under different loads. The upper parts of the truss (the upper chord) experience compressive forces, meaning they are being pushed together, while the lower parts (the lower chord) experience tensile forces, meaning they are being pulled apart.
Examples & Analogies
Think of a classic triangle you see in a bridge. If you imagine pushing down on the peak (the top part of a triangle), the base holds it together, just like how the bars of the truss work under the forces acting on them.
Examples of Common Truss Types
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Fig. 4.1 illustrates some of the most common types of trusses. It can be easily determined that in a Pratt truss, the diagonal members are under tension, while in a Howe truss, they are in compression.
Detailed Explanation
The text mentions common types of trusses, such as the Pratt and Howe trusses. Each type has its structural characteristics based on the arrangement of their members. In a Pratt truss, the diagonal members are designed to be tension members, making them suited for materials that resist tension effectively. In contrast, the Howe truss uses diagonal members that experience compression, which can be more favorable for heavier timber constructions.
Examples & Analogies
Consider two types of trees: the tall and slender poplar tree represents the Pratt truss handling wind, while the stout oak represents the Howe truss that can handle heavier loads. Each structure uses its form to maintain stability and strength in the face of pressures.
Key Concepts
-
Trusses: Structures made of linear components that carry axial forces.
-
Pin connections: Allow rotation and do not transfer moments between members.
-
Tension and Compression: The two main forces that trusses resist.
Examples & Applications
A bridge constructed using a Pratt truss design effectively transmits loads through its tension and compression factors, making it suitable for long spans.
Roof structures often utilize trusses to maximize space underneath while providing robust support.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In a truss, bars are tied, tension pulls, compression's pride.
Stories
Imagine a bridge supported by a truss made of strong steel. The upper members feel the push while the lower ones pull, creating a safe way across!
Memory Tools
Remember 'PIN' for truss assumptions: Pin-connected, In joints, No moments.
Acronyms
TAC - Tension, Assumptions, Compression to remember truss roles.
Flash Cards
Glossary
- Tension
An axial force that pulls or stretches a member.
- Compression
An axial force that pushes or shortens a member.
- Pinconnected
A type of joint connection that allows rotation without transfer of moments.
Reference links
Supplementary resources to enhance your learning experience.
