Dijkstra's Algorithm (Shortest Path)
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Dijkstra's Algorithm
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Welcome, everyone! Today we’re diving into Dijkstra's Algorithm, which is used for finding the shortest path in a weighted graph with non-negative edges. Can anyone tell me what we mean by a 'weighted graph'?

Is it a graph that uses weights to represent distances or costs between nodes?

Exactly! The edges in a weighted graph have values that typically represent distances or costs. This is crucial for Dijkstra's since we need to calculate the shortest routes. What do you think would happen if the weights were negative?

Wouldn’t that make the algorithm unreliable or give incorrect results?

Right again! Dijkstra's Algorithm doesn't handle negative weights correctly. So, we'll focus on graphs with non-negative weights. Let's remember this with the acronym 'NICE'—Non-negative, Important for Correct Evaluation.

So, 'NICE' helps us remember the graph weight requirement!

Perfect! Let’s explore how Dijkstra's works step by step.
How Dijkstra's Algorithm Works
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Dijkstra’s Algorithm starts at the source node and works by visiting all its neighboring nodes. Who can tell me how it knows which node to explore next?

Does it pick the node with the smallest distance value?

That’s correct! The algorithm uses a priority queue to always expand the next node that has the smallest known distance from the source. This ensures optimal path finding. Remember, we can think of this concept as 'Priority for Progress'—we prioritize exploration based on distance.

So, after visiting a node, it updates the distances to its adjacent nodes, right?

You got it! If we find a shorter path to one of the neighboring nodes, we update its distance. This process continues until we’ve explored all the nodes. Let’s summarize this with the mnemonic 'TREAD'—Traverse, Relax distances, Explore neighbors, Acknowledge updates, Done when all nodes processed.

That’s a good way to remember the steps!
Applications of Dijkstra's Algorithm
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now that we understand how Dijkstra's Algorithm works, let’s discuss where it is used in the real world. Can anyone give me an example?

I think it’s used in GPS systems for finding the shortest driving route.

Exactly! GPS navigation is a prime application. It calculates the shortest route from point A to point B efficiently using the distances on the roads as weights.

Are there any other applications besides GPS?

Yes, absolutely! Dijkstra's is also used in network routing protocols to determine optimal pathways for data transmission. We can remember this idea with the acronym 'GRASP'—Graph Routing and Shortest Path mechanism.

That’s useful to know, especially in technology!
Time Complexity of Dijkstra's Algorithm
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Finally, let’s look at the time complexity of Dijkstra's Algorithm. When we use a min-heap for the priority queue, what do we get?

Would it be like O((V + E) log V) time complexity?

Correct! That makes it quite efficient for large graphs. We can remember this with 'Efficiently Evaluating Graphs'—E for efficiency, V for vertices, E for edges.

That helps clarify its efficiency!

Great! Now we have a comprehensive understanding of Dijkstra's Algorithm—how it works, where it's used, and how efficient it is. This foundational knowledge is key in any graph theory applications.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
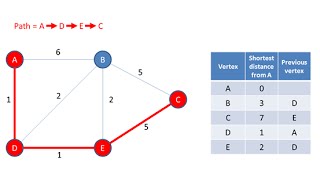
Dijkstra's Algorithm is a cornerstone algorithm in graph theory that calculates the shortest path from a starting node to all other nodes in a graph with weighted edges. Its time complexity can be optimized using a priority queue implemented with a min-heap, allowing for efficient calculation even in large graphs.
Detailed
Detailed Summary of Dijkstra's Algorithm
Dijkstra's Algorithm is utilized to determine the shortest paths from a single source vertex to all other vertices in a graph characterized by non-negative edge weights. This algorithm serves pivotal applications in various fields, including routing and network navigation.
Key Concepts
- Weighted Graphs: Dijkstra’s Algorithm requires a graph where edges can have weights, representing the cost or distance between nodes. Non-negative weights ensure the algorithm's correctness and reliability.
- Implication of Time Complexity: The algorithm's performance is primarily dependent on the number of vertices (V) and edges (E) in the graph. Utilizing a priority queue for edge selection, the time complexity can reach O((V + E) log V), making it suitable for sparse and dense representations alike.
- Application in Real-world Scenarios: Its applications range from GPS navigation systems to network routing, where efficiently determining the shortest path is vital for performance and user experience.
Dijkstra's Algorithm is an essential tool in the arsenal of algorithms for navigating and analyzing complex networks, combining simplicity and efficiency.
Youtube Videos
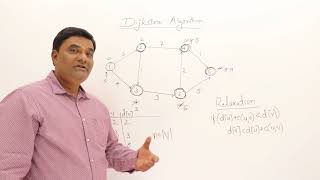






![[7.5] Dijkstra Shortest Path Algorithm in Python](https://img.youtube.com/vi/OrJ004Wid4o/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Purpose of Dijkstra's Algorithm
Chapter 1 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Used in weighted graphs (non-negative edges) to find the shortest path from a source to all vertices.
Detailed Explanation
Dijkstra's Algorithm is a method used to determine the shortest path between nodes in a weighted graph. A weighted graph is one where each edge has a numerical value (weight) associated with it. Typically, these weights represent costs, distances, or times. The algorithm efficiently finds the shortest distance from a designated starting node (the 'source') to all other nodes in the graph, ensuring that it only considers edges with non-negative weights.
Examples & Analogies
Imagine you are planning a road trip and using a map. Each road between locations has a distance labeled on it, representing how far apart those locations are. Dijkstra's Algorithm helps you determine the best route that will minimize your total driving distance, starting from your home to every possible destination in the area.
Time Complexity of Dijkstra's Algorithm
Chapter 2 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Time: O((V + E) log V) with Min-Heap
Detailed Explanation
The algorithm's time complexity of O((V + E) log V) indicates how the algorithm's running time increases with the number of vertices (V) and edges (E) in the graph. Here, 'log V' often arises from utilizing a Min-Heap to efficiently retrieve the next closest vertex from the source node. As new vertices are discovered, they are added to this heap. The computational cost is driven by two factors: exploring each vertex V and evaluating each edge E, combined with the logarithmic cost associated with managing the Min-Heap.
Examples & Analogies
Think of Dijkstra’s Algorithm like a job where someone distributes flyers in a neighborhood. Each house represents a vertex, and the paths between them represent edges with distances. Every time this person decides the next house to go to, they check their map (the Min-Heap) to find the closest house they haven’t visited yet. The process of checking distances and moving to the next location takes time; similarly, the more houses and paths there are, the longer it takes overall to finish distributing.
Key Concepts
-
Weighted Graphs: Dijkstra’s Algorithm requires a graph where edges can have weights, representing the cost or distance between nodes. Non-negative weights ensure the algorithm's correctness and reliability.
-
Implication of Time Complexity: The algorithm's performance is primarily dependent on the number of vertices (V) and edges (E) in the graph. Utilizing a priority queue for edge selection, the time complexity can reach O((V + E) log V), making it suitable for sparse and dense representations alike.
-
Application in Real-world Scenarios: Its applications range from GPS navigation systems to network routing, where efficiently determining the shortest path is vital for performance and user experience.
-
Dijkstra's Algorithm is an essential tool in the arsenal of algorithms for navigating and analyzing complex networks, combining simplicity and efficiency.
Examples & Applications
In GPS navigation, Dijkstra's Algorithm calculates the fastest route from one location to another based on road distances.
In network routing, Dijkstra's Algorithm determines the optimal path for data packets to travel efficiently.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In a weighted graph, oh so keen, Dijkstra finds paths, neat and clean.
Stories
Imagine a courier delivering packages through a city; Dijkstra helps him find the shortest route avoiding unpleasant traffic.
Memory Tools
NICE - Non-negative, Important for Correct Evaluation.
Acronyms
TREAD - Traverse, Relax distances, Explore neighbors, Acknowledge updates, Done when all processed.
Flash Cards
Glossary
- Dijkstra's Algorithm
An algorithm used to find the shortest paths from a source node to all other nodes in a weighted graph with non-negative edges.
- Weighted Graph
A graph in which edges have weights, representing the cost or distance between the vertices they connect.
- Priority Queue
A data structure that allows for the efficient retrieval of the smallest or highest priority element.
- MinHeap
A binary tree where the value of each node is less than or equal to the values of its children, often used to implement priority queues.
- Time Complexity
A computational complexity that estimates the amount of time an algorithm will take to complete based on the input size.
Reference links
Supplementary resources to enhance your learning experience.
