Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Tries
Unlock Audio Lesson
Today we're going to discuss tries, also known as prefix trees. Can anyone tell me what a tree structure might look like?
A tree has nodes, with a root at the top and branches leading to other nodes, right?
Exactly! A trie is a special kind of tree where each node represents a character in a string. What do you think can be some advantages of using this structure?
Maybe it helps in searching for strings faster?
Absolutely! The lookup time in a trie is O(length of the word), making it efficient for applications like autocomplete. Let's remember that with the acronym 'FAST' for 'Find And Search Trie'.
Uses of Tries
Unlock Audio Lesson
Can anyone give examples of where tries might be used in real-life applications?
I think they could be used in search engines, right?
Yes! They're also used in spell checking and autocomplete features in many text editors. Does anyone know why this structure fits those needs so well?
Because they can store and find prefixes quickly?
Exactly! The structure allows common prefixes to be shared, reducing redundancy. Remember, in a trie, many words can be processed by traversing shared paths.
Efficiency of Tries
Unlock Audio Lesson
Let’s discuss why tries are efficient. Who can tell me the time complexity for searching a word in a trie?
It's O(length of the word), right?
Correct! What about space complexity? Is it higher or lower compared to other string storage methods?
I think it's higher because each character has to be stored in a node.
Right! While tries can consume more memory than, say, a simple array for unique strings, they excel in scenarios with many common prefixes, leading to overall reduced redundancy. Think of it as 'more nodes, more sharing'!
Comparison with Other Structures
Unlock Audio Lesson
How do tries compare to hash tables when it comes to storing strings?
Hash tables can be faster for lookups, but they don't handle prefixes like tries do, right?
That's a great observation! Tries allow for prefix-based operations, which is something hash tables don't inherently provide. Remember: 'Tries Triumph on Prefix Searches'!
So, if I wanted to build an autocomplete feature, a trie would be better?
Precisely! For operations involving shared prefixes, tries shine. Let's summarize: Tries are great for prefix searches and save space when many strings share common parts.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
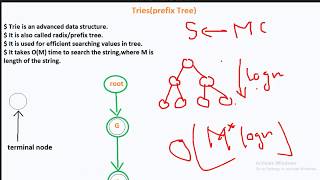
This section delves into the concept of tries, a special type of tree structure that allows for fast string lookups. Each node in a trie represents a character from a string, enabling efficient storage and retrieval while maintaining a time complexity related to the length of the strings.
Detailed
Detailed Summary
Tries, also known as prefix trees, are specialized tree structures used for storing strings in a way that promotes fast lookup operations. Each node in a trie corresponds to a character from the strings being stored. As a result, searching for a string in a trie is efficient, with a time complexity of O(length of the word). This characteristic makes tries particularly useful for applications like autocomplete systems and spell checking, where quick retrieval of information is paramount. The structure allows multiple strings to share common prefixes, which can lead to significant memory savings compared to storing each string individually. Overall, tries are a valuable addition to the family of data structures because they combine efficiency in space and time, making them ideal for handling a large set of string data.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of Tries
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A tree-based data structure for storing strings, used especially for autocomplete and spell checking.
Detailed Explanation
Tries, also known as prefix trees, are specialized tree-like data structures used for storing strings efficiently. Each node in a trie corresponds to a single character of a string, starting with the root node that signifies the beginning of a string. This hierarchical structure allows for efficient retrieval, organization, and management of strings, making it particularly useful in applications like autocomplete features in search engines or text processors.
Examples & Analogies
Imagine a library where books are organized by the first letter of their titles. Instead of searching through all the books, if you know the first letter, you can go to that section immediately. Similarly, tries take advantage of the common prefix shared by a set of strings (or words), allowing quick searches and retrievals based on that prefix.
Node Structure in Tries
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Each node represents a character of the string.
Detailed Explanation
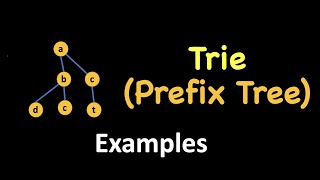
In a trie, each node can hold multiple child nodes, each representing a possible character following the character that the current node represents. This structure allows all the words that share the same prefix to branch off from a common node. For example, if 'cat' and 'car' are stored in a trie, the nodes would share the 'ca' prefix, with separate branches for 't' and 'r'.
Examples & Analogies
Consider a family tree where every member is connected by their last name. The last name connects all siblings, cousins, and relatives, who may branch off into different paths but share the same root. In the trie, the initial characters act like the last name, connecting multiple variations of words that share the same starting characters.
Lookup Efficiency
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Fast lookup: O(length of word)
Detailed Explanation
Lookups in tries are efficient because you can traverse the trie character by character. The time complexity for looking up a word in a trie is determined by the length of the word itself rather than the number of words stored in the trie. This means that even if the trie contains a vast number of words, searching for a word only takes time proportional to the number of characters in that word.
Examples & Analogies
Think about typing a word on your smartphone or computer. As you type the first few letters, suggestions for the complete word appear almost instantly. This quick suggestion process is like using a trie; it finds possible completions based on the characters you've typed, without having to look through every word in the dictionary.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Trie: A tree data structure used to efficiently store and retrieve strings.
-
Efficiency: Search operations in a trie have a time complexity of O(length of the word).
-
Applications: Tries are widely used in autocomplete and spell checking functionalities.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
For instance, a trie could store the words 'cat', 'cap', and 'can'. The node for 'c' will be shared among all three, leading to memory efficiency.
-
When a user types 'ca', the trie can immediately return all strings starting with that prefix by traversing down the shared path.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Tries aid your search, swift and spry, sharing paths where letters lie.
📖 Fascinating Stories
-
Imagine a library where every book is organized by the first letter, leading to each section of the library. The first letter leads you to a 'T' for Tries, helping you find your book quickly as you traverse the aisles.
🧠 Other Memory Gems
-
To remember the uses of tries, think 'CAPS': C for check spelling, A for autocomplete, P for prefix search, S for storing strings.
🎯 Super Acronyms
FAST
- Find And Search Trie for quick lookup.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Trie
Definition:
A tree-based data structure used for storing strings, where each node represents a character of the string.
-
Term: Prefix
Definition:
A preceding segment of a string; multiple strings may share common prefixes, allowing for more efficient storage.
-
Term: Autocomplete
Definition:
A feature that predicts the rest of a word or phrase as users type.
-
Term: Spell Checking
Definition:
The process of verifying the spelling of words, often using a dictionary data structure like a trie.