Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Basic Concepts of Graphs
Unlock Audio Lesson
Today, we're exploring graphs. Can anyone tell me what a graph consists of?
A graph consists of vertices and edges.
Correct! Vertices are the nodes, and edges are the connections between them. We also have different types of graphs. Who can name one?
Directed and undirected graphs!
That's right! In directed graphs, edges have a direction, while undirected graphs do not. Let's remember this with the acronym DUE: 'Directed' for edges with direction and 'Undirected' for edges without direction.
What are weighted graphs?
Great question! A weighted graph has edges that have weights representing some kind of cost or distance. Remember this concept by thinking of 'weights' like the cost of a ticket for a bus route! So, what are the main types of graphs so far?
We have directed, undirected, weighted, and unweighted graphs!
Excellent summary, everyone! These classifications help us determine how we can use these graphs in real-world applications.
Graph Representation
Unlock Audio Lesson
Now, let's talk about how we can represent graphs. Can anyone explain what an adjacency matrix is?
It's a 2D array where each entry shows whether there is an edge between two vertices.
Exactly! If there’s an edge between vertex i and j, then matrix[i][j] equals 1, otherwise it equals 0. How about the space complexity of creating such a matrix?
It’s O(V²) because you need to maintain a value for every pair of vertices.
Correct again! Now let's compare that with the adjacency list. Who can explain what that is?
An adjacency list stores each vertex with a list of adjacent vertices, which makes it more space-efficient.
Very well said! The space complexity for an adjacency list is O(V + E). Now can you summarize the differences in representation?
Adjacency matrix is O(V²) and better for dense graphs, while adjacency lists are O(V + E) which is better for sparse graphs.
Exactly! Understanding these representations is crucial for implementing graph algorithms effectively.
Graph Traversal Techniques
Unlock Audio Lesson
Let's dive into graph traversal methods. Who can tell me about BFS?
BFS stands for Breadth-First Search, and it explores neighbors level by level using a queue.
Right! The complexity of BFS is O(V + E). And what about Depth-First Search, or DFS?
DFS explores as far down one branch before backtracking using a stack or recursion.
That's correct! It's also O(V + E). Let’s remember: BFS uses a queue for breadth, while DFS uses a stack for depth. Can anyone think of a real-world application of these traversals?
BFS could be used in social networks to find friends at a particular level!
Great example! Now, who can summarize key points about graph traversal techniques?
BFS explores level-wise and uses a queue, while DFS goes deep down one path using a stack.
Fantastic summary! Understanding these traversal techniques is vital for navigating graphs efficiently.
Applications of Graphs
Unlock Audio Lesson
Let’s discuss the applications of graphs. What are some of the uses of graphs in computer science?
They can be used for shortest path algorithms, like finding the best route on a map!
Yes! Shortest path algorithms like Dijkstra's and Bellman-Ford are excellent examples. What else?
Graphs help in cycle detection within networks!
Correct! Cycle detection can be crucial in various applications. What about topological sorting?
It’s used for organizing tasks in proper order, especially in project planning!
Excellent! So far, we’ve identified shortest paths, cycle detection, and topological sorting as key applications. Can anyone summarize the significance of graphs?
Graphs help model complex relationships between data and solve numerous real-world problems efficiently!
Perfectly summarized! Grasping the applications of graphs broadens our ability to tackle intricate problems.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section introduces graphs as a non-linear data structure composed of vertices and edges, detailing their types such as directed vs. undirected, weighted vs. unweighted, and cyclic vs. acyclic. The representation methods for graphs and their significance in various applications are also overviewed.
Detailed
Introduction to Graphs
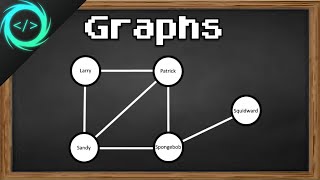
Graphs are fundamental non-linear data structures consisting of sets of vertices (or nodes) and edges that connect these vertices. They offer a powerful means of representing relationships between entities. Graphs can be classified in several ways:
- Directed vs Undirected: A directed graph has edges that have a direction (from one vertex to another), while an undirected graph has edges with no specified direction.
- Weighted vs Unweighted: Weighted edges carry a value (weight), which can represent costs, distances, or other measures, while unweighted edges do not.
- Cyclic vs Acyclic: Cyclic graphs have at least one cycle, a path where the starting and ending vertex is the same, whereas acyclic graphs do not.
Graph traversal techniques such as Breadth-First Search (BFS) and Depth-First Search (DFS) are critical for exploring these structures. Understanding the representations and applications of graphs—including shortest path finding, cycle detection, and other algorithmic applications—is essential for computer science, particularly in fields like networking, optimization, and artificial intelligence.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
What is a Graph?
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A graph is a non-linear data structure consisting of vertices (nodes) and edges (connections).
Detailed Explanation
A graph represents a collection of vertices and edges. Each vertex acts like a point in a network, and edges are the connections between these points. Unlike linear data structures, graphs can represent more complex relationships, such as those found in social networks or geographical maps.
Examples & Analogies
Think of a graph like a map of a city where intersections are the vertices and roads connecting those intersections are the edges. Just like you can move from one intersection to another via roads, you can travel between nodes on a graph through its edges.
Types of Graphs
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
It can be:
- Directed or Undirected
- Weighted or Unweighted
- Cyclic or Acyclic
Detailed Explanation
Graphs can be categorized based on the characteristics of their edges. In a directed graph, edges have a direction, indicating a one-way relationship between vertices. In contrast, undirected graphs have edges with no direction, representing a bidirectional relationship. Weighted graphs assign a value (weight) to each edge, which may represent distance or cost, while unweighted graphs treat all edges equally. Lastly, cyclic graphs contain loops, allowing a path that starts and ends at the same vertex, whereas acyclic graphs do not have such loops.
Examples & Analogies
Consider a directed graph like a one-way street sign, where traveling allows you to go in only one direction, while an undirected graph resembles a two-way street where you can travel both ways. A weighted graph could be compared to a map that shows the distance between locations, while an unweighted graph purely reflects where the locations are without distances.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Vertices: The individual nodes in a graph.
-
Edges: Connections between the vertices in a graph.
-
Directed Graph: A graph with edges that have a defined direction.
-
Undirected Graph: A graph without direction on its edges.
-
Weighted Graph: A graph with edges that carry a weight or cost.
-
Adjacency Matrix: A representation of a graph using a 2D array.
-
Adjacency List: A representation of a graph using a list of adjacent vertices.
-
Traversal: The process of visiting all the vertices in a graph.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of a directed graph: A city's one-way streets connecting intersections.
-
Example of a weighted graph: A map showing distances between cities where edges represent road lengths.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a graph you will find, vertices to connect, edges unconfined.
📖 Fascinating Stories
-
Imagine a city where each intersection is a vertex and roads are edges, some charging tolls as weights to travel them.
🧠 Other Memory Gems
-
To remember graph types: ‘DUE’ - Directed, Undirected, and Edge weights (Weighted).
🎯 Super Acronyms
In a graph
- 'VE'A - for Vertex and Edge Arrangement.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Graph
Definition:
A non-linear data structure consisting of vertices and edges.
-
Term: Vertex
Definition:
A node in a graph.
-
Term: Edge
Definition:
A connection between two vertices.
-
Term: Directed Graph
Definition:
A graph where edges have a specified direction.
-
Term: Undirected Graph
Definition:
A graph where edges do not have a specified direction.
-
Term: Weighted Graph
Definition:
A graph where edges have associated weights.
-
Term: Unweighted Graph
Definition:
A graph where edges do not have associated weights.
-
Term: Cyclic Graph
Definition:
A graph that has at least one cycle.
-
Term: Acyclic Graph
Definition:
A graph that does not contain any cycles.
-
Term: Adjacency Matrix
Definition:
A 2D array representing edges in a graph.
-
Term: Adjacency List
Definition:
A list where each vertex's adjacent vertices are stored.