Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Graph Traversal
Unlock Audio Lesson
Today, we’re diving into graph traversal methods. Can anyone tell me what graph traversal means?
Is it about how we can explore a graph structure?
Exactly! There are two main methods: Breadth-First Search and Depth-First Search. Let's start with BFS. Why do you think it uses a queue?
Because it needs to process all the nearest vertices first?
Perfect! BFS explores neighbors level by level, making it great for unweighted shortest path tasks.
Breadth-First Search (BFS)
Unlock Audio Lesson
BFS ensures we visit nodes layer by layer. Can you think of a real-world example where this might be useful?
Maybe like when navigating city streets to find the shortest route?
Exactly! In an unweighted graph of streets, BFS is optimal for finding direct connections. It has a time complexity of O(V + E).
What about the space complexity?
Good question! The space complexity also depends on O(V), as we need to store the vertices in the queue.
Depth-First Search (DFS)
Unlock Audio Lesson
Now let's discuss DFS. Why do you think we use recursion in DFS?
Maybe to follow one path as deeply as possible before backtracking?
Exactly! DFS explores one branch at a time, diving deep before coming back up. Are there situations where you'd prefer DFS over BFS?
It might be better for puzzles or problems where we need to explore many possibilities!
Absolutely! DFS can be more memory efficient, especially in sparse graphs. Its time complexity is also O(V + E).
Applications of BFS and DFS
Unlock Audio Lesson
Let’s wrap up by discussing applications of BFS and DFS. How do you think they’re used in practical scenarios?
BFS can find the shortest paths, and DFS might help in pathfinding in games!
Exactly! BFS is used in networking for routing data packets, while DFS is crucial for searching through mazes or tree-like structures.
Can these methods also help in detecting cycles in a graph?
Yes! Cycle detection often uses DFS, which can help identify circular paths. Understanding these traversals is foundational for graph algorithms.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section delves into two primary graph traversal techniques: Breadth-First Search (BFS) and Depth-First Search (DFS), detailing their methods, complexities, and applications, providing the foundation for various graph-related algorithms.
Detailed
Graph Traversal
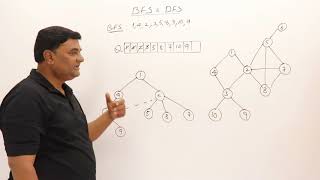
Graph traversal refers to the methods used to visit all the vertices of a graph in a systematic way. The two primary traversal techniques discussed in this section are Breadth-First Search (BFS) and Depth-First Search (DFS). Both methods differ in their approach and use cases, yet they offer foundational techniques for understanding more complex algorithms in graph theory.
Breadth-First Search (BFS)
BFS employs a queue data structure to explore a graph level by level, systematically visiting all neighbors of a vertex before moving on to the next level. This method is particularly effective for finding the shortest path in an unweighted graph or checking connectivity.
Time Complexity: O(V + E)
Key Features of BFS:
- Uses a Queue: Ensures that all vertices at the current level are explored before moving deeper.
- Explores Closest Vertices First: This makes it ideal for shortest-path problems in unweighted graphs.
Depth-First Search (DFS)
DFS, on the other hand, utilizes either a stack or recursion to dive deep into a graph, exploring as far as possible along a branch before backtracking. This method is advantageous for tasks that require exploring all possibilities.
Time Complexity: O(V + E)
Key Features of DFS:
- Uses a Stack or Recursion: Implements a last-in, first-out approach.
- Explores One Branch at a Time: More memory efficient than BFS in certain cases, especially in sparse graphs.
Overall, understanding BFS and DFS is critical as they serve as the backbone for many other algorithms operating on graphs, such as pathfinding, cycle detection, and network flow analysis.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Breadth-First Search (BFS)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Breadth-First Search (BFS):
- Uses a queue.
- Explores neighbors level by level.
- Time: O(V + E)
Detailed Explanation
Breadth-First Search (BFS) is an algorithm used to traverse or search through a graph. It works by exploring all of the neighbor vertices at the present depth before moving on to nodes at the next depth level. This approach is managed using a queue. When a node is visited, its adjacent vertices are added to the queue. BFS continues until there are no more nodes to visit, which means it has explored the entire graph.
Examples & Analogies
Think of BFS like a social media news feed. When you log in, you first see the posts from your friends (nodes) and their friends (neighbors), and as you scroll down, you explore posts from friends of friends, like a ripple effect. You're going layer by layer through your connections.
Depth-First Search (DFS)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Depth-First Search (DFS):
- Uses a stack or recursion.
- Explores one branch deeply before backtracking.
- Time: O(V + E)
Detailed Explanation
Depth-First Search (DFS) is another algorithm for traversing a graph but takes a different approach than BFS. In this method, the algorithm starts at a root node and explores as far as possible along each branch before backtracking. This can be achieved using a stack data structure or through recursion, where the function calls itself for each subtree down to the leaves.
Examples & Analogies
Imagine you're exploring a maze. You decide to go as deep as you can down a path until you hit a dead end. Then, you backtrack and try the next path. This method allows you to explore everything deeply before moving on to another section of the maze, similar to the way DFS operates in a graph.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Graph: A structure comprising vertices and edges for representing relationships.
-
Traversal: The process of visiting each vertex in a graph systematically.
-
BFS: A level-order traversal using a queue.
-
DFS: A traversal method using either a stack or recursion, exploring deep paths first.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Using BFS to find the shortest path in a maze where each cell represents a vertex.
-
Using DFS to navigate through a web of linked web pages, checking links exhaustively.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
For BFS, go layer by layer, / To find the shortest way, it's the player's prayer. / With DFS, dive deep and explore, / Through every path, until there's no more.
🎯 Super Acronyms
BFS - Best First Search for width; DFS - Deepest First Search for depth.
🧠 Other Memory Gems
-
To remember BFS, think 'Breadth' as in 'getting wide' and 'level', while for DFS, 'Depth' means going down deep.
📖 Fascinating Stories
-
Imagine a treasure hunt: BFS is your team that checks every room on the first floor before going to the next, while DFS sends one person deep into one room to search every corner.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: BreadthFirst Search (BFS)
Definition:
A graph traversal algorithm that explores the closest vertices first, using a queue.
-
Term: DepthFirst Search (DFS)
Definition:
A graph traversal algorithm that explores as deep as possible before backtracking, using a stack or recursion.
-
Term: Time Complexity
Definition:
The computational complexity that describes the amount of time an algorithm takes to run based on the input size.
-
Term: Space Complexity
Definition:
The amount of memory an algorithm uses in terms of the size of the input.
-
Term: Graph Traversal
Definition:
The process of visiting all the nodes in a graph in a systematic manner.