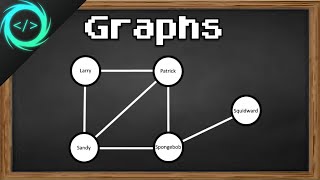
Representation of Graphs
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Adjacency Matrix
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's start with the adjacency matrix. Who can tell me what an adjacency matrix represents in a graph?

It shows the connections between vertices, right?

Exactly! It's like a table where both rows and columns are vertices. If there's an edge between two vertices, the entry in the matrix is '1'; if not, it's '0'. Can anyone tell me the space complexity of this representation?

Isn't it O(V²) where V is the number of vertices?

Correct! Now remember, it’s space-consuming for large graphs, especially if they're sparse. Here’s a mnemonic to remember its complexity: 'Massive matrix means a square space.'

What do you mean by sparse graphs?

Sparse graphs have relatively few edges compared to the possible maximum. The adjacency matrix can waste a lot of memory in those cases. So, which representation do you think is better for sparse graphs?

The adjacency list, right?

Great connection! Let’s summarize: the adjacency matrix is great for dense graphs, has a space complexity of O(V²), but isn’t ideal for sparse ones.
Adjacency List
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s move to another representation: the adjacency list. How does it differ from the adjacency matrix?

It only lists the neighboring vertices for each vertex instead of having a whole matrix.

Exactly! It’s efficient in terms of space, particularly for sparse graphs. Can someone tell me the space complexity here?

It’s O(V + E) because you consider both vertices and edges.

Perfect! Here’s a memory aid: think 'Less is More' for the adjacency list. Would you prefer the adjacency list or matrix for real-world applications, like social networks?

The adjacency list sounds better because social networks have many users but not every user is connected to every other.

Outstanding observation! Let’s cap this off: the adjacency list is space-efficient and better for sparse graphs, crucial for real-time applications.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
Graphs can be represented in different formats depending on their application. This section focuses on the adjacency matrix and adjacency list representations, explaining how each works, their advantages, and space requirements, which are crucial for effective utilization of graphs in algorithms.
Detailed
Detailed Summary
In the study of graphs, understanding how to represent them efficiently is fundamental to effectively solve problems utilizing graph algorithms. There are two primary representations of graphs: Adjacency Matrix and Adjacency List.
- Adjacency Matrix: This representation utilizes a 2D array where each cell [i][j] indicates whether an edge exists between vertex i and vertex j. The space complexity for this representation is O(V²), where V is the number of vertices. This format is efficient for dense graphs but can be memory intensive for sparse graphs.
- Adjacency List: In contrast, an adjacency list uses less memory for sparse graphs by maintaining a list of adjacent vertices for each vertex. This structure has a space complexity of O(V + E), where E is the number of edges. This makes adjacency lists a preferred choice for most real-world applications of graphs due to their efficiency with sparse data.
Understanding these representations is critical as they dictate the performance of graph-related algorithms such as traversal, shortest path computation, and others.
Youtube Videos








Audio Book
Dive deep into the subject with an immersive audiobook experience.
Adjacency Matrix
Chapter 1 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
- Adjacency Matrix:
- 2D array: matrix[i][j] = 1 if edge exists.
- Space: O(V²)
Detailed Explanation
An adjacency matrix is a way to represent a graph using a two-dimensional array. Each cell in the array corresponds to a pair of vertices in the graph. If there is an edge (a connection) between vertex i and vertex j, then matrix[i][j] is set to 1. If there is no connection, it is set to 0. The space complexity for an adjacency matrix is O(V²), where V is the number of vertices in the graph. This means that the amount of space used grows quadratically as the number of vertices increases.
Examples & Analogies
Think of an adjacency matrix like a seating chart for a large conference with multiple guests. Each row and column represents a guest, and if two guests know each other (there's a connection), a '1' is placed in the corresponding cell, indicating they can sit next to each other. If they don’t know each other, a '0' is in that cell.
Adjacency List
Chapter 2 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
- Adjacency List:
- Each vertex stores a list of adjacent vertices.
- Space: O(V + E)
Detailed Explanation
An adjacency list is another representation of a graph where each vertex has a list of other vertices it is connected to, rather than using a full matrix. This is done by creating an array of lists (or linked lists), where the index corresponds to the vertex and the list at that index contains the vertices that it is directly connected to. The space complexity for an adjacency list is O(V + E), where E is the number of edges. This is generally more space-efficient than the adjacency matrix, especially for sparse graphs (where there are relatively few edges compared to the number of vertices).
Examples & Analogies
Imagine organizing a group of friends for a movie night. Instead of writing a big chart (matrix) of who knows whom, you simply keep a contact list for each friend. For each friend, you write down only the names of friends who are also coming to the movie. This way, you have a concise list of who knows each other, which saves space and makes it easier to see connections.
Key Concepts
-
Adjacency Matrix: Represents graph edges in a two-dimensional array format, primarily beneficial for dense graphs.
-
Adjacency List: A more space-efficient representation for graphs, particularly effective for sparse data.
Examples & Applications
An adjacency matrix for a simple graph with 3 vertices and 2 edges might look like: [[0, 1, 1], [0, 0, 0], [0, 0, 0]].
An adjacency list for the same graph could be represented as: [ [1, 2], [], [] ] showing that vertex 0 connects to vertices 1 and 2.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
For dense graphs, a matrix is your place, to store all edges with ample space.
Stories
Imagine two neighbors, one invites everyone in for tea (adjacency matrix) while the other just invites close friends (adjacency list); who has more room?
Memory Tools
Remember 'MM' for Matrices Mean more Memory - the adjacency matrix needs more space than adjacency lists!
Acronyms
V + E
'Vertices and Edges'
the key to remember for the adjacency list’s efficiency.
Flash Cards
Glossary
- Adjacency Matrix
A 2D array representation of a graph where matrix[i][j] indicates if an edge exists between vertices i and j.
- Adjacency List
A data structure where each vertex stores a list of adjacent vertices representing the edges of a graph.
Reference links
Supplementary resources to enhance your learning experience.
