Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Heaps
Unlock Audio Lesson
Today, we're going to learn about heaps, a fundamental data structure used for priority queues. Who can explain what a priority queue is?
Isn't a priority queue where you can insert elements and always get the highest or lowest priority element first?
Exactly! A priority queue allows us to efficiently access the highest or lowest priority item. In heaps, we can have a Min-Heap or Max-Heap based on the priority rules. Who can tell me the difference?
In a Min-Heap, the smallest element is on top, while in a Max-Heap, the largest element is at the top.
Correct! Remember that Min-Heap ensures that each parent is less than or equal to its children. Let's also look at how we perform operations on heaps. What do you think insertion involves?
When you insert, you might need to reorder the heap to keep the properties intact, right?
Right again! The insertion operation takes O(log n) time because we must maintain the complete tree structure. Let's summarize: heaps are useful for priority queues with structured insertion and extraction operations.
Heap Operations
Unlock Audio Lesson
Now that we've introduced heaps, let's dive into their operations, including insertion and extraction. Can anyone describe how we would extract the minimum element from a Min-Heap?
We remove the root and then rearrange the tree, right?
Yes! After removing the root, we replace it with the last node and then 'heapify' downwards to maintain the heap structure. This operation also takes O(log n) time. Can someone tell me about how we build a heap from an array?
You can do that in O(n) time using a method called 'sift down' or heapifying the elements.
That's right! It’s efficient to build heaps from unsorted data. So, let's recap: heap operations have specific time complexities—insert and extract take O(log n), while building a heap is O(n).
Applications of Heaps
Unlock Audio Lesson
Let’s move on to where heaps are used in real-world applications. Can anyone think of an application where heaps are crucial?
What about heap sort? It uses heaps to sort elements, right?
Correct! Heap sort is a great example of how heaps can organize data efficiently. How does it work?
First, you build a heap and then repeatedly extract the maximum or minimum until the heap is empty.
Excellent! Besides heap sort, heaps are also important in Dijkstra’s algorithm for finding the shortest path. Who can explain how heaps help in that context?
Heaps keep track of the shortest distances efficiently, allowing you to always fetch the next closest vertex quickly.
Exactly! Heaps optimize the performance of Dijkstra’s algorithm. In summary, heaps are not just theoretical; they are widely used in practical algorithms like sorting and pathfinding.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
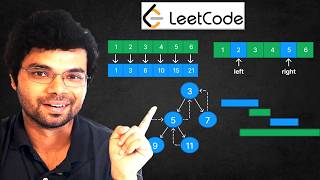
Heaps are specialized binary trees with a structure that facilitates efficient priority queue operations such as insertion and extraction of the minimum or maximum element. The section outlines the characteristics of Min-Heaps and Max-Heaps, the time complexities of operations on heaps, and their applications in algorithms such as Heap Sort and Dijkstra's algorithm.
Detailed
Heaps
Heaps are a type of complete binary tree that are particularly useful for implementing priority queues. They have two main types:
- Min-Heap: In a Min-Heap, the parent nodes are smaller than or equal to their children, ensuring that the smallest element is always at the root.
- Max-Heap: Conversely, in a Max-Heap, the parent nodes are larger than or equal to their children, placing the largest element at the root.
Operations on Heaps:
- Insert: Inserting a new element into the heap takes O(log n) time due to the necessity of maintaining the heap property when adding new elements.
- Extract-Min/Max: Removing the minimum or maximum element also takes O(log n) time because of the reorganization of the heap that follows the removal operation.
- Build-Heap: The process of building a heap from an unordered array can be accomplished in O(n) time.
Applications of Heaps:
- Heaps play a crucial role in Heap Sort, which offers an efficient method of sorting elements.
- They are also used in Dijkstra's algorithm for finding the shortest path in graphs, leveraging the priority queue characteristics of heaps.
In summary, heaps are essential data structures that enable high-performance data management in various computational algorithms.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of a Heap
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A heap is a complete binary tree used to implement priority queues.
Detailed Explanation
A heap is a specific type of data structure that is organized as a complete binary tree. This means that every level of the tree, except possibly for the last, is fully filled. The heap is particularly useful for implementing priority queues, which are data structures where each element has a priority level. The main characteristic of a heap is that it maintains a particular order in the nodes, either by value or priority.
Examples & Analogies
Imagine a line of people waiting for a bus, where one person is holding a sign indicating their priority (like an administrator). Everyone else has to wait according to their assigned priority. The administrator will always be served first, just like the heap structure prioritizes the parent node over its children.
Types of Heaps
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Min-Heap: Parent ≤ children
• Max-Heap: Parent ≥ children
Detailed Explanation
Heaps come in two main varieties: Min-Heaps and Max-Heaps. In a Min-Heap, the value of each parent node is less than or equal to the values of its child nodes. This ensures that the smallest value is always at the root of the heap. In contrast, a Max-Heap has the property that the value of each parent node is greater than or equal to the values of its child nodes, placing the largest value at the root.
Examples & Analogies
Think of a Min-Heap as a priority queue for emergency responders. The least critical case (like a sprained ankle) needs to be addressed after the most critical case (like a heart attack). In a Max-Heap, it's the opposite. Consider a sports tournament where the team with the most points (or best ranking) gets the top spot in the league, showing the hierarchy of performance.
Heap Operations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Operations:
• Insert: O(log n)
• Extract-Min/Max: O(log n)
• Build-Heap: O(n)
Detailed Explanation
Heaps support several important operations. Inserting an element into a heap takes O(log n) time, which means it becomes slower as the number of elements increases, but remains efficient. Extracting the minimum from a Min-Heap or the maximum from a Max-Heap also takes O(log n) time, as this requires restructuring the heap to maintain its properties. Building a heap from an unsorted array is more efficient, taking O(n) time because it cleverly organizes the elements with fewer comparisons than repeated insertions would require.
Examples & Analogies
Imagine a filing system for a large company. If you need to file a new document (insert operation), you will take some time to find the right spot, but because of the organization, finding the right place is faster than reorganizing the entire system. When you need to retrieve the most urgent document (extract operation), finding it might take time to ensure everything stays organized, but it is still much quicker than starting from scratch, similar to how heaps operate.
Applications of Heaps
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Used in Heap Sort and Dijkstra’s algorithm.
Detailed Explanation
Heaps have practical applications that extend into many areas of computer science. One of the most notable uses of heaps is in Heap Sort, a popular sorting algorithm that takes advantage of the heap structure to sort elements efficiently. Additionally, heaps are used in Dijkstra’s algorithm, which finds the shortest path in weighted graphs. The ability to quickly access the minimum element is key to efficiently implementing these algorithms.
Examples & Analogies
Think of Dijkstra’s algorithm as navigating through a city with several routes. If you always start from the point that has the shortest distance to your destination (like having a map that shows which roads are fastest), you will reach your goal more effectively. Similarly, heaps allow programmers to manage priorities efficiently, leading to better performance in tasks like sorting kids in a game based on their scores or finding the most efficient route in mapping applications.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Heap: A complete binary tree structure used for implementing priority queues.
-
Min-Heap: A type of heap that ensures the parent node is less than or equal to its children.
-
Max-Heap: A type of heap that ensures the parent node is greater than or equal to its children.
-
Operations: Insert and Extract-Min/Max operations are performed in O(log n) time.
-
Build-Heap: Constructing a heap from an array takes O(n) time.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
When implementing a priority queue, using a Min-Heap allows you to consistently retrieve the smallest element, such as in scheduling tasks that have deadlines.
-
Dijkstra's algorithm benefits from heaps when it maintains a priority queue for unvisited nodes while finding the shortest path through a graph.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
For heaps that help us sort, parenting is of main court; Min up high, Max is chief, order flows like a leaf.
📖 Fascinating Stories
-
Once in a forest of trees, a Min-Heap ruled where the smallest of fruits hung on the top, fostering growth as fruit fell below. Each round of picking led to a bountiful harvest, but a Max-Heap said, 'I won't let the largest go!' This tale teaches how both protect their own in heaps.
🧠 Other Memory Gems
-
Think of 'H.E.A.P.' - Hierarchical, Efficient, Array, Priority to remember key aspects of heaps.
🎯 Super Acronyms
For Heaps, remember 'M.I.E.' - Min/Max, Insert, Extract to understand their main operations.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Heap
Definition:
A complete binary tree used to implement priority queues.
-
Term: MinHeap
Definition:
A type of heap where the parent node is less than or equal to its children.
-
Term: MaxHeap
Definition:
A type of heap where the parent node is greater than or equal to its children.
-
Term: Insert
Definition:
Operation to add a new element into the heap.
-
Term: ExtractMin/Max
Definition:
Operation to remove the minimum or maximum element from the heap.
-
Term: BuildHeap
Definition:
Operation to construct a heap from an unordered array.