Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.

Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.

Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
What is Admittance?
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Today, we will discuss admittance in parallel RLC circuits. Admittance, denoted by 'Y', is the inverse of impedance, which indicates how easily a circuit allows current to flow.

So, is higher admittance better for current flow?

Exactly! A higher admittance means lower impedance. This is crucial for ensuring that your circuits perform efficiently. Remember, Y is calculated using the formula: Y = 1/R + 1/jωL + jωC.

What does each part of the formula represent?

Good question! R is the resistance, L is inductance, and C is capacitance. Each of these components affects how the circuit takes up current at different frequencies. Let's keep this in mind as we move along!

In summary, admittance is a measure of current flow capability. We will explore its implications further!
Calculating Total Admittance
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Now, let's calculate the total admittance. The formula we discussed is Y = 1/R + 1/jωL + jωC. Why do you think we need to add these components?

Because they have different forms of impedance contributing to the overall effect?

Exactly! Each component offers its own contribution to the overall admittance. Let’s take a sample circuit. If R is 50Ω, L is 10mH, and C is 100μF, how would we go about finding the total Y?

First, we calculate each term: 1/R, then for 1/jωL and jωC. We would need the frequency to find ω.

Correct! By substitution, you can find the total admittance. Remember to practice as it’s vital for real-world circuit analysis!
Understanding Magnitude and Phase of Admittance
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

We’ve now calculated total admittance. Next, let’s explore magnitude and phase, expressed as |Y| = √[(1/R)² + (ωC - 1/ωL)²]. Who can explain why the magnitude is important?

It tells us how much current can flow at different frequencies, right?

Very well put! The phase reveals how the current relates to the voltage, providing crucial information for tuning circuits. Understanding these two aspects allows engineers to design effective filters.

How would we use phase in practical situations?

That's a great inquiry! Phase helps in adjusting circuit elements to achieve desired frequency responses. It ensures that our signals synchronize correctly.

So remember, both magnitude and phase provide invaluable insights into how circuits behave!
Applications of Admittance Analysis
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Lastly, let's talk about the applications of admittance analysis. Can someone suggest a scenario where knowing admittance is critical?

In tuning radio circuits, right? To select the right frequency!

Correct! It's essential in many devices, ensuring signals can be transmitted without distortion. Whether it's in filters or signal processing, achieving the right admittance affects overall circuit performance.

Also, what about impedance matching? Is that related?

Absolutely! Impedance matching often involves optimizing admittance to ensure maximum power transfer. Great connection there!

In summary, admittance analysis has vast applications both in theory and practice, vital for effective circuit design.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In the Admittance Analysis section, we examine the total admittance for a parallel RLC circuit. Key formulas are introduced, including the expression for total admittance, its magnitude, and phase. Understanding these concepts is vital for analyzing resonance conditions in circuits.
Detailed
Admittance Analysis
In this section, we focus on the admittance analysis of parallel RLC circuits, a critical aspect for understanding how these circuits behave under various frequency conditions. Admittance, represented as Y, is the measure of how easily a circuit allows current to flow and is defined as the inverse of impedance.
Total Admittance
The formula for total admittance in a parallel RLC circuit is given by:
$$Y = \frac{1}{R} + \frac{1}{jωL} + jωC$$
In this equation:
- Y is the total admittance,
- R is resistance,
- L is inductance,
- C is capacitance,
- ω is the angular frequency (radians per second).
Magnitude and Phase of Admittance
The magnitude and phase of the admittance can be calculated as:
$$|Y| = \sqrt{\left(\frac{1}{R}\right)^2 + \left(ωC - \frac{1}{ωL}\right)^2}$$
This expression highlights how the reactive components (inductance and capacitance) influence overall circuit behavior. The phase angle can also be drawn from the admittance values, thus providing insights into current and voltage relations in the circuit.
Understanding these parameters is essential for engineers and technologists working with circuits to manage how they respond to oscillations and resonance, facilitating filter design and tuning applications.
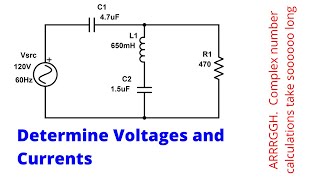
Youtube Videos



Audio Book
Dive deep into the subject with an immersive audiobook experience.
Total Admittance (Y)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The total admittance (Y) of a parallel RLC circuit is given by:
\[ Y = \frac{1}{R} + \frac{1}{jωL} + jωC \]
Detailed Explanation
Admittance is a measure of how easily a circuit allows current to flow when a voltage is applied. It is the reciprocal of impedance. In a parallel RLC circuit, the total admittance (Y) is calculated by adding the admittance of each component: the resistor (\(\frac{1}{R}\)), the inductor (\(\frac{1}{jωL}\)), and the capacitor (\(jωC\)). Here, 'j' represents the imaginary unit, which accounts for the phase difference between voltage and current in reactive components. The terms contribute differently: the resistor dissipates power, while the capacitor and inductor store energy.
Examples & Analogies
Think of admittance like a water faucet. The more open the faucet (the lower the resistance), the more water (current) can flow through it. Each component in the circuit behaves like a different type of faucet, with the resistor opening more readily, while the inductor and capacitor have phase relationships that can either help or hinder the flow depending on the frequency of operation.
Magnitude and Phase
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The magnitude and phase of the total admittance can be calculated as:
\[ |Y| = \sqrt{\left(\frac{1}{R}\right)^2 + \left(ωC - \frac{1}{ωL}\right)^2} \]
Detailed Explanation
The magnitude of the admittance (\(|Y|\)) gives us the effective amount of current that can flow through the circuit for a given voltage. This formula shows how to calculate the magnitude by taking the square root of the sum of the squares of both the resistive and reactive components. The reactive component combines the effects of the capacitor and inductor, with their contributions depending on the frequency (\(ω\)). Understanding how these parameters interact helps us predict the circuit's behavior in frequency domain.
Examples & Analogies
Imagine you are trying to find the total flow of various streams into a lake. Each stream has a different width (like resistance) and flow speed (like the reactance from capacitance and inductance). To find the total flow, you assess each stream and combine their contributions, eventually leading to the overall flow (or admittance) into the lake.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Total Admittance: Calculated as Y = 1/R + 1/jωL + jωC, representing the total ease of current flow.
-
Magnitude and Phase: Essential measures derived from admittance that indicate circuit behavior in response to frequency.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a parallel RLC circuit with R = 100Ω, L = 5mH, and C = 20μF, the total admittance can be computed to determine how the circuit handles specific frequencies.
-
By understanding the magnitude and phase of admittance, engineers can design better filters for audio electronics, ensuring consistent sound quality.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When admittance is high, current will fly, but when it's low, it's time to say goodbye.
📖 Fascinating Stories
-
Imagine a river (current) flowing through cities (circuit components); admittance is like the bridges (impedances) that help the river reach each city efficiently.
🧠 Other Memory Gems
-
Remember 'Y = 1/R + 1/jωL + jωC' as 'You are Ready - Join waves of Currents'.
🎯 Super Acronyms
To recall the components impacting admittance, think of 'RCL' for Resistance, Capacitance, and Inductance leading to effective current flow.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Admittance
Definition:
A measure of how easily a circuit allows current to flow, represented as the inverse of impedance.
-
Term: Impedance
Definition:
The total opposition a circuit presents to alternating current, comprising both resistance and reactance.
-
Term: Magnitude
Definition:
The absolute value of admittance that indicates the amount of current flow capacity at a certain frequency.
-
Term: Phase
Definition:
The angle difference between voltage and current waveforms in an AC circuit.

