Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.

Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.

Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Average Power Dissipation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Today we are discussing power dissipation in RLC circuits. Can anyone tell me what is meant by average power?

Is it the total power used by the circuit over time?

That's close! Average power refers to the power that is dissipated as heat in resistors during a complete cycle. It can be calculated using the formula P_avg = (1/2) * I_rms² * R.

What does I_rms stand for?

Good question! I_rms stands for root mean square current. It represents the effective value of the alternating current in the circuit.
Relation of Current and Power
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Now that we know how to calculate average power, what do you think happens to power dissipation if the current increases?

Doesn't higher current mean more power?

Exactly! Power dissipation is proportional to the square of the current, which is why maintaining optimal current levels is crucial.

And what about resistance? How does it factor in?

Resistance works as a limiting factor. Higher resistance means less current for the same voltage, reducing power dissipation.
Practical Applications of Power Calculation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Why do you think calculating power dissipation is important in circuit design?

It helps prevent overheating, right?

Exactly! If we don't calculate it, components may fail if they exceed their thermal limits. Calculating power dissipation helps ensure safety and efficiency!

Are there any safety devices involved?

Yes, fuses and circuit breakers are used to disconnect circuits when excessive power is detected, providing safety against risks.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
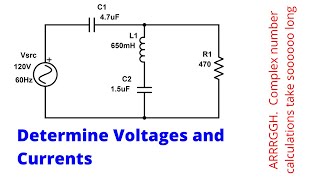
Power dissipation in RLC circuits is a critical parameter, measured as the average power across resistances in the circuit. The formula provided shows how to compute average power based on the RMS current and resistance.
Detailed
In this section, we examine the concept of power dissipation in RLC circuits, specifically focusing on how resistive components dissipate energy in the form of heat. The average power dissipation is given by the equation P_avg = (1/2) * I_rms² * R, where I_rms is the root mean square of the current flowing through the resistive element and R is the resistance. Understanding power dissipation is essential for circuit design, ensuring components do not overheat and cause failures. This formula shows the direct relationship between current and power, highlighting the significance of properly managing current levels to optimize performance and reliability in electrical circuit design.
Youtube Videos



Audio Book
Dive deep into the subject with an immersive audiobook experience.
Average Power Formula
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The average power is given by the formula:
$$
P_{avg} = \frac{1}{2}I_{rms}^2R
$$
Detailed Explanation
The average power dissipated in a resistor within an RLC circuit can be calculated using the formula P_avg = (1/2) * I_rms² * R. Here, I_rms is the root mean square value of the current flowing through the resistor, and R is the resistance value in ohms. This formula is derived from the fact that power in electrical circuits is related to the voltage and current, particularly how they interact in resistive components.
Examples & Analogies
Think of a light bulb connected to a power source. The amount of light it emits corresponds to the power it dissipates. In this context, the average power formula helps us understand how a specific current flowing through a bulb (like I_rms) affects the brightness (power) based on the bulb's resistance (R).
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Power Dissipation: The process by which electrical energy is converted into heat energy within a circuit's resistive components.
-
Average Power (P_avg): The mean power dissipated over a specified period in a circuit.
-
Root Mean Square Current: A value expressing the effective current that can be expected to produce the same power as a DC current.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
If a circuit has a resistance of 50 ohms and the RMS current is 2 A, the average power dissipation can be calculated as P_avg = (1/2) * (2^2) * 50 = 100 W.
-
In a circuit where the effective current is doubled, power dissipation increases by a factor of four given that power is proportional to the square of the current.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
For current, if it's large, power takes a charge, double it up, and power's up, but be careful, watch your sparks!
📖 Fascinating Stories
-
Imagine a circuit at a festival, where the resistance is like a bouncer controlling the crowd. If too many people (current) come in, they could overheat the dance floor (power dissipation). Keep the balance for a great party!
🧠 Other Memory Gems
-
Acronym P=IR² for remembering Power = I squared times Resistance.
🎯 Super Acronyms
PIRC = Power = I² * R Current.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Average Power
Definition:
The mean value of power dissipated over a defined interval of time, by resistive elements in a circuit.
-
Term: I_rms
Definition:
Root mean square value of current, reflecting the effective value of an AC current.
-
Term: Resistance (R)
Definition:
The opposition offered by a resistor to the flow of electric current.

