Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.

Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.

Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Series RLC as Bandpass Filter
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Today we're going to learn about how a Series RLC circuit can function as a bandpass filter. Can anyone tell me what a bandpass filter does?

It allows only a certain range of frequencies to pass through.

Exactly! In the context of a Series RLC circuit, we need to understand the relationship between voltage across the resistor and the total impedance. The formula for the voltage across the resistor is given by \( \frac{V_R}{V_{in}} = \frac{R}{Z} \). What do you think Z represents?

Z is the total impedance of the circuit, which includes the resistance, inductance, and capacitance!

Spot on! This impedance will change with frequency, affecting the voltage across our resistor. Now, let’s summarize the importance of this formula in identifying the functioning of the bandpass filter.
Understanding Bandwidth
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Next, let’s discuss bandwidth. Can someone explain what bandwidth means in the context of our filter?

It's the range of frequencies that the filter allows through.

Correct! The bandwidth can be calculated using the formula \( BW = f_2 - f_1 = \frac{R}{2\pi L} \). What does each symbol represent here?

R is the resistance and L is the inductance, but what are \( f_1 \) and \( f_2 \)?

Good question! \( f_1 \) and \( f_2 \) represent the lower and upper cutoff frequencies, respectively. The bandwidth indicates how wide our bandpass is. Can you think of why knowing this is important?

It helps in designing circuits for communication systems!

Exactly! Knowing the bandwidth enables engineers to fine-tune circuit performance.
Applications of Series RLC Bandpass Filter
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Now, let’s reflect on applications of RLC circuits as bandpass filters. Can anyone provide an example?

I think they are used in radios to select specific frequencies!

Exactly! They are crucial in tuning circuits for radios or other signal processing devices. Knowing how they operate at specific frequencies is essential for effective design. Can someone summarize the key takeaways from today's discussion?

We learned that variances in impedance affect voltage across the resistor and that bandwidth determines the filter's frequency range.

Great summary! Understanding these concepts is vital for applying RLC circuits in real-world scenarios.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The Series RLC circuit is analyzed as a bandpass filter, focusing on the voltage across the resistor, and introduces the concept of bandwidth defined as the difference between the upper and lower frequency limits at which the circuit effectively passes signals.
Detailed
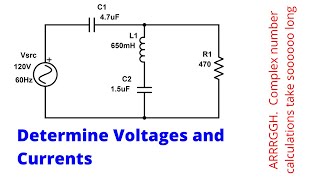
Series RLC as Bandpass Filter
This section addresses how a Series RLC circuit can act as a bandpass filter, allowing signals within a specific frequency range to pass while attenuating others. The voltage across the resistor forms the basis of understanding the circuit's behavior, represented by the formula:
$$\frac{V_R}{V_{in}} = \frac{R}{Z}$$, where Z denotes the total impedance of the circuit. The bandwidth is another crucial aspect detailed by the equation:
$$BW = f_2 - f_1 = \frac{R}{2\pi L}$$. This describes the frequency range where the bandpass filter operates effectively. Understanding these properties is key for applications such as signal processing and communication systems.
Youtube Videos



Audio Book
Dive deep into the subject with an immersive audiobook experience.
Voltage Across R
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The voltage across the resistor (R) in a series RLC circuit can be expressed as:
\[
\frac{V_R}{V_{in}} = \frac{R}{Z}
\]
Detailed Explanation
This equation describes how the voltage across the resistor (denoted as V_R) relates to the input voltage (V_in) and the total impedance of the circuit (Z). Impedance (Z) is the total opposition to the flow of current in the circuit, combining resistance (R), inductive reactance, and capacitive reactance. A high value of R or a low value of Z will increase the voltage across the resistor relative to the input voltage, meaning that more of the input voltage is observed at the resistor.
Examples & Analogies
Think of the series RLC circuit as a water system: V_in is the water pressure from a tank, and R is a narrow pipe that restricts the flow. If the total 'resistance' of the whole system (which includes other pipes and valves, analogous to Z) is high, then less pressure (voltage) reaches the narrow pipe (resistor). In contrast, if Z is lower, then more pressure is available to the narrow pipe.
Bandwidth Calculation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The bandwidth of a series RLC bandpass filter is calculated as:
\[
BW = f_2 - f_1 = \frac{R}{2\pi L}
\]
Detailed Explanation
Bandwidth (BW) in the context of a bandpass filter refers to the range of frequencies that can effectively pass through the filter. The formula indicates that bandwidth is directly proportional to resistance (R) and inversely proportional to the inductance (L). In simpler terms, increasing R allows a wider range of frequencies to pass, while increasing L narrows the range. This characteristic defines how selective or broad the filter is in allowing frequency signals.
Examples & Analogies
Consider a filter as a set of train tracks. If the tracks (inductance L) are narrow, only a few trains (frequencies) can pass at once. If you widen the tracks (reduce L), more trains can share the tracks simultaneously, thus increasing the bandwidth. However, if you block off parts of the track (increase R), less traffic is allowed through, creating a narrower selection of trains that can pass.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
RLC Circuit: Consists of a resistor, inductor, and capacitor influencing current and voltage.
-
Impedance (Z): A measure of total opposition to current that combines resistance and reactance.
-
Voltage Output: Described by \( \frac{V_R}{V_{in}} = \frac{R}{Z} \).
-
Bandwidth (BW): The frequency range that the bandpass filter allows, calculated with \( BW = f_2 - f_1 = \frac{R}{2\pi L} \).
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a radio receiver, the Series RLC circuit tunes into specific frequencies to allow clear signal reception while blocking others.
-
In an audio system, a Series RLC bandpass filter is used to enhance certain frequency ranges for optimal sound quality.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a circuit with R, L, and C, a bandwidth is the key to free signals you see!
📖 Fascinating Stories
-
Imagine a radio station tuning in. It captures the best sound by filtering out the noise, just like how a bandpass filter selects specific frequencies to deliver clear, beautiful music.
🧠 Other Memory Gems
-
To remember the bandwidth formula, think 'R over L by 2 pi is the style for quality.'
🎯 Super Acronyms
Bandpass Filter
- B.F. - Bear Frequency
- allow passing!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: RLC Circuit
Definition:
An electrical circuit composed of a resistor (R), an inductor (L), and a capacitor (C) connected in series or parallel.
-
Term: Impedance (Z)
Definition:
The total resistance that a circuit presents to alternating current, comprising resistance and reactance.
-
Term: Voltage Divider
Definition:
A circuit where the output voltage is a fraction of its input voltage, determined by the resistance values.
-
Term: Bandwidth (BW)
Definition:
The range of frequencies that a filter allows to pass through; calculated as the difference between upper and lower cutoff frequencies.
-
Term: Cutoff Frequency
Definition:
The frequency at which the output of the filter falls to a specific fraction (usually -3 dB) of the input signal.

