Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.

Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.

Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Basic Configuration of Parallel RLC Circuits
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Today, we are diving into the world of parallel RLC circuits. Who can tell me what we mean by a parallel configuration?

Is it when all components are connected along the same pathway?

Not quite. In a parallel configuration, components are connected across the same voltage source. This allows each component to have its path. Imagine multiple roads leading to a single destination.

So, if one component fails, the others can still operate, just like an alternate route in a road system?

Exactly! Great analogy! Remember to visualize this when thinking about circuit configurations.
Admittance Analysis of Parallel RLC Circuits
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Now, let's discuss admittance in parallel circuits. Can anyone explain why we prefer admittance over impedance here?

Isn't impedance just the opposite? Admittance shows how easily current flows?

That's right! Admittance is indeed the reciprocal of impedance, and it's more intuitive when analyzing branches in parallel circuits. The formula is: Y = 1/R + 1/jωL + jωC.

What does each part represent in the formula?

Good question! Each term reflects how resistive, inductive, and capacitive elements contribute to current flow balance in the circuit.
Resonance Conditions in Parallel RLC Circuits
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Next, let's explore resonance in this circuit. Can anyone tell me the formula for the resonant frequency?

$$ω_0 = \frac{1}{\sqrt{LC}}$$.

Excellent! This means both the inductor and capacitor values will determine the frequency. How does this relate to the quality factor?

The quality factor shows how selective the circuit is, right? Higher Q means a narrower bandwidth?

Correct! The quality factor is calculated as $$Q = R\sqrt{\frac{C}{L}}$$. This helps us assess how underdamped the circuit is and its resonant behavior.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we delve into parallel RLC circuits, examining their basic configuration, total admittance, effects of resonance, and related parameters. Key equations for admittance and quality factors are provided to explain circuit behavior.
Detailed
Parallel RLC Circuits
Parallel RLC circuits consist of resistors (R), inductors (L), and capacitors (C) connected in a parallel configuration. The basic configuration can be illustrated as follows:
┌─R─┐ V_in ─┼─L─┼─┐ └─C─┘ │ GND
In analyzing parallel circuits, we utilize admittance (Y) instead of impedance. The total admittance can be expressed mathematically as:
$$
Y = \frac{1}{R} + \frac{1}{jωL} + jωC
$$
Understanding the total admittance is critical for analyzing how these circuits behave under varying frequencies.
One of the intriguing features of parallel RLC circuits is their resonant frequency, which is the same as in series circuits:
$$
ω_0 = \frac{1}{\sqrt{LC}}
$$
This means that the resonant frequency is determined by the values of L and C, demonstrating that resonance is a fundamental characteristic of RLC circuits. Additionally, the quality factor (Q), which provides insight into the selectivity of the resonant frequency, can be calculated as:
$$
Q = R\sqrt{\frac{C}{L}}
$$
The quality factor indicates how underdamped the circuit is, impacting its bandwidth, which can be critical in applications like tuning and filtering. Proper understanding and application of these principles allow engineers to design circuits effectively for their desired functionalities.
Youtube Videos

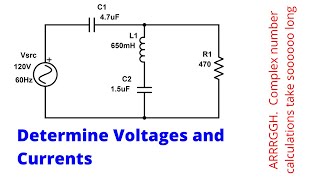


Audio Book
Dive deep into the subject with an immersive audiobook experience.
Basic Configuration
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
┌─R─┐ V_in ─┼─L─┼─┐ └─C─┘ │ GND
Detailed Explanation
In this chunk, we see the basic configuration of a Parallel RLC circuit. It consists of three main components: a resistor (R), an inductor (L), and a capacitor (C). In this configuration, the voltage source (V_in) is applied across all three elements, which are connected in parallel. This means that each component has the same voltage across it while allowing different currents to flow through them based on their reactance and resistance.
Examples & Analogies
Think of a Parallel RLC circuit like a traffic intersection where multiple roads (R, L, and C) meet at a central point (the voltage source). Each road can allow different numbers of vehicles (current) to travel through based on traffic rules (their individual impedances), but they all share the same signal (voltage) controlling when to go.
Admittance Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Total Admittance (Y):
\[ Y = \frac{1}{R} + \frac{1}{jωL} + jωC \]
- Magnitude and Phase:
\[ |Y| = \sqrt{\left(\frac{1}{R}\right)^2 + \left(ωC - \frac{1}{ωL}\right)^2} \]
Detailed Explanation
Admittance (Y) is the reciprocal of impedance and represents how easily complex currents can flow through a circuit. In a Parallel RLC circuit, we calculate the total admittance by summing the admittances of the resistor, inductor, and capacitor. Each component contributes differently, depending on whether they are resistive or reactive. The magnitude of the total admittance gives us an understanding of how easily current flows in the circuit at different frequencies, which involves determining the net effect of the capacitive and inductive reactances.
Examples & Analogies
Imagine a water park with multiple slides (the resistor, inductor, and capacitor). Each type of slide offers different challenges to navigate (impedance). The admittance is like measuring how much water can flow down the slides at once. The more inviting the ride (higher admittance), the easier it is for water (electric current) to flow. Summing the ease of each slide gives you a total flow for the park.
Resonance Conditions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Resonant Frequency (same as series):
\[ ω_0 = \frac{1}{\sqrt{LC}} \]
- Quality Factor:
\[ Q = R\sqrt{\frac{C}{L}} \]
Detailed Explanation
The resonant frequency (ω₀) of a Parallel RLC circuit is determined by the values of the inductor (L) and capacitor (C). At this frequency, the circuit tends to oscillate with maximum amplitude because the inductive and capacitive reactances cancel each other out. The Quality Factor (Q) quantifies the sharpness of the resonance; a higher Q value indicates a narrow band of frequencies around resonance where the circuit is more efficient and reactive. This is crucial in applications such as tuning radio frequencies.
Examples & Analogies
Imagine a singer hitting a perfect note that resonates with a glass. When the frequency of the sound aligns with the natural frequency of the glass, it vibrates (resonates) more intensely. The sharper the note (higher Q factor), the more pronounced the effect. In the circuit, this is similar to how certain frequencies cause the circuit to respond more robustly.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Admittance: A measure of how easily current flows in a circuit.
-
Resonant Frequency: The frequency at which a parallel RLC circuit oscillates with maximal amplitude.
-
Quality Factor: A parameter indicating how selective a circuit is at its resonant frequency.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a parallel RLC circuit with R=100Ω, L=10mH, and C=100μF, the resonant frequency ω₀ can be calculated, demonstrating the relationship between L, C, and frequency behavior.
-
By adjusting R in a parallel RLC circuit, students can observe how the quality factor (Q) changes, affecting the circuit's selectivity and bandwidth.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In circuits where parts are together, Inductors and capacitors dance like a feather. To define their role, you must understand - the resonant frequency is carefully planned.
📖 Fascinating Stories
-
Once in a land of circuits, a wise engineer created a parallel RLC circuit. The resistor insisted it was important, the inductor and capacitor argued about frequency. They soon realized that together, they created a harmonious resonance, balancing currents like friends sharing a pie!
🧠 Other Memory Gems
-
RC, LC, RL - Remember the sequence of relationships in parallel circuits with the song: 'Resistors Calm, Inductors Calm, Resonating Low!'
🎯 Super Acronyms
Remember 'RLC' for Resonant, Limited, Controlled; the ideal aspects of parallel circuits!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Admittance
Definition:
A measure of how easily a circuit allows current to flow; the reciprocal of impedance.
-
Term: Resonant Frequency (ω₀)
Definition:
The frequency at which a system naturally oscillates with greater amplitude, equal to $$1/\sqrt{LC}$$ in RLC circuits.
-
Term: Quality Factor (Q)
Definition:
A dimensionless parameter that describes how underdamped an oscillator or resonator is, indicating selectivity and bandwidth.

