Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.

Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.

Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Bandstop Filters
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Today we're going to learn about how parallel RLC circuits can be used as bandstop filters. Does anyone know what a bandstop filter is?

Isn't it a circuit that blocks certain frequencies but allows others to pass?

Exactly! And in a parallel RLC circuit, we can achieve this by controlling the input impedance. The formula for input impedance is essential for understanding how this filter works.

Can you explain the formula?

Of course! The input impedance is given by: \[ Z_{in} = \frac{R}{1 + jR(ωC - \frac{1}{ωL})} \]. This tells us how the circuit behaves at different frequencies.
Understanding Impedance in Bandstop Filters
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Let's break down the input impedance formula further. The term \( jR(ωC - \frac{1}{ωL}) \) represents the reactive part that affects how the circuit responds to different frequencies.

So, if both terms equal zero, does that mean we have maximum impedance?

Correct! When \( ωC = \frac{1}{ωL} \), we reach resonance where the impedance peaks, effectively creating a bandstop behavior.

Does this mean we can adjust R, L, or C to change the frequencies affected?

Yes! By manipulating R, L, and C, we can design filters that are tailored to specific applications.
Applications of Parallel RLC Bandstop Filters
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Can anyone think of practical applications for bandstop filters?

They could be used in audio systems to block unwanted noise frequencies!

Exactly! They're also used in communication systems to eliminate certain frequency bands that may interfere with signals.

I read about them in RF applications too. They were used to prevent interference.

Right! Bandstop filters are essential in tuning circuits to focus on desired frequencies without unwanted noise.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section describes how a parallel RLC circuit functions as a bandstop filter, emphasizing the unique input impedance characteristics that allow for specific frequencies to be attenuated while passing all others. It can help understand the practical applications of such circuits in filtering unwanted signals.
Detailed
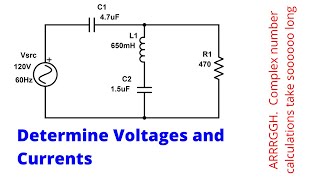
In this section, we explore the concept of a Parallel RLC circuit acting as a bandstop filter. This circuit configuration is vital for applications requiring the attenuation of specific frequency ranges while allowing other frequencies to pass. The input impedance of a parallel RLC circuit can be expressed as:
\[ Z_{in} = \frac{R}{1 + jR(ωC - \frac{1}{ωL})} \]
This formula indicates how the real component (resistance) interacts with the reactive components (inductance and capacitance) to determine the overall impedance at various frequencies. Understanding this relationship is crucial in designing circuits for signal processing and communication systems, where specific frequency bands need to be filtered out.
Youtube Videos



Audio Book
Dive deep into the subject with an immersive audiobook experience.
Input Impedance of a Parallel RLC Circuit
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The input impedance is given by the formula:
\[ Z_{in} = \frac{R}{1 + jR(ωC - \frac{1}{ωL})} \]
Detailed Explanation
The input impedance \(Z_{in}\) of a parallel RLC circuit is a complex quantity that describes how the circuit reacts to an input signal. The formula includes resistance (R), the angular frequency (ω), the capacitance (C), and the inductance (L). The presence of the imaginary unit (j) indicates that the impedance has both real (resistive) and imaginary (reactive) components. In simpler terms, it tells us how much voltage will be needed across the circuit based on its configuration at different frequencies.
Examples & Analogies
Think of a parallel RLC circuit like a busy intersection with cars (electrical current) trying to enter it. The resistance \(R\) represents the size of the road (how much traffic can pass), while the reactance components (due to 'j' terms) represent the effects of stop signs and traffic lights at different frequencies. When the intersection is 'tuned' just right, it can either stop or allow certain cars (signals) past depending on the exact conditions (frequency).
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Bandstop Filter: A type of filter that reduces the amplitude of specific frequency ranges.
-
Input Impedance: A measure of how much the parallel RLC circuit resists the input signal at various frequencies.
-
Resonance: Occurs when reactive parts negate frequency impacts, optimizing impedance.
-
RLC Configuration: The arrangement of resistors, inductors, and capacitors in a circuit determining its filtering characteristics.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
If you want to block a radio frequency of 100 MHz while allowing other frequencies through, a parallel RLC bandstop filter can be tuned to that frequency by adjusting L and C.
-
In audio equipment, a parallel RLC circuit can be used to suppress hum at 60 Hz while allowing music frequencies to pass, enhancing sound clarity.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a filter's dance, frequencies prance, / Block the unwanted, give others a chance.
📖 Fascinating Stories
-
Imagine a crowded room where a bandstop filter is the bouncer. Only specific unruly frequencies are shown the door, while harmonious sounds flow freely.
🧠 Other Memory Gems
-
RLC = Remember: L pushes back, C lets go, R sets the pace — adjust to control the show!
🎯 Super Acronyms
BANDSTOP = Banning All Noisy Disruptions, Smoothing Transmission of Ordinary Passes.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Bandstop Filter
Definition:
A filter that attenuates specific frequency ranges while allowing others to pass.
-
Term: Input Impedance
Definition:
The total impedance that a circuit presents to an incoming signal, affecting how the circuit filters frequencies.
-
Term: Resonance
Definition:
A condition where the reactive components of a circuit balance out, leading to maximum impedance.
-
Term: Reactive Components
Definition:
Components in a circuit that oppose changes in current or voltage (e.g., inductors and capacitors).

