Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.

Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.

Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Differential Equation of Series RLC Circuits
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Today, we're going to explore how a series RLC circuit reacts to changes over time. The behavior of the circuit can be described by this differential equation: L(di²/dt²) + R(di/dt) + (1/C)i = dv/dt. Can anyone identify the components involved?

It looks like we have the inductor, the resistor, and the capacitor in the equation?

Exactly! Each component introduces distinct behaviors. The inductor stores energy in a magnetic field, the capacitor stores energy in an electric field, and the resistor dissipates energy. Now, understanding this equation helps us classify the circuit responses into overdamped, critically damped, and underdamped. Can someone tell me what these terms mean?

I think overdamped means the system returns to equilibrium without oscillating, right?

Spot on, Student_2! Overdamped systems return to equilibrium more slowly compared to critically or underdamped systems. Now, can anyone think of examples where you might want an overdamped system?

Maybe in door closers? They need to shut slowly without slamming.

That's a great example! Let's summarize: The differential equation provides the foundation for analyzing the circuit's response over time.
Understanding Damping Ratios
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Now, let’s focus on the damping ratio, \(\zeta\). It's crucial for determining if the circuit is overdamped, critically damped, or underdamped. For a series RLC, the formula is \(\zeta = \frac{R}{2} \sqrt{\frac{C}{L}}\). What do you think each variable represents?

R is resistance, C is capacitance, and L is inductance. But how does this affect the performance?

Great question! The damping ratio indicates how quickly the system returns to equilibrium after a disturbance. For example, a higher damping ratio means a quicker return. What would happen if R were very small?

Then it would be underdamped, leading to oscillations before settling!

Correct! An underdamped system will oscillate, while an overdamped system won't. Let’s quickly summarize: the damping ratio is essential for predicting circuit behavior!
Comparison of Damping in RLC Circuits
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

We've focused on series RLC circuits; now let’s briefly discuss parallel configurations and how damping works there. The formula changes to \(\zeta = \frac{1}{2R}\sqrt{\frac{L}{C}}\). How do you think this affects performance compared to the series circuit?

I guess it means the resistance affects it differently compared to series?

Exactly! In parallel circuits, resistance directly influences how energy is dissipated. In what situations would you prefer a parallel over a series circuit?

Maybe in audio electronics? I think they can better manage power distribution.

Very insightful! Summarizing today, we’ve discussed differential equations and their role in determining the nature of circuit responses based on the damping ratio in both series and parallel configurations.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the time domain response of series RLC circuits, including the relevant differential equations. The key classifications of circuit responses – overdamped, critically damped, and underdamped – are introduced alongside the damping ratio concept, providing insight into how these circuits react over time.
Detailed
Time Domain Response
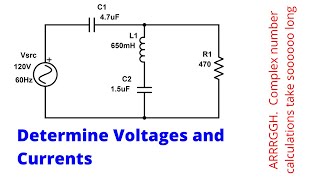
In the study of RLC circuits, the time domain response is crucial to understanding how the circuit reacts to changes over time. The section presents the differential equation governing the current in a series RLC circuit:
$$L\frac{d^2i}{dt^2} + R\frac{di}{dt} + \frac{1}{C}i = \frac{dv}{dt}$$
This equation illustrates the relationship between the inductor (L), resistor (R), and capacitor (C) in response to a varying voltage source.
Differential Equation Form
The differential equation is vital for analyzing circuit behavior, as it allows us to categorize responses based on the damping ratio \( \zeta \):
- Overdamped (\(\zeta > 1\))
- Critically damped (\(\zeta = 1\))
- Underdamped (\(\zeta < 1\))
These classifications help predict how quickly the circuit will settle to a steady state after a disturbance. The damping ratio is defined as:
-
For series RLC:
$$\zeta = \frac{R}{2} \sqrt{\frac{C}{L}}$$ -
For parallel RLC:
$$\zeta = \frac{1}{2R}\sqrt{\frac{L}{C}}$$
Importance
Understanding the time domain response of RLC circuits is essential in various applications, including filter design and circuit tuning. It provides insights into energy dissipation, oscillation damping, and system stability.
Youtube Videos



Audio Book
Dive deep into the subject with an immersive audiobook experience.
Differential Equation Form
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
2.4.1 Differential Equation Form
- Series RLC:
$$
L\frac{d^2i}{dt^2} + R\frac{di}{dt} + \frac{1}{C}i = \frac{dv}{dt}
$$ - Solutions:
- Overdamped (ζ > 1)
- Critically damped (ζ = 1)
- Underdamped (ζ < 1)
Detailed Explanation
In this section, we focus on the differential equation that describes the behavior of series RLC circuits. The equation states that a combination of inductance (L), resistance (R), and capacitance (C) influences the current (i) over time based on how quickly the voltage (v) changes. The equation has three solutions based on the damping ratio (ζ), which tells us how the circuit will respond over time:
- Overdamped (ζ > 1): The current changes slowly and does not oscillate.
- Critically damped (ζ = 1): The current changes quickly and smoothly, reaching its final value without oscillating.
- Underdamped (ζ < 1): The current changes with oscillations that gradually damp out.
These behaviors are critical to understanding how circuits react to changes in voltage and current, especially in real-world applications where quick responses are often necessary.
Examples & Analogies
You can think of the different damping effects like a swing. If the swing has too much friction (overdamped), it will return to rest slowly without going back and forth. If it has just the right amount of push (critically damped), it will come to rest quickly without swinging too far. If it’s lightly pushed (underdamped), it will go back and forth a few times before settling down.
Damping Ratio
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
2.4.2 Damping Ratio
$$
ζ = \frac{R}{2}\sqrt{\frac{C}{L}} \quad\text{(series)}
$$
$$
ζ = \frac{1}{2R}\sqrt{\frac{L}{C}} \quad\text{(parallel)}
$$
Detailed Explanation
The damping ratio (ζ) quantifies how oscillations in a circuit decay after a disturbance. For series RLC circuits, the formula shows that ζ depends on the resistance (R), inductance (L), and capacitance (C). A higher resistance leads to a higher damping ratio, indicating quicker stabilization without oscillation. Conversely, the formula for parallel RLC circuits shows how they behave in a similar way but with different dependencies. Understanding the damping ratio helps engineers design circuits that behave predictably under changes.
Examples & Analogies
Imagine a car's suspension system. A well-tuned suspension responds quickly to bumps (critically damped), while a suspension system that is too stiff would be uncomfortable (overdamped), responding too slowly to bumps. A suspension that's too soft allows the car to bounce around (underdamped). Just like a well-tuned suspension, a circuit needs the right level of damping for optimal performance.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Differential Equation: The equation governing the current in the RLC circuit describes its time domain response.
-
Damping Ratio: A key parameter that describes whether the response is overdamped, critically damped, or underdamped.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An example of an overdamped circuit is a slow-closing door; it doesn’t slam but takes time to settle.
-
A car suspension system can be designed to be underdamped for better comfort when driving over bumpy roads.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Under, Over, Critical too, damping helps know what circuits do!
📖 Fascinating Stories
-
Imagine a bouncy ball (underdamped) that swings back and forth after flicking it, while a door (overdamped) closed slowly without slamming.
🧠 Other Memory Gems
-
Remember: 'C U O' for Critical, Under, Over – it helps recall the types of damping!
🎯 Super Acronyms
DAMP
- Damping
- Analyze
- Measure
- Predict – the process to understand circuit responses.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Damping Ratio
Definition:
A dimensionless measure describing how oscillations in a system decay after a disturbance.
-
Term: Overdamped
Definition:
A condition where the damping ratio is greater than one, leading to a gradual return to equilibrium without oscillations.
-
Term: Critically damped
Definition:
A condition where the system returns to equilibrium as quickly as possible without oscillating.
-
Term: Underdamped
Definition:
A condition where the damping ratio is less than one, resulting in oscillations as the system returns to equilibrium.

