Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Frequency Response and Transfer Functions
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, weβre going to explore the frequency response of amplifiers. What do we mean by 'frequency response', and why is it important?
Is it how the amplifier behaves at different frequencies?
Exactly! The frequency response shows how the amplifierβs gain varies with frequency. We often express this using transfer functions. Can anyone tell me what the transfer function is?
Is it the ratio of output to input in the frequency domain?
Correct! It tells us how input signals are transformed at different frequencies. We convert the circuit in the Laplace domain to find these functions.
How do we go from the Laplace domain to the Fourier domain?
We substitute 's' with 'jΟ' for frequency analysis. This aids in generating gain and phase plots.
Whatβs the significance of those plots?
They visually represent how the output changes over frequency, which is key for understanding amplifier performance.
In summary, the transfer function is crucial in decoding amplifier behavior, linking input frequency to output. Let's remember this with the acronym 'GAIN' - Gain Analysis Indicates Frequency response.
Corner Frequency and Gain Roll-Off
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Letβs discuss corner frequencies and their role in amplifier gain. Who can tell us what happens at the corner frequency?
That's when the gain starts to drop, right?
Yes! Specifically, the gain starts to roll off at -20 dB per decade. Why do you think that happens?
Maybe because the impedance of capacitors changes at higher frequencies?
Spot on! At corner frequencies, capacitors begin to dominate, reducing gain. To visualize this, we plot a Bode plot, where we can see the linear behavior before rolling off.
So is the corner frequency related to the pole location in the Laplace domain?
Exactly! The pole's location determines the corner frequency. A pole closer to the imaginary axis usually indicates a lower corner frequency. Keep this linkage in mindβitβs key for circuit design!
To remember this, letβs use the mnemonic 'CUP' - Corner frequency Under Pole location.
Phase Response
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we will talk about phase response in amplifiers. What does phase response indicate?
Is it the shift in the output signal compared to the input?
Yes! The phase response shows how much time delay there is between input and output. At low frequency, we can expect phase shifts to be 0 degrees.
What happens as we approach the corner frequency?
Great question! As we approach the corner frequency, the phase shifts towards -45 degrees. Beyond it, the phase approaches -90 degrees.
That's a significant change!
Indeed! Itβs vital when synchronizing multiple circuit elements. Remember: 'PHASE' - Phase Harmonization Affects Signal Elements.
In summary: phase response is crucial for designing systems where timing is essential, ensuring signals arrive at the right moments.
Bode Plot Analysis
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now letβs delve into Bode plots. Who can explain what a Bode plot represents?
Isnβt it a graphical representation of gain and phase versus frequency on logarithmic scales?
Exactly right! Bode plots leverage the logarithmic scale to better display amplifier behavior, especially over wide frequency ranges.
How do we determine corner frequencies from these plots?
The corner frequency is typically identified where the gain crosses -3 dB. This point marks the boundary between passband and roll-off region.
Can we utilize Bode plots for both low-pass and high-pass filters?
Absolutely! Bode plots apply to both types, allowing engineers to visually analyze circuits. To remember this, think 'LINES' - Logarithmic Illustration for Network Evaluations and Signals.
In summary, Bode plots are instrumental in understanding overall amplifier performance and making design decisions.
Practical Applications of Frequency Response
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Letβs tie our concepts together. How can understanding frequency response affect amplifier design?
It helps optimize the circuit for the intended frequency range!
Correct! Optimizing circuits is vital, especially in audio or radio frequency applications, ensuring clarity and fidelity in signals.
What if we miscalculate the corner frequency?
That could lead to distortion or unwanted filtering! Thus, careful analysis is necessary during design. Remember: use tools like simulation software for accurate modeling.
Whatβs the biggest takeaway for our designs?
Understanding the interplay of gain, frequency response, and phase shift is crucial for designing effective amplifiers. Think of the acronym 'DESIGN' - Dynamic Evaluations of Signal Gain Needs.
In conclusion, our grasp of frequency response shapes better amplifier designs, ensuring they meet performance standards.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the concepts of frequency response in CE and CS amplifiers are explored, focusing on transfer functions in the Laplace and Fourier domains. The section highlights gain and phase plots, corner frequency determination, and the relationship between poles in Laplace analysis and frequency response.
Detailed
In-Depth Summary
This section delves into the frequency response characteristics of CE and CS amplifiers, emphasizing the analysis of R-C circuits through the Laplace domain. By transforming circuit elements into the Laplace domain, we establish transfer functions that express the relationship between input and output signals.
The frequency response is essential for understanding how amplifiers behave across varying frequencies. The section explains how to switch from the Laplace domain to the Fourier domain by substituting \'s\' with \'jΟ\', allowing for the construction of gain and phase plots. The significance of corner frequencies is also discussed; here, the gain magnitude generally remains constant until reaching a specific corner frequency, at which point it begins to roll off at a rate of -20 dB per decade.
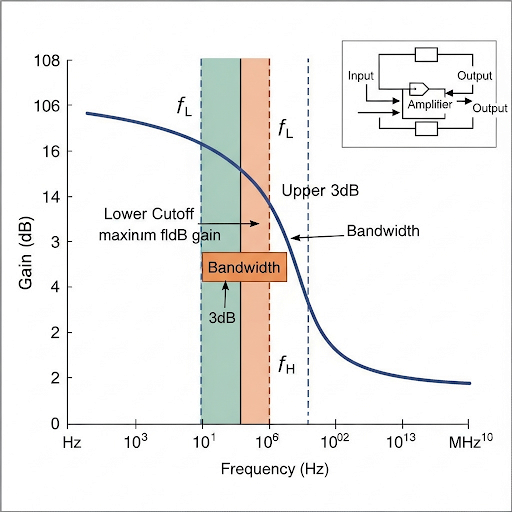
Critical analysis of poles within the transfer functions determines cut-off frequencies, making it possible to ascertain the behavior and performance of the amplifier in practical scenarios. The narrative also includes the interaction between R-C elements, the implications of loading effects when cascading circuits, and the concept of Bode plots for extensive frequency analysis. Understanding these parameters is crucial for designing effective amplifiers with predictable behaviors.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Frequency Response Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, welcome back to this R-C circuit frequency response after the short break.
(Refer Slide Time: 00:31)
So, similar to the C-R circuit again here what you are doing is that we are taking the circuit into Laplace domain...
Detailed Explanation
In this chunk, the speaker introduces the concept of analyzing frequency response using an R-C circuit in the Laplace domain. The approach involves transforming the circuit elements into their impedance equivalents to facilitate mathematical analysis. The use of Laplace transforms allows for easier manipulation of circuits by simplifying differential equations to algebraic ones, making it easier to understand how the circuit will behave at different frequencies.
Examples & Analogies
Think of taking a photo of a moving car. If the car (the circuit) is moving quickly, using a slower shutter speed (Laplace transformation) will blur the image, making it difficult to see details (frequency response). However, if you adjust the settings and use a faster speed, the photo becomes clearer, analogous to analyzing the circuitβs frequency response more accurately.
Substituting s with jΟ for Fourier Transform
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, to get the frequency response as I said for the previous case what you have to do, we have to take this replace this s by jΟ or rather I was having say sigma part in s which I am making it 0...
Detailed Explanation
This section discusses how to convert the Laplace domain analysis to the Fourier domain by substituting the Laplace variable 's' with 'jΟ', where 'j' is the imaginary unit and 'Ο' represents angular frequency. Dropping the sigma component simplifies the analysis to focus solely on the oscillatory behavior at different frequencies.
Examples & Analogies
Consider tuning a radio to different frequencies. Each FM station's frequency corresponds to a specific 'Ο'. By checking each station's clarity (the circuit's frequency response), we understand which frequencies are allowed through and which are not, similar to how we replace 's' with 'jΟ' to examine the response of our circuit.
Magnitude and Phase Response
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, again here what you can do? We can plot the magnitude. So, if we consider the | | and with respect to Ο...
Detailed Explanation
The speaker highlights the process of plotting the magnitude and phase response of the frequency response. This entails understanding how the output signal changes in magnitude and phase with respect to different input frequencies. At low frequencies, the output closely resembles the input, while at high frequencies, the impact of capacitive impedance changes how signals pass through.
Examples & Analogies
Imagine listening to a musical track through a stereo system. At low volume (low frequency), all instruments sound clear. Increasing the volume (higher frequency) may cause distortion or muffled sounds from certain instruments. Thus, different frequency components modify how music (the circuit output) is received.
Understanding the Frequency Bands
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, I can say that the circuit it is again it is having two range of frequency β one is pass band, another is the stock band...
Detailed Explanation
This section discusses how amplifier circuits have different frequency response regionsβpass band (where signals are allowed to pass) and stop band (where signals are attenuated). The transition point between these bands occurs at the corner frequency, where the reactive elements in the circuit start having significant effects on the overall impedance.
Examples & Analogies
Think of a water filter: it allows clean water (signals) to pass through while blocking dirt (unwanted frequencies). The clean water represents the pass band, and as you try to push muddy water through, the filter stops it, representing the stop band.
The Bode Plot Representation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, similar to the previous case again since we like to see the wide range of frequency and the behavior of the frequency response over wide range...
Detailed Explanation
In this part, the focus is on creating a Bode plot, a graphical representation of frequency response using logarithmic scales for frequency and decibels for gain. Bode plots facilitate the visualization of corner frequencies and the gain roll-off in a circuit, providing insights into the amplifier's performance over a wide frequency spectrum.
Examples & Analogies
Visualizing a Bode plot is like viewing a city map in a zoomed-out perspective. Certain landmarks (corner frequencies) stand out; the layout provides insights into your route options (gain variations at frequencies), helping you navigate your travel across the city (range of frequencies).
Corner Frequency and Cutoff Relationships
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, here again we are getting a direct relationship of this pole and this corner frequency...
Detailed Explanation
This section explains the relationship between the pole of the transfer function in the Laplace domain and the cutoff frequency in the frequency response. The location of the pole determines where the circuit starts to attenuate the signal, marking the critical point in the behavior of the amplifier.
Examples & Analogies
Imagine a hill's gradient. The peak point is akin to the pole, influencing how steeply you ascend (gain) before reaching the top (cutoff frequency). If you continue past a certain point, the hill declines (signal attenuation) rapidly.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Frequency Response: Indicates how amplifiers respond to different frequencies.
-
Transfer Functions: A mathematical tool for analyzing amplifier behavior.
-
Corner Frequency: The point where gain starts to decrease.
-
Bode Plots: Essential for visualizing gain and phase across frequencies.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An audio amplifier that attenuates frequencies beyond 20 kHz, showing its low-pass frequency response.
-
A common source amplifier with a corner frequency at 1 kHz, indicating its effective operation range.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
For gain and phase, keep in mind, the corner shows where losses youβll find.
π Fascinating Stories
-
Imagine an amplifier at a concert, pumping sound until certain frequencies begin to crackle; thatβs where its corner frequency gets in the way.
π§ Other Memory Gems
-
Remember 'GAP' - Gain Analysis of Poles; it highlights how pole locations impact frequency response.
π― Super Acronyms
CUP - Corner frequency Under Pole location; relates poles to their impact on amplifier behavior.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Frequency Response
Definition:
The measure of an amplifier's output signal relative to its input signal across various frequencies.
-
Term: Transfer Function
Definition:
A mathematical representation that expresses the relationship between the input and output of a system in the frequency domain.
-
Term: Corner Frequency
Definition:
The frequency at which a filter's response begins to roll off, typically defined at -3 dB on a gain plot.
-
Term: Bode Plot
Definition:
A graphical representation of a system's frequency response, plotting gain and phase against frequency on a logarithmic scale.
-
Term: Pole
Definition:
A frequency at which the gain of a system approaches infinity in the context of its transfer function.
-
Term: Gain RollOff
Definition:
The decrease in gain experienced by a system at frequencies above its corner frequency.
-
Term: Phase Shift
Definition:
The difference in phase between the input and output signals, expressed in degrees.
-
Term: Impedance
Definition:
The total opposition a circuit presents to the flow of alternating current, influenced by resistance and reactance.