Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Vector Equality
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we'll learn about the equality of vectors. What do we think makes two vectors equal?
I think they need to be the same length.
That's correct! But there's more. Can anyone tell me what else matters?
They also need to have the same direction!
Exactly! So, two vectors are only equal if they have the same magnitude and direction. A quick way to remember this is: "Magnitude and Direction, that's the connection!"
Verifying Vector Equality
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now letβs explore how to verify if two vectors are equal. Can anyone explain how we might do that?
We could draw them out and see if they match up!
Great idea! We can shift one vector parallel to itself and see if it matches the other. What do we call this method?
Itβs the graphical method of verifying vector equality!
Spot on! Remember, if their tails and tips coincide after adjusting, they are equal. This visualization reinforces our understanding of vector operations.
Examples of Equal and Unequal Vectors
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Letβs identify some vectors. If vector A has a magnitude of 5 units upwards, what about vector B, which has a magnitude of 5 units but points downwards?
They have the same length, but they point in opposite directions, so they are not equal.
Correct! Even though they are the same size, their direction matters. Remember, equal vectors can't just look the same; they must also point the same way!
So, if one is inverted, they are definitely not equal.
Exactly! This reinforces the idea that direction is key in vector analysis.
Practical Implications of Vector Equality
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Understanding vector equality helps in many real-world applications, especially in physics. Why do you think this knowledge is helpful?
It helps when adding forces or velocities, right?
Exactly! Vector equality allows us to properly manipulate and add vectors in physics problems, ensuring accurate results. Remember, when in doubt, consider both magnitude and direction!
It's like using a compass! If your directions donβt match, you could end up lost.
That's a great analogy! Itβs all about precision and understanding.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Equality of vectors is determined by both magnitude and direction. The section explains how to verify vector equality and distinguishes between equal and unequal vectors.
Detailed
Equality of Vectors
In this section, we discuss the concept of vector equality. Two vectors, A and B, are said to be equal if and only if they possess the same magnitude and direction. This characteristic is important because it establishes the foundational understanding of how vectors can be compared and manipulated.
To verify if two vectors are equal, we can visualize them. For any two vectors A and B, if we can place one vector on top of the other such that both their tails and tips coincide, they are considered equal. This can be demonstrated effectively using graphical methods, such as shifting vector B parallel to itself until its tail aligns with that of vector A. If the tips of vectors A and B also coincide post the adjustment, A is equal to B (A = B).
On the contrary, if two vectors have the same magnitude but different directions, such as A' and B', they are not equal. Even shifting vector B' parallel will not allow it to coincide with vector A. Thus, understanding the equality of vectors is critical as it assists in visualizing vector addition, subtraction, and resolving complex vector equations in physics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Equality of Vectors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Two vectors A and B are said to be equal if, and only if, they have the same magnitude and the same direction.
Detailed Explanation
In vector mathematics, two vectors can be considered equal if they are identical in both length and direction. This means that if vector A points north with a length of 5 units, and another vector B also points north with the same length of 5 units, then A = B. This equality condition is critical in physics as it allows us to replace one vector with another in calculations without changing the result.
Examples & Analogies
Imagine two cars that drive along the exact same road at the same speed and direction. Even if they start from different points, as long as they maintain speed and direction the same, they can be considered equal in terms of their velocity vectors.
Visualizing Vector Equality
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
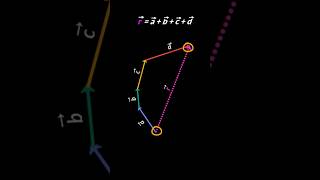
Figure 3.2(a) shows two equal vectors A and B. We can easily check their equality. Shift B parallel to itself until its tail Q coincides with that of A, i.e., Q coincides with O. Then, since their tips S and P also coincide, the two vectors are said to be equal.
Detailed Explanation
To confirm that two vectors are equal, you can visualize moving one vector so that it perfectly overlaps with the other. In Figure 3.2(a), if vector B can be shifted along its own line to match the tail of vector A at point O, and if both vectors' heads meet at the same point, it proves that they are equal. This shifting process illustrates the concept that vectors are not tied to a specific position but rather to their magnitude and direction.
Examples & Analogies
Think of arrows being placed in a target. If you can move one arrow right on top of another without changing its direction or length, it exemplifies the equality of vectors. The arrows represent vectors, and if they match in both aspects, they are equal.
Magnitude and Direction
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In general, equality is indicated as A = B. Note that in Fig. 3.2(b), vectors Aβ² and Bβ² have the same magnitude but they are not equal because they have different directions.
Detailed Explanation
The notation A = B indicates that vectors A and B are equal regarding both their magnitude and direction. However, if two vectors have the same magnitude but point in different directions, they are not considered equal. For example, two vectors of 5 units in length, one pointing east and the other pointing west, highlight that magnitudes alone do not define equality; direction also plays a critical role.
Examples & Analogies
If two people are walking the same distance of 100 meters, yet one walks south and the other walks north, despite covering the same physical distance (magnitude), they are not moving in the same direction and therefore represent different vectors.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Equality of Vectors: Vectors are equal if they have both the same magnitude and direction.
-
Graphical Representation: Equal vectors can overlap perfectly when placed vectorially on top of each other.
-
Distinction: Vectors with equal magnitudes but different directions cannot be considered equal.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: If vector A points 5 units up, and vector B points 5 units down, these vectors are not equal due to their opposite directions.
-
Example 2: Vector A and Vector B are both 3 units to the right; they are equal since they have the same magnitude and direction.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
Vectors equal, to measure and check, in both length and direction, you get the perfect spec.
π Fascinating Stories
-
Imagine two brothers, one moving north and the other south β though they look alike, they arenβt equal as they take a different route.
π§ Other Memory Gems
-
M&D for Magnitude and Direction - remember this for vector connection!
π― Super Acronyms
E&D
- Equality & Direction to remember the qualities of equal vectors.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Vector
Definition:
A quantity defined by both magnitude and direction.
-
Term: Magnitude
Definition:
The size or length of a vector, measuring its strength.
-
Term: Direction
Definition:
The orientation of a vector in space.
-
Term: Graphical Method
Definition:
A way to visually verify vector equality by adjusting their position.