Learn
Games

3.6.1 - Position Vector and Displacement

Interactive Audio Lesson

Listen to a student-teacher conversation explaining the topic in a relatable way.

Understanding Position Vectors

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Today we're going to explore the concept of the position vector. In a two-dimensional plane, we express the position of a particle using its coordinates along the x and y axes. Can anyone tell me the basic form of a position vector?

Student 1
Student 1

Is it r = x i + y j?

Teacher
Teacher

That's correct! The position vector r can indeed be written as r = x i + y j, where x and y are the coordinates of the particle. This helps us pinpoint exactly where the particle is in the plane.

Student 3
Student 3

Why do we use i and j?

Teacher
Teacher

Great question! The 'i' and 'j' represent unit vectors in the direction of the x and y axes respectively. They help convey the direction of these coordinates.

Teacher
Teacher

To remember this, think of 'I' as pointing straight right and 'J' as pointing straight up. So when we use them together, we're indicating a location on the entire plane!

Student 2
Student 2

I see! Can we work through a simple position vector example?

Teacher
Teacher

Absolutely! Let's say we have a particle at coordinates (3, 4). What would its position vector be?

Student 4
Student 4

It would be r = 3i + 4j!

Teacher
Teacher

Correct! Now let’s summarize: The position vector helps us locate a particle by representing its coordinates and direction using i and j.

Exploring Displacement

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Now that we understand position vectors, let's talk about displacement. Can anyone explain what displacement means?

Student 1
Student 1

Is it the distance moved by the particle from one position to another?

Teacher
Teacher

Yes, but it's more than just distance! Displacement is a vector quantity that has both magnitude and direction. It is defined as the difference between the initial and final position vectors.

Student 3
Student 3

So how do we calculate it?

Teacher
Teacher

We use the equation ∆r = r' - r. If r' is the position vector at time t′ and r is at time t, the displacement can be written as ∆r = (x' - x)i + (y' - y)j.

Student 2
Student 2

What do ∆x and ∆y represent in this equation?

Teacher
Teacher

Good catch! ∆x is the change in the x-coordinate, and ∆y is the change in the y-coordinate during the movement from point P to point P′.

Teacher
Teacher

To recap, displacement represents how far and in what direction the particle moves from its initial to final position, and we calculate it using the difference in position vectors!

Components of Displacement

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Let's take a closer look at the component form of displacement. When calculating it, we break it down into its x and y components.

Student 1
Student 1

Can you remind us what those components are?

Teacher
Teacher

Certainly! The components are ∆x = x' - x for the x-direction and ∆y = y' - y for the y-direction.

Student 4
Student 4

So if I move from (2, 3) to (5, 7), what would my displacement be?

Teacher
Teacher

Excellent question! First, we find ∆x and ∆y. Here, ∆x = 5 - 2 = 3 and ∆y = 7 - 3 = 4. Thus, the displacement vector is ∆r = 3i + 4j.

Student 2
Student 2

And that means I have moved 3 units in the x direction and 4 units in the y direction?

Teacher
Teacher

Exactly! By understanding the components, you can visualize and calculate movements within this two-dimensional space. Remember: direction matters!

Teacher
Teacher

To sum it up: displacement is calculated using the differences in the position components, allowing us to grasp not only how far a particle has traveled but also in which direction.

Introduction & Overview

Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.

Quick Overview

This section introduces the concept of the position vector and how displacement is calculated using the position of a particle in a two-dimensional plane.

Standard

The section explains the position vector, denoted as r, representing a particle's location in an x-y coordinate system. It also defines displacement as the difference between the initial and final position vectors, introducing key equations that illustrate these concepts and their mathematical representations.

Detailed

Position Vector and Displacement

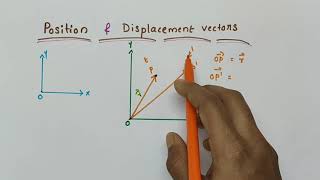
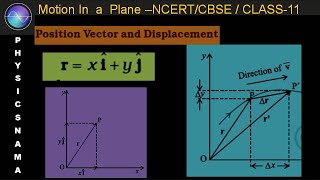
The position vector r of a particle P in a two-dimensional plane is represented by the equation:

r = x i + y j

where x and y denote the particle's coordinates along the x-axis and y-axis respectively, and i and j are the unit vectors in the direction of the x and y axes. The concept of the position vector helps in determining the location of a particle relative to a fixed point, typically the origin of a coordinate system.

Moreover, the section discusses how to calculate displacement (∆r), which is defined as the difference between the position vectors at two different times, t and t′. The formula is given as:

∆r = r' - r

This can be expressed component-wise:

∆r = (x' - x)i + (y' - y)j

where ∆x = x' - x and ∆y = y’ - y.

Understanding these concepts is crucial as they form the foundation for analyzing motion, velocity, and other kinematic quantities in physics.

Youtube Videos

Position and Displacement Vector in a Plane - Motion in a Plane | Class 11 Physics
Position and Displacement Vector in a Plane - Motion in a Plane | Class 11 Physics
Motion in a plane: position vector and displacement // Class 11 Physics /Chapter 4 Motion in a plane
Motion in a plane: position vector and displacement // Class 11 Physics /Chapter 4 Motion in a plane
Position vectors and displacement vectors // Class 11 Physics // Chapter 4 - Motion in a plane
Position vectors and displacement vectors // Class 11 Physics // Chapter 4 - Motion in a plane
POSITION VECTOR AND DISPLACEMENT VECTOR|CHAPTER 3| MOTION IN A PLANE| NCERT | NEET
POSITION VECTOR AND DISPLACEMENT VECTOR|CHAPTER 3| MOTION IN A PLANE| NCERT | NEET
Position Vector | Displacement Vector | Chapter 3 | Motion in a Plane | Class 11 Physics
Position Vector | Displacement Vector | Chapter 3 | Motion in a Plane | Class 11 Physics
Position Vector and Displacement-Motion in a Plane- -Class-11 Physics CBSE NCERT IIT NEET
Position Vector and Displacement-Motion in a Plane- -Class-11 Physics CBSE NCERT IIT NEET
Vectors 08 : Position Vector and Displacement Vector with FEEL || Best Questions || JEE /NEET
Vectors 08 : Position Vector and Displacement Vector with FEEL || Best Questions || JEE /NEET
🤔🤔position and displacement vectors class 11|| lec 3
🤔🤔position and displacement vectors class 11|| lec 3
Motion in a Plane | Class 11 Physics | Chapter 4 | 4.2.1 Position and Displacement Vectors
Motion in a Plane | Class 11 Physics | Chapter 4 | 4.2.1 Position and Displacement Vectors
L#5 | Class 11 | Motion in a plane (position vector & displacement vector)
L#5 | Class 11 | Motion in a plane (position vector & displacement vector)

Audio Book

Dive deep into the subject with an immersive audiobook experience.

Position Vector

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

The position vector r of a particle P located in a plane with reference to the origin of an x-y reference frame is given by r = x ɵi + y ɵj, where x and y are components of r along x- and y- axes or simply they are the coordinates of the object.

Detailed Explanation

The position vector, r, represents the location of a particle P in a two-dimensional plane. This vector is expressed in terms of its components along the x-axis (x) and y-axis (y). By using unit vectors ɵi and ɵj, which point in the positive x and y directions respectively, we can write r as r = x ɵi + y ɵj. Here, x is the horizontal coordinate, while y is the vertical coordinate, giving us a full description of the position of the particle relative to the origin (0,0) of the coordinate system.

Examples & Analogies

Think about locating a point on a map: the x-coordinate could represent how far east you are from a certain reference point, while the y-coordinate might represent how far north you are. For instance, if a building is located 3 units east and 4 units north of your starting position, you could describe its location with the position vector r = 3 ɵi + 4 ɵj.

Displacement

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

Suppose a particle moves along the curve shown by the thick line and is at P at time t and P′ at time t′. Then, the displacement is: ∆r = r′ – r and is directed from P to P′.

Detailed Explanation

Displacement is a vector quantity that describes the change in position of a particle from an initial point P at time t to a final point P′ at time t′. It is given by the equation ∆r = r′ – r, meaning that we subtract the initial position vector r from the final position vector r′. The result, ∆r, indicates not only how far the particle has moved but also in which direction it has moved from P to P′.

Examples & Analogies

Imagine you walk from your home (point P) to a friend's house (point P′). The distance you walked is not the same as the displacement. Even if you walked a long path around the neighborhood, the displacement would simply be the straight-line distance from your home to your friend's house, indicating how far away you are now from your starting point, regardless of the path taken.

Displacement Components

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

We can write Eq. (3.25) in a component form: ∆r = (x' - x) ɵi + (y' - y) ɵj.

Detailed Explanation

In component form, the displacement vector ∆r can be expressed in terms of the changes in the x and y coordinates. Here, ∆x = x′ - x and ∆y = y′ - y represent the differences in each coordinate. Therefore, the displacement vector is written as ∆r = ∆x ɵi + ∆y ɵj, which clearly shows how much the position changes in both the x and y directions, combining them into a single displacement vector.

Examples & Analogies

Returning to the earlier example of walking to a friend's house, if your home is at (1, 2) and your friend's house is at (4, 6), the change in position or displacement would be (4 - 1) in the x-direction (3 units) and (6 - 2) in the y-direction (4 units). Thus, we could express your total displacement towards your friend’s house as (3 ɵi + 4 ɵj).

Average Velocity

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

The average velocity (v) of an object is the ratio of the displacement and the corresponding time interval: v = ∆r / ∆t.

Detailed Explanation

Average velocity is defined as the displacement of an object divided by the time taken to achieve that displacement. The formula v = ∆r / ∆t shows how average velocity not only depends on how much distance is covered but also the time taken to cover it. A larger displacement in a shorter time results in a higher average velocity.

Examples & Analogies

If you run 100 meters straight and it took you 10 seconds, your average velocity would be 10 meters per second (m/s). If you took 20 seconds to run the same distance, your average velocity would drop to 5 m/s, illustrating how both distance and time impact your average speed.

Instantaneous Velocity

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

The velocity (instantaneous velocity) is given by the limiting value of the average velocity as the time interval approaches zero: v = lim (∆r/∆t) as ∆t → 0.

Detailed Explanation

Instantaneous velocity represents the velocity of an object at a specific point in time. It is derived as the average velocity when the time interval approaches zero. This means looking at an object's displacement over smaller and smaller time intervals to find out exactly how fast it is moving at that very moment. The mathematical expression shows this limiting process.

Examples & Analogies

If you were to watch your friend run at a track from very close, you could see how fast they are moving at any moment. Instead of measuring their speed over a longer distance, you would eventually get a very precise reading of their speed at that exact moment. This is akin to using a speedometer in a car, which shows how fast you're currently driving, rather than the average speed over the entire trip.

Acceleration

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

The average acceleration a of an object for a time interval ∆t moving in x-y plane is the change in velocity divided by the time interval: a = ∆v / ∆t.

Detailed Explanation

Average acceleration quantifies how quickly the velocity of an object changes over a given time interval. The formula a = ∆v / ∆t indicates that the change in velocity (∆v) divided by the time taken (∆t) gives us the average acceleration. This can represent speeding up, slowing down, or changing direction, all of which are aspects of acceleration.

Examples & Analogies

If you are driving a car and you accelerate from 0 to 60 km/h in 5 seconds, your acceleration is calculated by the change in speed (60 km/h) divided by the time taken (5 seconds), which gives you a measure of how quickly you are speeding up. If it took longer, your acceleration would be less, illustrating how time is an important factor in determining acceleration.

Definitions & Key Concepts

Learn essential terms and foundational ideas that form the basis of the topic.

Key Concepts

  • Position Vector: Represents the location of a particle in space using its coordinates.

  • Displacement: Represents the change in position, accounting for direction.

  • Component Form: Breaks displacement down into changes along the x and y axes.

Examples & Real-Life Applications

See how the concepts apply in real-world scenarios to understand their practical implications.

Examples

  • For a particle at coordinates (4, 5), its position vector is r = 4i + 5j.

  • If a particle moves from (1, 2) to (5, 6), the displacement ∆r = (5 - 1)i + (6 - 2)j = 4i + 4j.

Memory Aids

Use mnemonics, acronyms, or visual cues to help remember key information more easily.

🎵 Rhymes Time

  • From point A to point B, my position you will see; with i's and j's, I’ll make it clear, displacement’s true direction is near.

📖 Fascinating Stories

  • Once upon a time in a 2D realm, a little dot named P wanted to know how far it had moved to reach P′. With its trusty position vector map, it figured out its path was indeed a displacement from where it started!

🧠 Other Memory Gems

  • Remember 'RIPE': R is for position vector, I is for i-direction, P is for the change in positions, and E is for the effect of displacement!

🎯 Super Acronyms

For displacement, think 'D = R' (Displacement equals the difference in Position vectors).

Flash Cards

Review key concepts with flashcards.

Glossary of Terms

Review the Definitions for terms.

  • Term: Position Vector

    Definition:

    A vector that specifies the position of a point or particle in a coordinate system, using coordinates along defined axes.

  • Term: Displacement

    Definition:

    A vector quantity that denotes the change in position of a particle, defined as the difference between initial and final position vectors.

  • Term: Component Form

    Definition:

    A representation of a vector in terms of its components along specified axes, such as x and y in a 2D plane.

  • Term: Unit Vector

    Definition:

    A vector of length one that indicates direction, usually denoted as i (for x direction) and j (for y direction).

  • Term: Magnitude

    Definition:

    The length of a vector, which is a scalar quantity reflecting the distance without direction.