Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Uniform Circular Motion
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we are going to learn about uniform circular motion. Can anyone explain what they think this means?
Is it when something moves around in a circle at a steady speed?
Exactly! 'Uniform' means the speed is constant, but the direction is always changing, so the velocity changes too. Why do you think this happens?
Because the path is circular? It keeps turning.
That's correct! This change in velocity leads to what's called centripetal acceleration, which is directed towards the center of the circular path. Can anyone tell me how we calculate this acceleration?
Is it something like speed squared divided by the radius?
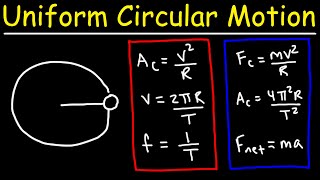
Right again! The formula is \( a_c = \frac{v^2}{R} \). Great work! Let's remember this with the acronym AC = VΒ²/R.
Centripetal Acceleration
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let's focus more on centripetal acceleration. Who can remind us what direction this acceleration points?
Towards the center of the circle!
Exactly! So what do you think would happen to the acceleration if the speed increased?
Would it get bigger because `v` is squared in the formula?
Yes! Thus, as speed increases, the centripetal acceleration increases dramatically because of that squaring effect. Letβs summarize: if speed doubles, acceleration increases by four times!
Relationship between Linear and Angular Speed
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Next, letβs discuss how we can convert between linear and angular speeds. If I say that an object moves with a linear speed \( v \), how can we express this in terms of angular speed \( \omega \)?
Is it \( v = R \omega \)?
Exactly! It connects the two concepts. So how would we find acceleration in terms of angular speed?
Wouldn't it be \( a_c = R \omega^2 \)?
Yes! Youβre all doing a fantastic job. Remember, for any uniform circular motion, we can switch between these two forms easily.
Real-Life Applications of Uniform Circular Motion
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Letβs apply our understanding to real-life scenarios. Can someone think of an example of uniform circular motion?
Like a car turning around a circular track?
Yes! Exactly. And what can we say about the forces acting on the car?
The tires provide the centripetal force that keeps the car moving in a circle.
Correct! The force is always directed towards the center. Knowing this helps us understand not just motion but safety in driving too.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In uniform circular motion, an object travels around a circular path at a constant speed, meaning the magnitude of its velocity remains constant while its direction changes continuously. This results in a centripetal acceleration directed towards the center of the circular path, quantified as the square of the speed divided by the radius of the circle.
Detailed
Detailed Summary
Uniform circular motion describes the motion of an object moving in a circular path at a constant speed. Although the object's speed remains consistent, its velocity is not constant due to a continual change in direction. This variation in velocity gives rise to a form of acceleration known as centripetal acceleration, which always acts towards the center of the circular path. The magnitude of centripetal acceleration can be calculated using the formula:
\[ a_c = \frac{v^2}{R} \]
where \( v \) is the linear speed of the object and \( R \) is the radius of the circular path. Furthermore, we can relate linear speed to angular speed, denoted by \( \omega \), with the equations:
\[ v = R \omega \]
\[ a_c = R \omega^2 \]
In uniform circular motion, the acceleration is uniform in magnitude but continuously changes in direction as it points towards the center of the circle. This section highlights the significant principles that govern uniform circular motion, including formulas for linear and angular speeds, and their implications in practical scenarios such as motion on a curved path.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Uniform Circular Motion
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When an object follows a circular path at a constant speed, the motion of the object is called uniform circular motion. The word "uniform" refers to the speed, which is uniform (constant) throughout the motion.
Detailed Explanation
Uniform circular motion occurs when an object moves in a circular path while maintaining a constant speed. Though the speed remains constant, the object's direction is continuously changing, which indicates that the object is accelerating. It is crucial to distinguish that uniform circular motion does not mean the object is moving in a straight line; rather, it means it is consistently moving at the same speed in a circular trajectory.
Examples & Analogies
Consider a Ferris wheel at an amusement park. As it revolves, the wheel's speed remains steady, but the direction of the passengers changes continuously as they move around the circle. This is a practical illustration of uniform circular motion: they move at a constant speed while their direction changes.
Acceleration in Uniform Circular Motion
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Suppose an object is moving with uniform speed v in a circle of radius R. Since the velocity of the object is changing continuously in direction, the object undergoes acceleration.
Detailed Explanation
Even though the speed is constant, there is an acceleration because the direction of the velocity vector is changing. This acceleration is directed towards the center of the circular path, known as centripetal acceleration. It is crucial to understand that acceleration in circular motion is not about speeding up or slowing down but about the change in direction.
Examples & Analogies
Think about a car driving on a circular track. While the car maintains a steady speed, its direction changes constantly as it navigates the curves. Because it continuously alters its direction, it experiences an acceleration directed inward, towards the center of the circular track.
Finding Magnitude of Centripetal Acceleration
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The centripetal acceleration ac is given by the formula ac = vΒ²/R.
Detailed Explanation
Centripetal acceleration can be calculated using the formula ac = vΒ²/R, where v is the speed of the object moving in a circle, and R is the radius of the circle. This formula shows that the acceleration is dependent on both the speed of the object and the radius of the path it follows. The faster the object is moving, or the smaller the radius, the greater the centripetal acceleration.
Examples & Analogies
Imagine a child swinging a ball on a string around in a circular motion. If the child swings the ball faster, the tension in the string increases to keep the ball moving in its circular path. This increase in speed leads to a higher centripetal acceleration, showing how speed and radius affect the force needed to maintain such motion.
Angular Speed and Relations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We define the angular speed Ο (Greek letter omega) as the time rate of change of angular displacement.
Detailed Explanation
Angular speed, denoted by Ο, measures how quickly an object rotates around a circle. It is defined as the angle (in radians) that the object covers per unit of time. A relationship exists between linear speed (v) and angular speed: v = ΟR, where R is the radius of the circular path. This indicates that as an object's angular speed increases, so does its linear speed.
Examples & Analogies
Consider a merry-go-round; the faster it spins, the quicker each horse moves around the circle. This illustrates how angular speed (the rate of rotation) directly affects the linear speed (how fast a horse travels along its path).
Illustration of Centripetal Acceleration in Terms of Angular Speed
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Centripetal acceleration can also be expressed in terms of angular speed as ac = ΟΒ²R.
Detailed Explanation
Centripetal acceleration can be derived from the angular speed. When rewritten, the equation ac = ΟΒ²R shows that acceleration is proportional to the square of the angular speed and the radius of the circular path. This emphasizes that an increase in either the angular speed or the radius will impact the centripetal acceleration.
Examples & Analogies
For a spinning carousel ride, if you spin it faster (increasing angular speed), the centripetal acceleration (the force pulling you inward on the ride) also increases. Conversely, if the carousel has a larger radius, such as moving from the center to the edge, the same rotation speed results in greater centripetal acceleration, explaining why the forces feel stronger at the edges.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Uniform Circular Motion: Constant speed in a circular path.
-
Centripetal Acceleration: Always directed towards the center of the circle, given by \( a_c = \frac{v^2}{R} \).
-
Relationship between linear speed and angular speed: \( v = R \omega \).
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
When a car rounds a curve at a constant speed, it experiences uniform circular motion.
-
A satellite orbiting the Earth maintains a uniform circular motion around the planet.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
Around the circle, fast and fleet, centripetal pulls, makes movement neat.
π Fascinating Stories
-
Imagine a car going around a racetrack, the faster it goes, the more it needs to pull inwards to keep from spinning out, just like a curious cat chasing a toy on a string.
π§ Other Memory Gems
-
Remember 'Centripetal is Center Seeking' to remember the direction of centripetal acceleration.
π― Super Acronyms
C.A.R. - Centripetal Acceleration is Related to Velocity squared and Radius.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Uniform Circular Motion
Definition:
Motion in a circular path at a constant speed, resulting in a continuous change of velocity due to changing direction.
-
Term: Centripetal Acceleration
Definition:
Acceleration directed towards the center of a circular path, calculated as \( a_c = \frac{v^2}{R} \).
-
Term: Angular Speed
Definition:
The rate of change of angular displacement, expressed as radians per unit time.
-
Term: Linear Speed
Definition:
The constant speed along the circular path, calculated as the distance traveled per unit of time.
-
Term: Radius
Definition:
The distance from the center of the circle to any point on its circumference.