Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Position Vectors
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we are going to learn about position vectors. Can anyone tell me what a position vector is?
Is it the way we describe where an object is located?
Exactly! A position vector indicates the position of an object in space relative to a chosen origin. We represent it using the symbol r. For instance, if our origin is point O and the object is at point P, then the position vector is written as OP = r.
So, if the object moves, does the position vector change?
Yes, it changes with the objectβs position. The position vector is dynamic as it responds to changes in location.
Can we use different points as an origin?
Absolutely! You can choose any point as your origin; however, consistency is key for your analysis.
In summary, a position vector helps us pinpoint an object's location relative to the origin.
Understanding Displacement Vectors
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, letβs discuss displacement vectors. What happens when an object moves from point P to point P'?
We measure how far it moved between those two points right?
Yes, precisely! The displacement vector, denoted as PP', is the straight line connecting the initial position and the final position.l
And this doesnβt depend on how the object got there, right?
Correct! The displacement vector solely considers the initial and final positions, making it independent of the actual path taken.
So, if I travel from point A to B in a zigzag way or a straight line, my displacement remains the same?
Exactly! And remember, the magnitude of the displacement is always less than or equal to the path length.
In summary, we use displacement vectors to understand the shortest distance between the starting and ending points.
Significance of Vectors in Motion
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
So, why are position and displacement vectors so important in motion analysis?
They help us describe where objects are and how they move.
Exactly! Vectors, particularly position and displacement, are crucial for representing motion in a clear and precise manner.
Do we use them when discussing velocity and acceleration too?
Yes! Velocity is a vector quantity that indicates speed and direction, while acceleration tells us how velocity changes over time.
So, understanding these vectors is foundational for future topics in motion?
Absolutely! Mastery of position and displacement vectors sets the stage for a deeper understanding of various motion concepts.
In summary, understanding vectors empowers us to describe and analyze motion fully.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the concepts of position and displacement vectors are explained. The position vector describes the location of an object in relation to a defined origin, while the displacement vector represents the shortest path between two positions, highlighting that it is independent of the path taken. This foundational understanding is crucial for analyzing the motion of objects in two-dimensional space.
Detailed
Position and Displacement Vectors
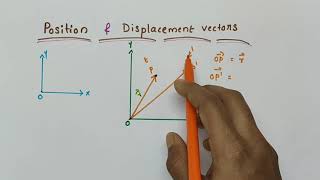
In physics, vectors play a crucial role in understanding motion and positioning within a coordinate system. Specifically, the position vector signifies the position of an object at a certain time relative to an origin, typically denoted as \( O \). For an object located at point \( P \), the position vector \( \mathbf{r} \) is represented as \( \overrightarrow{OP} = \mathbf{r} \).
When an object moves from point \( P \) to another point \( P' \), the change in its position is captured by the displacement vector, defined as \( \overrightarrow{PP'} \). This vector points directly from the object's initial to its final position and is mathematically represented as:
\[ \overrightarrow{PP'} = \overrightarrow{P'} - \overrightarrow{P} \]
One of the essential properties of the displacement vector is that it does not depend on the path taken between the two points, which sets it apart from distances covered during the journey. Therefore, the magnitude of the displacement is always less than or equal to the actual length of the path traveled between the two points. Understanding these concepts is pivotal for further discussions on motion in a plane, as they provide foundational knowledge for analyzing both linear and non-linear movements in two-dimensional space.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Choosing the Origin
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
To describe the position of an object moving in a plane, we need to choose a convenient point, say O as origin.
Detailed Explanation
In physics, when dealing with motion in two dimensions, it's crucial to establish a reference point, called the origin. This origin serves as a starting point for measuring the position of an object. By convention, we often label this point as O. This helps in systematically defining locations in the space we are analyzing.
Examples & Analogies
Think of a map of a city. The origin can be likened to a landmark like a central park or town square from which all other locations are measured. Just like you give directions from a known spot, in physics, we begin with a defined origin to describe the position of objects.
Position Vectors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let P and Pβ² be the positions of the object at time t and tβ², respectively. We join O and P by a straight line. Then, OP is the position vector of the object at time t. An arrow is marked at the head of this line. It is represented by a symbol r, i.e. OP = r. Point Pβ² is represented by another position vector, OPβ² denoted by rβ².
Detailed Explanation
The position of an object in a plane can be represented mathematically by vectors. When we have an object at point P at time t, we can draw a straight line from our origin O to point P; this line is known as the position vector and is denoted by r. Similarly, if the object is at a new position Pβ² at a later time tβ², we can draw another line from O to Pβ², which represents the position vector rβ². These vectors encapsulate both the direction and distance of the object's position from the origin.
Examples & Analogies
Imagine you are in a large park. If you start at the entrance (the origin) and walk straight to the fountain (point P), you can visualize the direct path you took as a vector pointing towards the fountain. If you then walk over to a statue (point Pβ²), you could represent your new position with another vector from the park entrance to the statue.
Magnitude and Direction of Position Vectors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The length of the vector r represents the magnitude of the vector and its direction is the direction in which P lies as seen from O.
Detailed Explanation
Every vector has two essential characteristics: magnitude and direction. The magnitude of a position vector refers to its length, which represents the distance between the origin O and the point P. The direction of the vector indicates where point P is located relative to the origin O. Therefore, by examining the position vector, we can understand both how far the object is from the reference point and in which direction it lies.
Examples & Analogies
If we return to our park example, the distance from the entrance to the fountain gives us the magnitude, while the direction can be thought of as the compass bearing we would take to reach the fountain from the entrance. This way, we know precisely where each point is located.
Displacement Vector
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If the object moves from P to Pβ², the vector PPβ² (with tail at P and tip at Pβ²) is called the displacement vector corresponding to motion from point P (at time t) to point Pβ² (at time tβ²).
Detailed Explanation
The displacement vector describes the change in position of an object. When an object moves from point P to point Pβ², we can visualize this transition as a new vector, which we denote as PPβ². This vector is different from the position vectors because it specifically represents how far and in what direction the object has moved from its initial position to its new position, focusing solely on the change rather than the entire path taken.
Examples & Analogies
Imagine you are in a game of tag. When you start at one tree (point P) and run to another tree further away (point Pβ²), the distance you directly cover and the straight path you take represents your displacement vector. If you took a winding path around the park, your displacement would still just account for the straight line distance between the two trees, regardless of how long your actual path was.
Displacement Independence of Path
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The displacement vector is the straight line joining the initial and final positions and does not depend on the actual path undertaken by the object between the two positions.
Detailed Explanation
One of the key properties of displacement is that it is solely concerned with the initial and final positions of an object. Whether an object takes a long, winding road or a straight path to reach its destination, the displacement vector will always be drawn as a straight line connecting the starting point to the endpoint. This simplification allows us to concentrate on the overall change in position rather than the specifics of the motion itself.
Examples & Analogies
Consider a road trip where you drive from one city to another. The distance you drive (the path length) might be longer if you detour around a lake or through various towns. However, your displacement merely measures the straight-line distance from the starting city to the destination city. Hence, even if your trip takes hours due to detours, your displacement remains constant based on the cities' locations.
Magnitude of Displacement
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Therefore, the magnitude of displacement is either less or equal to the path length of an object between two points. This fact was emphasised in the previous chapter also while discussing motion along a straight line.
Detailed Explanation
The relationship between displacement and path length is significant in physics. The magnitude of the displacement vector will always be less than or equal to the total distance traveled (path length) by the object. This principle stems from the fact that straight-line distance (displacement) is the shortest route between two points, while the actual path length may involve various turns and deviations, lengthening the travel distance overall.
Examples & Analogies
If you think about walking to a friendβs house, the straight-line distance might be only 2 kilometers. However, if you take a scenic route through the park and around other streets totaling 2.5 kilometers, your path length is longer than your displacement. Whether you prefer a straight path or a detour, both travel methods eventually connect you to your friend!
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Position Vector: Indicates the position of an object in relation to an origin.
-
Displacement Vector: Represents the shortest path between two points, independent of the journey taken.
-
Magnitude: The numerical value indicating the length of a vector.
-
Path Length: The actual distance traveled along the route taken.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An object moves from point P(2, 3) to point P'(5, 7). The position vector is represented as r = OP, while the displacement vector is PP' = P' - P.
-
If a person walks from home to a store in a zigzag pattern and back home, the path length is greater than the displacement which is zero, as the initial and final positions are the same.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
In every vector's game, position points the same; displacement draws the line, through a path that's just fine.
π Fascinating Stories
-
Imagine a bird flying from a tree to a meadow. Its position vector points to the tree, while the displacement vector shows the direct line between the tree and the meadow.
π§ Other Memory Gems
-
For position use 'P' for Place; for displacement, think of it as 'D' for Direct line.
π― Super Acronyms
Remember PPTD
- Position tells Where
- and Displacement tells How Far in a Straight Line.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Position Vector
Definition:
A vector that defines the position of an object relative to a chosen origin.
-
Term: Displacement Vector
Definition:
A vector that represents the shortest path from the initial to the final position of an object.
-
Term: Magnitude
Definition:
The length or size of a vector, which represents its numerical value.
-
Term: Path Length
Definition:
The total distance traveled by an object along its journey.
-
Term: Vector
Definition:
A quantity that has both magnitude and direction.