Nature of electromagnetic waves
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Electromagnetic Waves
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today's topic is the nature of electromagnetic waves. Can anyone tell me what electromagnetic waves are?

Aren't they waves that have both electric and magnetic fields?

Exactly! Electromagnetic waves consist of oscillating electric and magnetic fields that are perpendicular to each other. Can you think of what this means about their propagation?

Does that mean they can travel through space?

Yes, they can! In fact, they propagate through a vacuum, unlike sound waves which need a medium. This property is essential for understanding how we receive signals from far away.

Can the speed of these waves change depending on the medium?

Great question! The speed of electromagnetic waves changes based on the medium's permittivity and permeability. We'll dive deeper into that shortly.

To remember this, think of 'EMW' for Electromagnetic Wave. Next, let's discuss how these fields interact with each other.
The Relationship Between Electric and Magnetic Fields
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

"In an electromagnetic wave, the oscillating electric field E is represented as: $$E = E_0 ext{sin}(kz -
Propagation Through Different Mediums
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now that we understand the equations, how do electromagnetic waves behave in different media?

I think their speed changes?

That's right! The speed changes depending on the medium's properties, specifically its permittivity (ε) and permeability (μ). We express it as: $$v = \frac{1}{\sqrt{\mu\epsilon}}$$.

So the speed of light is a constant in a vacuum?

Correct! The speed of light in a vacuum is approximately $$3 × 10^8 m/s$$ and this speed is independent of wavelength. This means all electromagnetic waves travel at this speed in space.

Is that why we can see light from the stars? Because it travels through the vacuum?

Yes! And this trait allows us to see distant galaxies and receive signals from satellites. Remember, 'light travels faster through less dense mediums.'
Applications of Electromagnetic Waves
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s talk about the application of electromagnetic waves. Can anyone name a some real-life examples?

Radio and television?

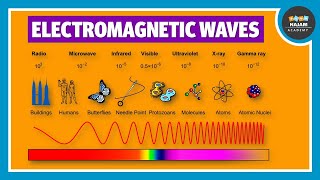
Absolutely! Radio waves are crucial for communication. Another example is light, which serves essential functions, like photosynthesis.

What about microwaves?

Great point! Microwaves are used in modern ovens to heat food by exciting water molecules. As they oscillate, they produce heat.

I read that X-rays are also part of this spectrum!

Yes! X-rays are used in medicine to visualize the inside of our bodies. Remember: 'Electromagnetic waves are everywhere in technology—acting as a bridge for information and energy!'
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
Electromagnetic waves, as highlighted by Maxwell's equations, have electric and magnetic fields that are orthogonal to each other and to the direction of wave propagation. The section explains how these waves can propagate through a vacuum, the relationship between their fields, and introduces equations describing their behavior.
Detailed
Nature of Electromagnetic Waves
Electromagnetic waves, as derived from Maxwell's equations, are characterized by their oscillating electric and magnetic fields that are perpendicular to one another and to the direction of propagation. The electric field
E and magnetic field B in the wave obey specific sinusoidal equations, where each field varies with respect to distance and time, defined as:
-
Electric Field:
$$E = E_0 ext{sin}(kz -
u t)$$
where \(E_0\) is the amplitude, and \(k\) is the wave number related to the wavelength \(\lambda\), given by \(k = \frac{2\pi}{\lambda}\). -
Magnetic Field:
$$B = B_0 ext{sin}(kz -
u t)$$
Similarly, the fields oscillate with a certain angular frequency \(\omega\) also related to the speed of light \(c\). The relationship between the speed of the electromagnetic wave, its frequency, and wavelength is given by: -
$$c = \lambda
u$$
The section elaborates on how these waves are unique in that they can propagate through a vacuum without a material medium, yet can still travel through different media, adjusting their velocity based on the medium's permittivity and permeability. The wave equations reveal that the electric and magnetic fields are not only related in magnitude but also interact to perpetuate the wave's propagation through oscillating charges.
Youtube Videos









Audio Book
Dive deep into the subject with an immersive audiobook experience.
Perpendicular Nature of E and B Fields
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
It can be shown from Maxwell’s equations that electric and magnetic fields in an electromagnetic wave are perpendicular to each other, and to the direction of propagation.
Detailed Explanation
Maxwell’s equations establish that in an electromagnetic wave, the electric field (E) and the magnetic field (B) are always perpendicular to each other and also to the direction the wave travels. This means if the wave is moving in one direction, the electric and magnetic fields are oriented in two other directions, forming a right-angle relationship. This feature is crucial as it defines how electromagnetic waves propagate through space.
Examples & Analogies
Imagine a flag waving in the wind. The direction the flag is waving (horizontal) is like the direction of the wave propagation, while the up-and-down movement of the flag represents the electric field, and a side-to-side movement represents the magnetic field. The flag cannot wave in a different direction than the wind pushes it, just as the electric and magnetic fields cannot exist in the same direction as the wave is traveling.
Sinusoidal Variation of E and B
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In Fig. 8.3, we show a typical example of a plane electromagnetic wave propagating along the z direction (the fields are shown as a function of the z coordinate, at a given time t). The electric field E is along the x-axis, and varies sinusoidally with z, at a given time. The magnetic field B is along the y-axis, and again varies sinusoidally with z.
Detailed Explanation
In a typical electromagnetic wave, as it moves through space, both the electric field and the magnetic field change in a sinusoidal manner over space and time. This means that if you were to observe a wave at a fixed point, the intensity of the electric field would go up and down in a smooth, wave-like pattern, similar to how ocean waves rise and fall. The same happens for the magnetic field but at 90 degrees to the electric field, retaining the perpendicularity.
Examples & Analogies
Think of sound waves traveling through the air, where the compressions and rarefactions of the wave occur in a pattern. Just as sound waves create regions of high and low pressure, electromagnetic waves create peaks and troughs in electric and magnetic fields at various points in space as they propagate, but without needing any medium to travel through.
Wave Properties and Equations
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
We can write E and B as follows:
E = E₀ sin(kz - ωt) [8.7(a)]
B = B₀ sin(kz - ωt) [8.7(b)]
Detailed Explanation
These equations express how the electric field (E) and magnetic field (B) are mathematically connected to the wave's progress. Here, E₀ and B₀ are the maximum strengths of the respective fields, 'k' is the wave number (related to wavelength), 'ω' is the angular frequency, 'z' represents the position, and 't' represents time. These equations illustrate that both fields oscillate at the same frequency and are in sync as they propagate through space.
Examples & Analogies
Imagine a swing set where each swing moves back and forth: as one swing (electric field) rises, so does another (magnetic field), both following the same rhythmic pattern. Just as the swings reach their highest point at the same time, the electric and magnetic fields reach their peak strengths together in the wave equation.
Relationship Between Frequency and Wavelength
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Using Eqs. [8.7(a) and (b)] for E and B and Maxwell’s equations, one finds that ω = ck, where, c = 1/√(μ₀ε₀).
Detailed Explanation
This equation reveals a foundational connection in wave dynamics; it states that the angular frequency (ω) of the wave is directly proportional to its wave number (k), which in turn is related to the speed of light (c). In simple terms, it shows how changes in frequency influence wavelengths and vice versa, underscoring the wave nature of electromagnetic phenomena. The speed of electromagnetic waves in a vacuum is constant, elucidating that all electromagnetic waves, regardless of their specific frequency, travel at this speed.
Examples & Analogies
Think of a concert where the band plays different tunes. The faster the tempo (frequency), the shorter the individual notes (wavelengths). Regardless of the tune, the concert keeps the same pace of play (speed of light), demonstrating that as we change one aspect (frequency of the tune), the other aspect (length of notes) must adjust while maintaining the overall rhythm.
Electric and Magnetic Field Magnitudes
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
It is also seen from Maxwell’s equations that the magnitude of the electric and the magnetic fields in an electromagnetic wave are related as B = (E₀/c),
Detailed Explanation
This relationship illustrates that for a given electromagnetic wave, the strength of the magnetic field (B) is directly dependent on the strength of the electric field (E₀) when measured at their peak values, with 'c' being the speed of light. This signifies not only a direct connection but also helps in predicting one field based on the other, thus emphasizing the interdependence of electric and magnetic phenomena in these waves.
Examples & Analogies
Think of a dance routine where every dance move (magnetic field) corresponds to a specific position or gesture (electric field). The intensity of the dance performance reflects the electric fields, while the synchronization of the dancers showcases the magnetic fields. If one dancer moves more dynamically, the other must follow suit to match the choreography, hence illustrating their interconnectedness.
Key Concepts
-
Electromagnetic Waves: Composed of oscillating electric and magnetic fields perpendicular to each other.
-
Wave Propagation: Waves travel through a vacuum and their speed depends on the medium.
-
Maxwell's Equations: Set of equations that describe how electric and magnetic fields interact and give rise to electromagnetic waves.
-
Sinusoidal Behavior: The electric and magnetic fields vary sinusoidally in space and time.
-
Relationship of Fields: The electric field is related to the magnetic field via the speed of light (c).
Examples & Applications
In a vacuum, electromagnetic waves travel at the speed of light, approximately 3 × 10^8 m/s.
The electric field component of an electromagnetic wave can be described by the equation E = E_0 sin(kz - ωt).
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
E and B, harmoniously sway, through space they travel, come what may.
Stories
Imagine electric and magnetic fields dancing in sync, creating beautiful waves that travel through the cosmos, communicating across light years.
Memory Tools
Remember: Every Nice Day - Electric is perpendicular to Magnetic and Direction.
Acronyms
EMW stands for Electromagnetic Wave, summarizing the core concept of the section.
Flash Cards
Glossary
- Electromagnetic Waves
Waves of oscillating electric and magnetic fields that propagate through space.
- Wave Number (k)
The number of wavelengths per unit distance, given as k = 2π/λ.
- Amplitude
The maximum value of the electric or magnetic field in the wave.
- Permittivity (ε)
A measure of how an electric field interacts with a medium.
- Permeability (μ)
A measure of how a magnetic field interacts with a medium.
- Speed of Light (c)
A fundamental constant representing the speed at which light travels in a vacuum, approximately 3 × 10^8 m/s.
Reference links
Supplementary resources to enhance your learning experience.
