Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Maxwell's Equations and Displacement Current
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're going to discuss Maxwell's pivotal discovery about displacement current. Can anyone remind me what displacement current relates to?
I think it's about how changing electric fields can create a magnetic field?
Exactly! Maxwell identified that a time-varying electric field produces a magnetic field, which was missing in Ampere's Law. This led to the introduction of the displacement current. Can anyone explain what the formula looks like?
Is it something like i_d = Ξ΅β * dΞ¦_E/dt?
Spot on! Displacement current is analogous to conduction current. Just remember, where there's a changing electric field, there is associated magnetic activity as well. Let's keep this in mind as we move forward!
Electromagnetic Waves
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let's examine electromagnetic waves themselves. Who can tell me what characterizes these waves?
They have an electric field and magnetic field that oscillate, right?
Correct! These fields are perpendicular to one another and the direction of propagation. Can anyone describe how we represent them mathematically?
I think we can represent the electric field as E = Eβ * sin(kz - Οt) and the magnetic field as B = Bβ * sin(kz - Οt).
Exactly! This representation illustrates both the wave-like nature and the relationship between electric and magnetic fields. Let's not forget the speed of these waves, which is the speed of light, denoted by 'c'.
The Electromagnetic Spectrum
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Lastly, let's get familiar with the electromagnetic spectrum. Can anyone mention some regions of this spectrum?
There's radio waves, visible light, and gamma rays?
Absolutely! The spectrum covers various wavelengths, indicating different types of electromagnetic radiation. Remember the mnemonic 'Really Men In Vegas Use eX-ray Guns' to recall the parts of the spectrum: Radio, Microwave, Infrared, Visible, Ultraviolet, X-ray, Gamma!
That's helpful, because it highlights the relationship between frequency and wavelength.
Exactly! The wavelengths dictate their interactions with matter and lead to various applications. It's critical to recognize how technologies leverage these properties.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Maxwell's conclusions about displacement current, electromagnetic waves, and their interactions with matter are critical in understanding electromagnetism. The section highlights the relationship between electric and magnetic fields, how they propagate, and the implications of these properties across the electromagnetic spectrum.
Detailed
Detailed Summary
Maxwell's work revealed critical insights into the behavior of electric and magnetic fields, culminating in the concept of displacement current. A changing electric field generates a magnetic field, which allows the existence of electromagnetic waves. In essence, these waves consist of oscillating electric (E) and magnetic (B) fields, perpendicular to each other and the direction of propagation.
He formulated equations that unite these phenomena, demonstrating that light itself is an electromagnetic wave traveling at the speed of light in a vacuum (c = 3 Γ 10^8 m/s). This revelation significantly affected technology and science since it laid the groundwork for modern electromagnetic theory.
In summary, electromagnetic waves display sinusoidal behavior and are characterized by their wavelength and frequency. The interplay of these waves underlies their interaction with matter and represents the backbone of various technologies today.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Displacement Current and Ampere's Law
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Maxwell found an inconsistency in the Ampereβs law and suggested the existence of an additional current, called displacement current, to remove this inconsistency. This displacement current is due to time-varying electric field and is given by
i = Ξ΅β (dΞ¦_E/dt)
and acts as a source of magnetic field in exactly the same way as conduction current.
Detailed Explanation
Maxwell discovered that Ampere's law, which relates electric currents to magnetic fields, had a flaw when considering situations with changing electric fields. He proposed a new concept called 'displacement current' to resolve this flaw. This displacement current is not due to moving charges, like a regular current, but is generated by a changing electric field. Mathematically, it's expressed as Ξ΅β (dΞ¦_E/dt), where Ξ΅β is the permittivity of free space, and dΞ¦_E/dt represents the rate of change of electric flux. Essentially, this means that a changing electric field can create a magnetic field, similar to how a conventional current does.
Examples & Analogies
Think of it like a river that flows smoothly under normal conditions (conduction current). However, if it starts to swell and change its flow direction rapidly (time-varying electric field), new paths (displacement current) can form that also contribute to the overall flow (magnetic field). Just like both currents affect the environment, so do conduction and displacement currents affect the creation of magnetic fields.
Production of Electromagnetic Waves
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- An accelerating charge produces electromagnetic waves. An electric charge oscillating harmonically with frequency n, produces electromagnetic waves of the same frequency n. An electric dipole is a basic source of electromagnetic waves.
Detailed Explanation
Electromagnetic waves are generated when charged particles, like electrons, accelerate. If these charges oscillate or move back and forth regularly (i.e., with a certain frequency 'n'), they create oscillating electric and magnetic fields that propagate through space as electromagnetic waves. The relationship is direct: the frequency of the wave created corresponds exactly to the frequency of the oscillating charge. A good example of this is an electric dipole, which consists of two equal but opposite charges separated by a small distance. Whenever the dipole's charges oscillate, they emit electromagnetic waves.
Examples & Analogies
Imagine strumming a guitar string; as you move your fingers back and forth, sound waves are produced in the air. Similarly, when a charge oscillates, it creates electromagnetic waves that travel like sound waves, but through electric and magnetic fields instead of air.
Experimental Verification by Hertz
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Electromagnetic waves with wavelength of the order of a few metres were first produced and detected in the laboratory by Hertz in 1887. He thus verified a basic prediction of Maxwellβs equations.
Detailed Explanation
Heinrich Hertz was the first to experimentally confirm the existence of electromagnetic waves envisioned by Maxwell. In 1887, he generated and detected radio waves (which are a type of electromagnetic wave) in a laboratory setting. Hertz's experiments showed that these waves could travel through space and exhibited properties similar to visible light, such as reflection and refraction, thus proving Maxwell's theoretical predictions were correct.
Examples & Analogies
Think of Hertz's experiments as an exciting discovery in a new realm. It's like a scientist first proving that a new species of animal exists after only theorizing about it. Initially, people may have doubted that such 'invisible' waves could exist, but Hertz's experiments opened the door to a new understanding of light and communication.
Characteristics of Electric and Magnetic Fields in Waves
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Electric and magnetic fields oscillate sinusoidally in space and time in an electromagnetic wave. The oscillating electric and magnetic fields, E and B are perpendicular to each other, and to the direction of propagation of the electromagnetic wave. For a wave of frequency n, wavelength l, propagating along z-direction, we have
E = Eβ sin(kz - Οt)
B = Bβ sin(kz - Οt)
They are related by Eβ/Bβ = c.
Detailed Explanation
In an electromagnetic wave, the electric field (E) and magnetic field (B) oscillate in a synchronized manner, changing values as they propagate through space. Their directions are mutually perpendicular to each other and to the direction in which the wave travels. We can mathematically describe this oscillation with sine functions where E and B have their own maximum values (Eβ and Bβ). The speed of light (c) is a constant that relates the strength of these fields, illustrating their interconnected nature.
Examples & Analogies
Visualizing this is akin to the motion of a sine waveβlike waving a flag. The flag flaps (oscillates) side to side (electric field), while the pole itβs attached to stands tall and steady (magnetic field). Both parts are essential to the overall motion and together create a wave traveling away from the flagpole.
Speed of Electromagnetic Waves
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- The speed c of electromagnetic wave in vacuum is related to Ξ΅β and ΞΌβ (the free space permeability and permittivity constants) as follows: c = 1/β(Ξ΅βΞΌβ). The value of c equals the speed of light obtained from optical measurements. Light is an electromagnetic wave; c is, therefore, also the speed of light. Electromagnetic waves other than light also have the same velocity c in free space.
Detailed Explanation
The speed at which electromagnetic waves travel in a vacuum is a fundamental constant, denoted by 'c' (approximately 3 x 10βΈ m/s), and links the electric and magnetic properties of free space through the permittivity (Ξ΅β) and permeability (ΞΌβ). This relationship highlights that all electromagnetic wavesβwhether visible light or radio wavesβshare the same speed in vacuum, emphasizing their unified nature.
Examples & Analogies
Consider the speed limit on a highway. Just as all types of vehicles (cars, trucks, motorcycles) can travel the same speed under ideal conditions, all electromagnetic waves can propagate through vacuum at the speed of light without losing their unique identities. Whether itβs light illuminating your room or radio waves transmitting your favorite music, they all move uniformly in empty space.
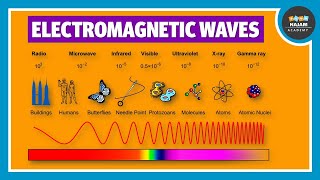
The Electromagnetic Spectrum
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- The spectrum of electromagnetic waves stretches, in principle, over an infinite range of wavelengths. Different regions are known by different names; Ξ³-rays, X-rays, ultraviolet rays, visible rays, infrared rays, microwaves and radio waves in order of increasing wavelength from 10β»Β² m or 10β»ΒΉΒ² m to 10βΆ m. They interact with matter via their electric and magnetic fields which set in oscillation charges present in all matter. The detailed interaction and so the mechanism of absorption, scattering, etc., depend on the wavelength of the electromagnetic wave, and the nature of the atoms and molecules.
Detailed Explanation
The electromagnetic spectrum encompasses all frequencies and wavelengths of electromagnetic radiation, from very short gamma rays to very long radio waves. Each type of wave interacts with matter differently based on its energy and wavelength. For instance, gamma rays can penetrate tissues while radio waves may pass through structures without interaction. This variation in interactions leads to diverse technological applications, depending on the frequencyβlike medical imaging with X-rays versus communication systems with radio waves.
Examples & Analogies
Imagine a toolbox filled with various tools that you use for different tasks. The toolbox represents the electromagnetic spectrum. Just like you'd use a hammer for pounding nails (e.g., X-rays for imaging) and a screwdriver for turning screws (e.g., radio waves for communication), different electromagnetic waves serve unique purposes based on their characteristics. Understanding and utilizing this 'toolbox' allows us to innovate and find solutions in technology, medicine, and science.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Maxwell's Equations: Foundation of electromagnetism, relating electric and magnetic fields.
-
Displacement Current: Key to understanding how changing electric fields contribute to magnetic fields.
-
Electromagnetic Waves: Formed from oscillating electric and magnetic fields, showing properties of both.
-
Electromagnetic Spectrum: Range of electromagnetic waves categorized by wavelength and frequency.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example: A radio wave with a frequency of 100 MHz has a wavelength of about 3 meters.
-
Example: Light from a common bulb emits various wavelengths that fall within visible spectrumβthe range we can see.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
From light to sound, in waves they blend, it's energy that travels - on it we depend.
π Fascinating Stories
-
Imagine a dance where electric fields twirl and magnetic companions follow. Together they travel through space, creating waves that carry energy from one place to another, like a torch lighting up the night sky.
π§ Other Memory Gems
-
Remember 'Really Men In Vegas Use eX-ray Guns' to recall parts of the electromagnetic spectrum: Radio, Microwave, Infrared, Visible, Ultraviolet, X-ray, Gamma.
π― Super Acronyms
Use 'EMW' for Electromagnetic Waves to remember they consist of both electric and magnetic components.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Maxwell's Equations
Definition:
A set of four equations that describe how electric and magnetic fields interact and are generated by charges and currents.
-
Term: Displacement Current
Definition:
A term introduced by Maxwell representing a type of current created by a changing electric field, which contributes to the magnetic field in addition to conduction current.
-
Term: Electromagnetic Wave
Definition:
A wave produced by the oscillation of electric and magnetic fields, which propagate through space.
-
Term: Electromagnetic Spectrum
Definition:
The range of all types of electromagnetic radiation, characterized by their wavelengths and frequencies.