Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Wavefronts and Huygens' Principle
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we will begin by discussing the concept of a wavefront. Can anyone tell me what a wavefront is?
Isn't it the surface over which the wave has a constant phase?
Exactly! A wavefront is indeed a surface of constant phase. When we consider how waves propagate, Huygens' Principle becomes very important. It tells us that every point on a wavefront can be seen as a source of new wavelets that spread out in all directions.
So, how do we use these wavelets to find out where the wavefront will be later?
Great question! To determine the new wavefront, we draw the envelope of these secondary wavelets, essentially creating a new wavefront at a future time.
Can you give us an example of this?
Sure! Imagine dropping a stone in a calm pool of water. The ripples you see are actually circular wavefronts emanating from the point of impact.
So, the circular ripples represent the wavefronts?
Correct! Each of the points on the circular wavefront can be treated as sources of secondary wavelets propagating outward.
In this way, we can visualize how the wavefront expands over time.
Reflection and Refraction Using Huygens' Principle
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's explore how we can apply Huygens' Principle to understand reflection and refraction. Who can summarize what happens to light during these phenomena?
When light reflects, it bounces off a surface, and when it refracts, it bends as it passes into a different medium.
Correct! By using Huygens' Principle, we know that the wavefront contributes to both phenomena by analyzing secondary wavelets. For example, upon striking a reflective surface, we can consider the behavior of wavelets at the interface.
And how about refraction?
Good point! When light goes from one medium to another, like air to water, the change in speed causes the wavefront to bend. According to Huygens' Principle, we can visualize how the wavelet structures produced in both media contribute to this bending.
What does that mean for the speed of light in different media?
When light enters a denser medium, it slows down, and when it transitions to a rarer medium, it speeds up. Huygens' Principle helps illustrate these changes through the construction of the wavefront.
Wavefront Shapes and Their Definitions
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Letβs discuss the shapes of wavefronts. Can anyone tell me the difference between a spherical wavefront and a plane wavefront?
A spherical wavefront spreads out from a point source like the ripples in water, while a plane wavefront is like the wavefront of light from a distant star, appearing flat.
Excellent observation! A small section of a spherical wavefront can appear as a plane wave at a large distance, making it easier to analyze in geometrical optics. This approximation simplifies our calculations.
And we can always use Huygens' Principle for both types of wavefronts, right?
Absolutely! Huygens' Principle applies universally to describe the secondary wavelets for any wavefront shape.
Does this mean we can construct any wavefront shape using Huygens' Principle?
Yes, we can! As long as we define the initial wavefront, we can apply Huygens' construction to derive its future positions.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Huygens' Principle provides a method to construct the shape of a new wavefront using the circular wavelets from each point on the initial wavefront. It is fundamental in explaining the laws of reflection and refraction of light, revealing that light behaves as a wave and not merely as rays.
Detailed
Huygens' Principle
Huygens' Principle asserts that every point on a wavefront serves as a source of secondary wavelets, which propagate in all directions at the same speed as the original wave. To construct the new wavefront at a given future time, one draws the envelope of these secondary wavelets. This geometric construction helps predict the evolution of wavefronts over time. For instance, a spherical wave emanating from a point source can be visualized as a series of spherical wavelets expanding outward, leading to an overall spherical wavefront.
This principle clarifies the concepts of reflection and refraction in wave optics. By employing Huygens' Principle, various wavefront configurations can be analyzed, such as spherical and plane waves, offering insights into the behavior of light as it travels through different media. In addition, the principle underscores the importance of wave behavior in understanding the speed of light in various media, laying the groundwork for further discussions on interference and diffraction in the following sections.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Wavefront
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
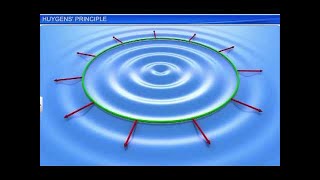
We would first define a wavefront: when we drop a small stone on a calm pool of water, waves spread out from the point of impact. Every point on the surface starts oscillating with time. At any instant, a photograph of the surface would show circular rings on which the disturbance is maximum. Clearly, all points on such a circle are oscillating in phase because they are at the same distance from the source. Such a locus of points, which oscillate in phase is called a wavefront; thus a wavefront is defined as a surface of constant phase.
Detailed Explanation
A wavefront is a surface over which an oscillating quantity, such as light or sound, has a constant phase. When a small object, like a stone, is thrown into a pond, it creates waves that move outward in circles. These circles represent wavefronts, with each point on the wavefront oscillating together at the same time, ensuring they are 'in phase'. Imagine it like a synchronized swimming team where all members move together, forming a perfect pattern.
Examples & Analogies
Think of wavefronts like the ripples that spread out when you throw a pebble into a calm pond. The circles of the ripples represent wavefronts, and at every point on a particular ripple, the water level is at the same height, all rising and falling together like a synchronized dance.
Types of Waves
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If we have a point source emitting waves uniformly in all directions, then the locus of points which have the same amplitude and vibrate in the same phase are spheres and we have what is known as a spherical wave. At a large distance from the source, a small portion of the sphere can be considered as a plane and we have what is known as a plane wave.
Detailed Explanation
When a sound or light source emits waves uniformly in all directions, these waves form spherical wavefronts, akin to balloons expanding outward from a central point. In far-away observations, the curvature of these spheres becomes negligible, and they can be approximated as 'plane waves', which are easier to analyze because they simplify the complex behavior of waves into a flat, two-dimensional representation.
Examples & Analogies
Consider how sound travels from a loudspeaker. Close to the speaker, sound waves are spherical as they spread out. However, far away, they can be seen as flat waves, similar to how the Earth's surface appears flat due to its vast size compared to our view.
Huygens Principle Overview
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, if we know the shape of the wavefront at t = 0, then Huygens principle allows us to determine the shape of the wavefront at a later time t. Thus, Huygens principle is essentially a geometrical construction, which given the shape of the wavefront at any time allows us to determine the shape of the wavefront at a later time.
Detailed Explanation
Huygens' Principle can be understood as a method for predicting the future position and shape of wavefronts. It suggests that every point on an existing wavefront serves as a source of new waves, known as secondary wavelets. These secondary waves spread out in all directions. By tracing the envelope of these secondary waves, you can determine how the overall wavefront will evolve over time.
Examples & Analogies
Imagine you are at the edge of a large pond and you see the ripples moving outward. If you drop more stones one after another, each ripple can be seen as a new point generating its own set of ripples. By observing how the ripples spread, you can effectively predict the overall shape of the water surface at any future time.
Constructing New Wavefronts
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us consider a diverging wave and let F F represent a portion of the spherical wavefront at t = 0. According to Huygens principle, each point of the wavefront is the source of a secondary disturbance, and the wavelets emanating from these points spread out in all directions with the speed of the wave.
Detailed Explanation
In this illustration of Huygens' Principle, we start with a known wavefront, termed FF, that is at a specific time. Each point on this wavefront emits new wavelets that expand outward. By considering the radii of these emitted wavelets, we can construct new wavefronts at future times based on their positions after they spread out for a certain distance.
Examples & Analogies
Imagine a group of people standing in a circle, each person starts tossing a ball simultaneously. The balls represent secondary waves. As each ball travels outward, the farthest points reached by the balls can help define a new boundary to show where the next circle of people will form as they get ready to throw.
Absence of Backwaves
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Huygens argued that the amplitude of the secondary wavelets is maximum in the forward direction and zero in the backward direction; by making this ad hoc assumption, Huygens could explain the absence of the backwave. However, this ad hoc assumption is not satisfactory and the absence of the backwave is really justified from more rigorous wave theory.
Detailed Explanation
Huygens introduced an assumption that only waves moving forward carry energy and intensity, hence there are no waves moving backwards. This simplification was useful for his initial theories but lacks complete accuracy for more complex wave behaviors. Rigorously, it has since been concluded through further studies in optical phenomena that while waves typically propagate outward, potential backward waves exist but are not observed under normal conditions.
Examples & Analogies
Think of a train on a track. When the train moves forward, it generates a sound that travels outward, but if the train were to reverse, you wouldn't hear that sound traveling back toward it in the same way. Huygens' initial approach is similar: while he focused on the waves moving away, the full understanding of sound waves considers that sounds can resonate backward too, depending on the environment.
Using Huygens Principle for Plane Waves
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In a similar manner, we can use Huygens principle to determine the shape of the wavefront for a plane wave propagating through a medium.
Detailed Explanation
Applying Huygens' Principle to plane waves allows us to analyze how these waves propagate in the same way as spherical waves. So when a plane wave travels through a medium, we can treat each point on its wavefront as a new emitter of wavelets. The process generates new wavefronts at future times that maintain the behavior and characteristics of the original wave.
Examples & Analogies
Think of a vast field of flowers swaying in the wind. Each bloom represents a point of the wavefront; as the wind moves, every flower sways in a rhythmic motion, simultaneously producing a wave-like effect across the field, allowing us to see the plane wave propagating through the sea of flowers.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Wavefront: A surface of constant phase for waves.
-
Huygens' Principle: Every point on a wavefront acts as a source of secondary wavelets.
-
Reflection: The return of waves upon striking a surface.
-
Refraction: The bending of waves when entering a new medium.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
When a stone is dropped into a pond, the ripples it creates form circular wavefronts.
-
Light from a distant star can be approximated as having plane wavefronts because of the vast distance from the observer.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
Waves spread out, round and free, Huygens' waves are key to see.
π Fascinating Stories
-
Imagine a crowd at a concert, sound waves ripple away from the stage β each person in the crowd represents a point on the wavefront sending out its own sound wave, just like Huygens' principle.
π§ Other Memory Gems
-
H.O.W. for Huygens' Principle β H for each point, O for outgoing wavelets, W for wavefront shape.
π― Super Acronyms
HYP for Huygens' Principle β H for Huygens, Y for Yearning to know, P for Propagation.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Wavefront
Definition:
A surface over which the phase of the wave is constant.
-
Term: Huygens' Principle
Definition:
Every point on a wavefront can be regarded as a source of secondary wavelets, which can be used to construct future wavefronts.
-
Term: Secondary Wavelets
Definition:
Small wavelets produced by each point on a wavefront, which propagate outward at the wave's speed.
-
Term: Reflection
Definition:
The bouncing back of light waves when they encounter a surface.
-
Term: Refraction
Definition:
The bending of light waves as they enter a different medium where their speed changes.