Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Polarisation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today we're going to discuss the concept of polarization. To start, can anyone tell me what they think polarization signifies in waves?
I think it refers to how waves can move in different directions?
Exactly! Polarization refers to the orientation of the oscillations of waves. For light, this can mean that the electric field oscillates in a specific direction.
How do we actually make light waves polarized?
Great question! Light can become polarized through materials called polaroids. They filter out light waves based on their orientation. If light passes through a polaroid, it becomes linearly polarized.
What happens if we have two polaroids?
Good observation! When you place a second polarizer in front of the first one, the intensity of transmitted light can change dramatically depending on how you orient the two polaroids in relation to each other.
That sounds similar to how sunglasses work!
Exactly! The same principle applies, as sunglasses often use polarized lenses to reduce glare. To summarize, polarization is all about the orientation of light waves. Remember: light can be unpolarized, and we can use devices like polaroids to control that polarization.
Malus's Law
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we understand what polarization is, letβs delve into Malus's Law, which gives us a mathematical framework for how polarisation affects light intensity.
What does Malus's Law state?
Malus's Law states that the intensity of the light transmitted through a polarizer is equal to the initial intensity divided by two, multiplied by the cosine squared of the angle between the light's electric field vector and the polarizer's pass axis. Formally, we express it as I = Iβ cosΒ²(ΞΈ).
Can we see an example of that?
Certainly! If unpolarized light with an intensity of 100 units passes through the first polaroid, only 50 units will come through. Now, if you add a second polaroid at 90 degrees to the first, nearly no light will come through because the intensity will be close to zero.
What if both polaroids are parallel?
In that case, the transmitted intensity will remain at 50 units through both polaroids. The orientation of the pass-axes plays a crucial role in the lightβs behavior.
So moving the polaroids changes the amount of light we see?
Exactly! The angle between the polaroids can reduce the transmitted light to almost none or maximize it, depending on their positions. Remember, 'Angle is crucial for intensity'.
Practical Applications of Polarisation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Letβs wrap up our discussion by exploring some practical applications of polarization in daily life.
Iβm curious, how is this used in technology?
Polarization is extensively used in sunglasses, cameras, and LCD screens. For instance, polaroid lenses can reduce glare from surfaces by filtering horizontally polarized light.
What about cameras? Iβve seen polarizing filters.
Good catch! In photography, polarizing filters enhance color saturation and reduce reflections, allowing for clearer images.
And LCD screens?
LCD screens use polarized light to control the visibility of images. They have two layers of polarizers, allowing specific orientations of light to be displayed.
This is awesome! I had no idea polarization had so many applications.
Absolutely! To summarize, polarization not only enhances visual experiences but also improves various technologies in our lives.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section introduces the concept of polarization, explaining how light waves can become polarized through specific methods such as passing through polaroids. It discusses the significance of light being transverse in nature, illustrating how polarization affects the intensity of light as it passes through multiple polaroid filters.
Detailed
Polarisation
Polarisation is a property of waves that describes the orientation of the oscillations perpendicular to the direction of wave propagation. In this section, we understand that if we take a long string and create transverse waves by moving one end up and down, we generate linearly polarized waves. These waves oscillate along a fixed plane, either in the x-y or x-z planes.
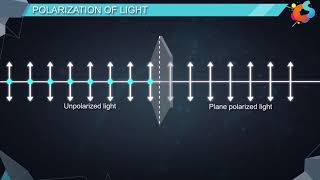
When considering light, which is made up of transverse electromagnetic waves, its polarization can occur through various methods. Natural light is generally unpolarized, meaning its electric field oscillates in multiple directions. A polaroid is a material that allows light waves oscillating in a particular direction to pass through while absorbing others. As the light passes through a polaroid, it becomes linearly polarized, where its electric field oscillates predominantly in the direction of the polaroid's pass-axis.
The intensity of light after passing through a polarizer can change significantly depending on the angle between the light's electric field vector and the pass-axis of the polaroid. Malus's law provides a quantitative description of this effect, stating that the intensity of transmitted light is proportional to the cosine square of the angle between these two vectors. Multiple polaroids can be stacked, and their relative orientations will greatly influence the intensity of light that eventually emerges, leading to interesting applications in technology and photography.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Transverse Waves and Polarisation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Consider holding a long string that is held horizontally, the other end of which is assumed to be fixed. If we move the end of the string up and down in a periodic manner, we will generate a wave propagating in the +x direction. Such a wave could be described by the following equation
\[y (x,t) = a \sin (kx β wt) \] (10.15)
where a and \( w (= 2\pi n) \) represent the amplitude and the angular frequency of the wave, respectively; further,
\[ \lambda = \frac{2\pi}{k} \] (10.16)
represents the wavelength associated with the wave. We had discussed propagation of such waves in Chapter 14 of Class XI textbook. Since the displacement (which is along the y direction) is at right angles to the direction of propagation of the wave, we have what is known as a transverse wave. Also, since the displacement is in the y direction, it is often referred to as a y-polarised wave. Since each point on the string moves on a straight line, the wave is also referred to as a linearly polarised wave. Further, the string always remains confined to the x-y plane and therefore it is also referred to as a plane polarised wave.
Detailed Explanation
In this chunk, we are introduced to the concept of transverse waves using the analogy of a string being manipulated. When you move a string up and down, you create waves that travel along its length. These waves can be described mathematically with equations that represent their displacement (how high or low they are at any point) over time and space. The term 'polarisation' refers to the direction of vibration in these waves. If the wave vibrates in one direction (like up and down), it is called linearly polarised. Understanding this concept is fundamental to grasping how light can behave as a wave and how it can be controlled and manipulated.
Examples & Analogies
Imagine a group of kids on a playground holding a long piece of rope. If one child pulls the rope up and down, the wave travels towards the other end of the rope. The motion represents a transverse wave. If all kids were to shake the rope up and down in the same way, the wave moving towards them is like a polarised wave, where all parts are moving in line with each other.
Understanding Unpolarised Waves
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In a similar manner we can consider the vibration of the string in the x-z plane generating a z-polarised wave whose displacement will be given by
\[ z (x,t) = a \sin (kx β wt) \] (10.17)
It should be mentioned that the linearly polarised waves [described by Eqs. (10.15) and (10.17)] are all transverse waves; i.e., the displacement of each point of the string is always at right angles to the direction of propagation of the wave. Finally, if the plane of vibration of the string is changed randomly in very short intervals of time, then we have what is known as an unpolarised wave. Thus, for an unpolarised wave the displacement will be randomly changing with time though it will always be perpendicular to the direction of propagation.
Detailed Explanation
This chunk discusses how to create a z-polarised wave in addition to the previously discussed y-polarised wave. When the vibrations of the wave change direction randomly β encompassing vertical, horizontal, and diagonal directions β the wave is described as unpolarised. An unpolarised wave has energy spread in multiple directions rather than a single plane. Understanding the difference between polarised and unpolarised waves is crucial, especially in optics, where light's behaviour changes based on its polarisation.
Examples & Analogies
Think of unpolarised light as a crowd of people at a music concert who are dancing in random directions β some are swaying, some jumping up and down, and some are simply standing. In contrast, polarised light is like a synchronized dance where everyone moves in the same direction at the same time. This organized movement represents the structured behaviour of linearly polarised waves.
Light as Transverse Waves
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Light waves are transverse in nature; i.e., the electric field associated with a propagating light wave is always at right angles to the direction of propagation of the wave. This can be easily demonstrated using a simple polaroid. You must have seen thin plastic like sheets, which are called polaroids. A polaroid consists of long chain molecules aligned in a particular direction. The electric vectors (associated with the propagating light wave) along the direction of the aligned molecules get absorbed. Thus, if an unpolarised light wave is incident on such a polaroid then the light wave will get linearly polarised with the electric vector oscillating along a direction perpendicular to the aligned molecules; this direction is known as the pass-axis of the polaroid.
Detailed Explanation
This part explains how light behaves as a transverse wave, specifically illustrating the concept using polaroids. A polaroid allows only certain orientations of light waves to pass through, effectively filtering out other orientations, which results in polarisation. When light travels through a polaroid, it becomes polarised because the polaroid's aligned molecules absorb the components of light that are not aligned with their direction. This property of light is essential for various applications, including sunglasses and cameras.
Examples & Analogies
Imagine wearing polarized sunglasses while in a car on a sunny day. They block out glare from the road by filtering light that is suddenly horizontal (unwanted reflections), allowing you to see better while driving. The sunglasses act like a polaroid, permitting only light that is aligned correctly, thus enhancing your vision unlike regular sunglasses.
Malus' Law and Transmission Through Polaroids
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Thus, if the light from an ordinary source (like a sodium lamp) passes through a polaroid sheet P it is observed that its intensity is reduced by half. Rotating P has no effect on the transmitted beam and transmitted intensity remains constant. Now, let an identical piece of polaroid P be placed before P . As expected, the light from the lamp is reduced in intensity on passing through P alone. But now rotating P has a dramatic effect on the light coming from P . In one position, the intensity transmitted by P followed by P is nearly zero. When turned by 90Β° from this position, P transmits nearly the full intensity emerging from P (Fig. 10.18).
Detailed Explanation
This section introduces Malus' Law, which describes how the intensity of transmitted light changes as it passes through polaroids. When unpolarised light passes through a single polaroid, its intensity is halved. If a second polaroid is placed at an angle to the first, the transmitted intensity depends on the angle between their axes. Malus' Law quantitatively describes this relationship, explaining how the light's intensity is affected depending on their relative position.
Examples & Analogies
Consider two window blinds β one is horizontal, and the other is vertical. If you look through the first blind (which lets light in), you'll see plenty of light. But when you put the second blind in front at a right angle, it blocks much of that light. If you tilt the second blind to allow some light through (up to a certain angle), you can control how much light you let into the room, illustrating Malus' Law.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Polarisation: Orientation of oscillations in waves.
-
Polaroid: Material filtering light based on orientation.
-
Linearly Polarized Light: Light oscillating in one direction.
-
Malus's Law: Relationship between intensity and angle in polarizers.
-
Unpolarized Light: Light oscillating in multiple directions.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Sunglasses reduce glare by blocking polarized light from surfaces.
-
Photographic filters enhance image quality by controlling light polarity.
-
LCD screens utilize polarized light for display clarity.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
Polaroids can help you see, / Block that glare, it's clear as can be!
π Fascinating Stories
-
Imagine walking on a sunny beach. You squint because of the glare from the waves, but wearing polarized sunglasses makes you see the colors vividly without the harsh glare.
π§ Other Memory Gems
-
To remember the effect of angle: 'As the angle swings, the brightness clings.'
π― Super Acronyms
P.E.A.R. = Polarized Electric Amplitude Result, to remember how electric fields work.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Polarisation
Definition:
The orientation of oscillations perpendicular to the direction of wave propagation.
-
Term: Polaroid
Definition:
A material that filters light waves based on their orientation, allowing only certain directions of light to pass through.
-
Term: Linearly Polarized Light
Definition:
Light waves in which the electric field oscillates in a single direction.
-
Term: Malus's Law
Definition:
A law that states the intensity of polarized light after passing through a polarizer is proportional to the cosine square of the angle between the light's electric field and the polarizer's pass axis.
-
Term: Unpolarized Light
Definition:
Light that has electric field vectors oscillating in multiple random directions.