Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Wave Reflection
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we will be discussing how reflections occur when a plane wave interacts with a reflective surface. Can anyone tell me what Huygens' principle is?
It states that each point on a wavefront is a source of secondary waves.
Exactly! Now, when a plane wave meets a reflecting surface, we can use Huygens' principle to analyze the reflection. What do you think happens to the wavefront?
Does it change direction?
Correct! The wavefront reverses direction. We can visualize this by imagining that the wavefront AB collides with surface MN. From point A, we draw a sphere to represent the wave's front. What can we conclude about the angle at which it strikes the surface?
I think that's the angle of incidence!
Great! And what can we say about the angle of reflection in relation to that?
It should be equal, right?
Exactly! This leads us to the law of reflection: the angle of incidence equals the angle of reflection. This understanding is vital when analyzing how lenses and mirrors operate.
Constructing Reflected Wavefronts
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we've established the law of reflection, let's see how to construct the reflected wavefront using Huygens' principle. When the plane wave AB strikes surface MN, we represent incident wavefront using the distance covered from point B to point C.
How do we construct the reflected wavefront?
We draw a sphere of radius vt from point A, where v is the wave's speed, and t is the time taken. The tangent plane CE drawn from point C represents the reflected wavefront. Why do you think we need this approach?
To visualize how the wavefront changes after reflection?
Exactly! It helps us understand the geometry of wave behavior. If we analyze triangles formed, we can see that angles i and r must be equal due to congruence. Can anyone summarize the implications of this reflected wavefront construction?
It confirms the consistency of the laws we've established so far, and it will help us to understand more complex optical phenomena!
Excellent observation! This foundational understanding is crucial for deeper studies in wave optics.
Practical Applications of Reflection
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we know how plane waves reflect, let's connect this to practical applications in optics. Can anyone give me examples of devices that use reflection?
Mirrors!
And lenses too, right?
Absolutely! Mirrors utilize reflection to redirect light. When light hits a mirror, the principles we discussed dictate how it reflects and can focus or project an image. For lenses, even though they primarily refract light, the behavior of reflection plays a crucial role in their design.
How does understanding these concepts help us with designing better optical instruments?
Great question! A solid grasp of reflection allows engineers to innovate optics for better focusing, image clarity, and efficiency in devices like telescopes and cameras. Any last thoughts before we wrap up?
I think understanding angles and behaviors of light can also help us in photography!
Exactly! Light behavior impacts many fields. Remember, the angle of incidence equals the angle of reflection is your key takeaway!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section details how the reflection of a plane wave at a surface can be understood through Huygensβ principle, leading to the conclusion that the angle of incidence is equal to the angle of reflection. It emphasizes the method of constructing reflected wavefronts using spherical wavelets.
Detailed
Reflection of a Plane Wave by a Plane Surface
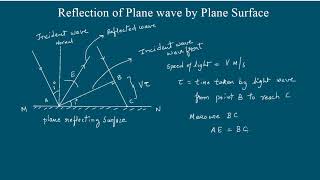
This section focuses on the behavior of a plane wave when it encounters a reflecting surface, illustrated through the use of Huygens' principle. When a plane wave, represented by wavefront AB, strikes a reflecting surface MN at an angle of incidence i, the speed of the wave in the medium and the time taken for the wave to travel form the foundation of analysis. The wavefront's advancement can be visualized by constructing a sphere from point A of the plane wave, with radius vt (where v is the speed of the wave and t is the time taken to reach point C).
As the sphere reflects, it's understood that the reflected wavefront CE is tangent to the sphere at point C. Analyzing the triangles formed, it becomes apparent that the angles of incidence (i) and reflection (r) are congruent, thus confirming the law of reflection:
Angle of incidence equals angle of reflection (i = r).
Understanding this reflection phenomenon enables a deeper comprehension of optical devicesβlike lenses and mirrorsβpreviously covered in geometrical optics. The section effectively links Huygensβ principle to practical applications in optics, setting the stage for further explorations in wave behavior.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Incident Plane Wave and Reflection Setup
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We next consider a plane wave AB incident at an angle i on a reflecting surface MN. If v represents the speed of the wave in the medium and if t represents the time taken by the wavefront to advance from the point B to C then the distance BC = vt.
Detailed Explanation
In this section, we discuss how a plane wave behaves when it strikes a flat surface at an angle. We denote the incident wave as AB and the angle at which it meets the surface as 'i'. The wave moves in a medium where its speed is 'v', and we define 't' as the time taken for the wavefront to travel a specific distance. Here BC is the distance that the wavefront travels during that time, calculated by multiplying speed 'v' by time 't'.
Examples & Analogies
Imagine throwing a pebble on the surface of a still pond. The resulting waves move outward. Now, if the edge of the pond represents a flat surface where the pebble's waves encounter, the manner in which these waves reflect back illustrates the wave's behavior upon hitting a reflecting surface.
Constructing the Reflected Wavefront
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In order to construct the reflected wavefront we draw a sphere of radius vt from the point A as shown in Fig. 10.6. Let CE represent the tangent plane drawn from the point C to this sphere. Obviously AE = BC = vt.
Detailed Explanation
To visualize the reflected wavefront, we create a sphere originating from point A with a radius equal to the distance BC, which is vt. CE is the tangent drawn from point C to the surface of the sphere, which represents the new wavefront after reflection. This means that the distance AE, which is the distance in the reflected medium, equals the distance BC, maintaining consistency due to the principles of wave movement.
Examples & Analogies
Think of a basketball bouncing off a flat wooden floor. When the ball strikes the floor, it compresses slightly (like the wave sphere) and then rebounds in a new direction, following a clear trajectory. Just as the basketball's reflection depends on its angle of incidence, the wave reflects off surfaces depending on predictable geometric principles.
Law of Reflection
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If we now consider the triangles EAC and BAC we will find that they are congruent and therefore, the angles i and r (as shown in Fig. 10.6) would be equal. This is the law of reflection.
Detailed Explanation
Upon analyzing the triangles formed by the incident and reflected wavefronts (EAC and BAC), it is evident that these triangles are congruent, meaning they have the same shape and size. Consequently, the angles formed by the incident wave (i) and the reflected wave (r) are equal. This principle is known as the law of reflection, which states that the angle of incidence is equal to the angle of reflection.
Examples & Analogies
Consider looking into a calm lake. The angle at which your image appears in the water (the angle of incidence) is precisely mirrored in the reflection seen in the water (angle of reflection). This everyday experience of observing reflections in water exemplifies the law of reflection in action.
Understanding Wavefront Behavior with Optics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Once we have the laws of reflection and refraction, the behaviour of prisms, lenses, and mirrors can be understood.
Detailed Explanation
The laws of reflection and refraction provide foundational knowledge for understanding how light interacts with different optical devices like prisms, lenses, and mirrors. Once we comprehend these laws, we can predict how light waves will behave as they strike and pass through these devices, influencing their paths and behaviors in various applications.
Examples & Analogies
Think of a pair of glasses. When light enters the lenses, it bends (refraction) and reflects (reflection) according to these laws, allowing you to see more clearly. This practical use of optics - using laws of reflection and refraction - underscores the importance of understanding wavefront behavior for real-world applications.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Wavefront: A surface over which an oscillating wave has a constant phase.
-
Huygens' Principle: Every point on a wavefront can be considered a source of secondary waves.
-
Law of Reflection: The angle of incidence is equal to the angle of reflection.
-
Reflective Surface: A surface that reflects waves rather than transmitting them.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A plane wave of light reflecting off a flat mirror demonstrates the law of reflection.
-
Using Huygens' principle, one can model how a flashlight beam reflects off a shiny surface.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
When a wave meets the plane, reflections occur, with angles the same, youβll surely concur.
π Fascinating Stories
-
Imagine walking on a beach, where waves ripple and reflect off the shore, just as light bounces back at the same angle it hits the sand.
π§ Other Memory Gems
-
I = R for light to see: Incidence equals Reflectionβremember, that's the key!
π― Super Acronyms
WAVE
- Wavefronts Always Verify Equality (of incidence and reflection angles).
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Huygens' Principle
Definition:
A principle that states every point on a wavefront serves as the source of secondary waves and the new wavefront is the envelope of these secondary waves.
-
Term: Angle of Incidence
Definition:
The angle between the incident wavefront and the normal to the surface at the point of incidence.
-
Term: Angle of Reflection
Definition:
The angle between the reflected wavefront and the normal to the surface at the point of reflection.
-
Term: Wavefront
Definition:
A surface over which an oscillating wave has a constant phase.
-
Term: Plane Wave
Definition:
A wave with wavefronts that are infinite and parallel planes.
-
Term: Reflective Surface
Definition:
A surface that reflects light rather than transmitting it.