Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Damped MDOF Systems
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today we are diving into the equations of motion for damped MDOF systems. Can anyone share what they understand by damping in a system?
Isn't damping a way to reduce vibrations?
Exactly! Damping refers to methods that dissipate energy, preventing oscillations from continuing indefinitely. In MDOF systems, we express damping through a damping matrix, [C].
What does the damping matrix include?
Great question! It describes how damping affects each degree of freedom in the system. When is damping considered classical or proportional?
I think it's when the damping is related to mass and stiffness, right?
Correct! When we have classical damping, it can be represented as [C]=α[M]+β[K]. Let’s remember that classical damping helps maintain the decoupled form of the equations.
Why is it important that the equations remain uncoupled?
Excellent query! Uncoupled equations allow us to solve each modal equation independently, much like we do in damped SDOF systems.
To summarize, today we learned about the role of the damping matrix in MDOF systems, the definition of classical damping, and the significance of uncoupling equations for easier solutions.
Understanding the Modal Damping Ratio
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's explore the modal damping ratio, ζ. Why do you think it's significant in vibrational analysis?
It probably helps in determining how much energy is lost during each cycle of vibration.
Exactly! The damping ratio is crucial for assessing how quickly a system returns to its rest position after a disturbance. Can someone tell me the form of the equations we observe for damped MDOF systems?
Is it q¨(t)+2ζ ω q˙(t)+ω² q(t)=0 for each mode?
Spot on! This resembles the damped SDOF system equations, allowing for a seamless understanding of dynamics in various modes.
So, if we understand the single degree of freedom case, it applies here too?
That's correct! Recognizing this relationship simplifies our learning and analysis. Let’s summarize: The modal damping ratio plays a key role in energy dissipation in damped MDOF systems, with equations paralleling those in SDOF systems.
Applications of Damped MDOF Equations
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let’s discuss applications of the damped MDOF equations in engineering. Why are these equations relevant in seismic design?
They help predict how structures respond to earthquakes?
Correct again! By modeling structures with these equations, engineers can ensure safety during seismic activities. Which factors do you think affect the performance of a building during an earthquake?
I guess the damping ratios and the natural frequencies?
Absolutely! The damping ratio significantly influences how structures dissipate energy. Just as a reminder, we use modal analysis based on these equations to assess seismic responses.
So this impacts both the design and the maintenance of structures?
You got it! Understanding how MDOF systems behave under dynamic loads helps with risk management and structural integrity considerations. To conclude, the equations of motion for damped MDOF systems are fundamental for ensuring resilient engineering practices in seismic design.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section details the formulation of equations of motion in the presence of damping in MDOF systems, particularly when classical (proportional) damping is assumed. It explains how the equations for damped MDOF systems can maintain uncoupled modal equations similar to damped Single Degree of Freedom (SDOF) systems, as well as the significance of the damping ratio.
Detailed
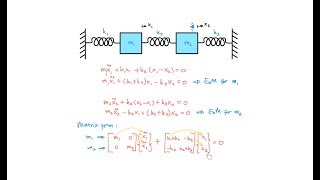
In MDOF systems with damping, the equations of motion can be expressed as
[M]{u¨}+[C]{u˙}+[K]{u}={0}, where [C] represents the damping matrix. If the damping is classical (proportional), given by [C]=α[M]+β[K], the equations remain uncoupled, forming a familiar second-order differential equation of the form q¨(t)+2ζ ω q˙(t)+ω² q(t)=0 for each mode. Here, ζ represents the modal damping ratio. This connection to damped SDOF systems allows engineers to leverage existing solutions and analyses. Understanding the behavior of damped MDOF systems is crucial for accurately modeling dynamic responses, particularly under seismic loading conditions.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
General Formulation with Damping
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When damping is present:
[M]{u¨}+[C]{u˙}+[K]{u}={0}
- [C]: Damping matrix
Detailed Explanation
In this chunk, we discuss the general equation of motion for a damped multiple degree of freedom (MDOF) system. When we consider damping, we add a damping matrix [C] to our equations of motion. This changes the format of the equation to include terms from both the mass matrix [M] and the stiffness matrix [K], along with the velocity vector {u˙}. The presence of the damping matrix [C] accounts for the energy dissipation in the system, which is crucial for realistic modeling of vibrating structures under real-world conditions.
Examples & Analogies
Think of driving a car over a bumpy road. The suspensions of the car act like dampers; they absorb the bumps and vibrations, preventing the car from bouncing too much. Similarly, in engineering structures, damping helps minimize excessive vibrations caused by events like earthquakes.
Classical Damping Structure
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If damping is classical (proportional), i.e., [C]=α[M]+β[K], then the modal equations remain uncoupled:
q¨ (t)+2ζ ω q˙ (t)+ω2q(t)=0
Where:
- ζ : Modal damping ratio
Detailed Explanation
This chunk explains a specific case of damping called classical or proportional damping. In this scenario, the damping matrix [C] can be expressed as a combination of the mass matrix [M] and stiffness matrix [K]. Using this relationship allows us to further simplify the modal equations of motion. The resulting differential equations are similar to those for damped single degree of freedom (SDOF) systems, making it easier to analyze each mode independently. The term ‘modal damping ratio’ (ζ) quantifies how much damping is present in relation to the system's natural frequency.
Examples & Analogies
Imagine a swing. When you push it, it swings back and forth until it gradually stops due to air resistance (damping). If you adjust how strong the push is (analogous to controlling the damping), you can tune the swing's motion to be smooth and steady, just like how engineers adjust damping in buildings to maintain stability during winds or earthquakes.
Equivalence to Damped SDOF Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
These equations are identical to damped SDOF systems.
Detailed Explanation
In this chunk, we emphasize that when using classical damping, the equations derived for the modal responses of MDOF systems mirror those of damped single degree of freedom systems. This is important because it means that the analysis methods developed for SDOF systems can be applied directly to MDOF systems as well. This equivalence simplifies the mathematical treatment of MDOF systems and exploits the computational tools and methods already available for SDOF analysis.
Examples & Analogies
Consider a violin string that vibrates when plucked. Whether it vibrates in a simple or complex manner, the fundamental principles governing its relaxation and sound production remain the same. Similarly, regardless of the complexity of a structure (like a tall building), the principles of damping apply equally, making them manageable using established methods.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Damping Matrix: Represents energy dissipation in a system.
-
Classical Damping: Damping proportional to mass and stiffness affects the system response.
-
Modal Damping Ratio: Affects the decay rate of vibrations in oscillatory systems.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A building during an earthquake behaves like a damped MDOF system, where the damping matrix mitigates extreme oscillations.
-
Bridges designed with damping systems can exhibit controlled motion to withstand varying loads, especially during seismic events.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Damping is a vital plan, it helps our buildings stand. Without this steady hand, they'd wobble 'til they're banned!
📖 Fascinating Stories
-
Imagine a tall tower swaying in the wind. As it bends, the damping system within helps it relax and return to straight, preventing catastrophic failure during storms.
🧠 Other Memory Gems
-
DAMP: Damping Affects Modal Performance - a reminder of how damping influences vibrational responses.
🎯 Super Acronyms
MDOF
- Multiple Degrees of Freedom
- indicating systems that vibrate in various modes due to loads.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Damping Matrix [C]
Definition:
A matrix representing the damping effects within a dynamic system.
-
Term: Classical Damping
Definition:
A form of damping where the damping matrix is proportional to both the mass and stiffness matrices.
-
Term: Modal Damping Ratio (ζ)
Definition:
A dimensionless measure describing the damping of a system, important for determining the rate of oscillation decay.