Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Mode Shape Normalization
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we are diving into the normalization of mode shapes. Can anyone tell me why we might want to normalize mode shapes in our analysis?
Maybe to simplify the calculations?
Exactly! Normalization simplifies computations. We do two types of normalization, mass normalization and stiffness normalization. Let’s discuss what those mean. Who can remind us what mass normalization is?
I think it involves setting the sum of the mode shape weighted by mass to one?
Correct, it's represented as {ϕ}T [M]{ϕ} = 1! This allows us to compare different modes more easily. Now, why might we also want stiffness normalization?
To ensure that the stiffness is also proportional in our calculations?
Right on! Stiffness normalization has the same formula but focuses on the stiffness matrix. Both methods help in modal superposition, which is crucial for analyzing MDOF systems.
Details on Mass Normalization and Its Importance
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
So, let’s talk specifically about mass normalization. What do you think happens if we fail to normalize our mode shapes?
The results could be misleading, right? They wouldn't accurately represent the distribution of mass.
Exactly! If our mode shapes aren't normalized, we risk inaccurate results in our simulations of behavior during seismic events. Does anyone remember the formula for mass normalization?
{ϕ}T [M]{ϕ} = 1!
Correct! This relationship is pivotal to ensuring that each mode shape contributes correctly to the system's dynamic response.
So mass normalization is crucial for dynamic behavior analysis?
Yes! It makes it possible to interpret modal responses effectively, especially in seismic analysis.
Exploring Stiffness Normalization
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let’s shift our focus to stiffness normalization. Why is this method also necessary?
It helps ensure that our stiffness values are accurately represented, right?
Yes! The equation is {ϕ}T [K]{ϕ} = 1. This normalization secures dimensional consistency, ensuring our calculations stay relevant across various load cases. Can anyone think of a scenario where stiffness normalization could be particularly useful?
During an earthquake, where different stiffness levels could drastically change how a structure behaves.
Exactly! Understanding the relationship between our mode shapes and stiffness helps predict behavior under such dynamic conditions.
Combining Normalization Methods
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we’ve covered both methods, how do you think they integrate during modal analysis?
I think using both ensures that we have a comprehensive analysis of our structure under all conditions.
That's right! By combining both normalization approaches, we achieve a more accurate representation of dynamic interactions within MDOF systems.
So we can effectively model seismic responses!
Exactly! And that is critical for ensuring the integrity and safety of structures in real-world applications.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
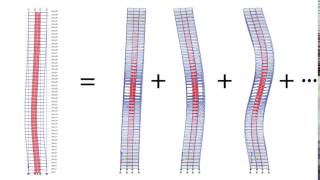
In this section, normalization of mode shapes is discussed, focusing on two common methods: mass normalization and stiffness normalization. These methods are essential for modal superposition and simplifying computations in the modal analysis of multiple degree of freedom systems.
Detailed
Normalization of Mode Shapes
Normalization of mode shapes is a critical step in the analysis of Multiple Degree of Freedom (MDOF) systems, facilitating clearer interpretations and simplifications in computational procedures. There are two predominant normalization methods discussed:
-
Mass Normalization:
This method sets the condition that the mass-weighted sum of the mode shape is equal to 1, represented mathematically as:
$$\{ϕ\}^{T} [M] \{ϕ\} = 1.$$
This ensures that the mode shapes are not only accurately represented but also proportional to the system's mass distribution. -
Stiffness Normalization:
In contrast, stiffness normalization demands that the stiffness-weighted sum of the mode shape equals 1, expressed as:
$$\{ϕ\}^{T} [K] \{ϕ\} = 1.$$
This approach also aids in maintaining dimensional consistency when analyzing structural responses under various loading scenarios.
Normalization plays a vital role in modal superposition techniques and is crucial for effective computation in dynamic analysis processes, making it a fundamental concept for engineering applications in seismic analysis and design.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Normalization Methods
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Mode shapes can be normalized in two common ways:
- Mass normalization:
{ϕ }T [M]{ϕ }=1
i i
- Stiffness normalization:
{ϕ }T [K]{ϕ }=1
i i
Detailed Explanation
Normalization of mode shapes is important in the analysis of dynamic systems, especially in modal analysis. There are two primary methods to normalize mode shapes:
1. Mass Normalization: This method sets the inner product of the mode shape vector with respect to the mass matrix equal to one. In mathematical terms, it looks like this: {ϕ }T [M]{ϕ } = 1. This means when you take the mode shape and multiply it by the mass matrix, the result is 1.
- Stiffness Normalization: Similar to mass normalization, but this time you use the stiffness matrix. Here, the equation {ϕ }T [K]{ϕ } = 1 signifies that the internal forces due to the stiffness of the system align correctly with the mode shape.
These normalizations ensure that the mode shapes have a standard scale, which makes calculations involving modal superposition simpler.
Examples & Analogies
Think of normalizing mode shapes like ensuring everyone in a dance troupe performs to a consistent beat. If each dancer has their own tempo (like unnormalized modes), it makes synchronizing the performance challenging. But once all dancers adjust to the same rhythm (normalization), they can move together harmoniously, making the performance more impactful.
Importance of Normalization
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Normalization is useful for modal superposition and simplification in computations.
Detailed Explanation
The process of normalization plays a pivotal role in simplifying complex calculations in structural dynamics. Once modes are normalized, they can easily be combined using modal superposition. This approach allows engineers to predict how structures react under various loads by adding the effects of each mode.
When conducting modal analysis, having normalized modes ensures that the contributions from each mode to the overall system response can be calculated without confusion arising from varying scales of the mode shapes. This results in clearer and more accurate computational models of dynamic behavior in structures.
Examples & Analogies
Consider trying to lift weights at the gym. If one weight is measured in kilograms and another in pounds, it can be tricky to determine how much total weight you're lifting. Once you convert all weights to the same unit (normalization), it's easy to add them up and understand your total effort. Similarly, normalizing mode shapes gives us a standard way to combine their effects on a structure.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Mass Normalization: Ensures that the mass-weighted sum of the mode shape equals one.
-
Stiffness Normalization: Ensures that the stiffness-weighted sum of the mode shape equals one.
-
Importance of Normalization: Reduces computational errors and enhances the accuracy of modal analyses.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of mass normalization might include setting up a multi-storey building model and ensuring that the mode shape reflects the distribution of mass across the floors.
-
In stiffness normalization, adjusting mode shapes for a bridge model ensures that the natural frequencies calculated incorporate the stiffness provided by different spans.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When mass and stiffness weigh in sync, the shapes will link; normalization's the key to prevent our minds from going pink.
📖 Fascinating Stories
-
Imagine an architect named Sam, who builds a tower with great jam. One day he forgot to normalize what he had, and the structure just turned out so bad!
🧠 Other Memory Gems
-
Remember 'M and S' for 'Mass' and 'Stiffness'; both must equal one for computations to be bliss!
🎯 Super Acronyms
M.N. = Mass Normalization; S.N. = Stiffness Normalization is the foundation of our simulation.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Mode Shape
Definition:
A distinct pattern of motion that a structure undergoes when vibrating at a particular natural frequency.
-
Term: Normalization
Definition:
The process of adjusting mode shapes so that their values conform to a standard, helping in analysis.
-
Term: Mass Normalization
Definition:
A method of normalizing mode shapes by setting the mass-weighted sum of the mode shape equal to one.
-
Term: Stiffness Normalization
Definition:
A method of normalizing mode shapes by setting the stiffness-weighted sum of the mode shape equal to one.
-
Term: Modal Analysis
Definition:
A procedure to determine the natural frequencies and mode shapes of a system.