Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to MDOF System
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we will begin by discussing the concept of Multiple Degrees of Freedom systems, also known as MDOF systems. Can anyone tell me what distinguishes these from Single Degree of Freedom systems?
I think MDOF systems have more than one mass and can vibrate in multiple modes.
Exactly! MDOF systems require multiple independent coordinates to fully describe their motion. This leads us to their governing equations. The motion of an n-DOF linear system can be described by equations involving mass and stiffness matrices.
What are those matrices?
Great question! The mass matrix [M] and the stiffness matrix [K] contain the mass and stiffness properties of the system, respectively. They are crucial for deriving the movement equations.
Are those matrices always diagonal?
In lumped mass systems, yes, the mass matrix is usually diagonal. This indicates that each degree of freedom is independent of others. As we progress, we will delve deeper into these concepts.
To summarize, MDOF systems require multiple coordinates for their motion, and their equations of motion are determined by mass and stiffness matrices.
Equations of Motion
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now let's look at the main equation governing undamped MDOF systems. The general form is given as [M]{u¨(t)} + [K]{u(t)} = {0}. Can anyone explain what this represents?
It shows the relationship between acceleration and displacement in the system.
Correct! This equation indicates that the system's mass times acceleration plus the stiffness times displacement must equal zero, highlighting the balance of forces acting on the system.
What does it mean when there are no external forces in this equation?
Good observation! When there are no external forces, the system is considered 'undamped'. It allows us to focus on the inherent dynamics without outside interference.
To wrap up, the governing equation helps us understand the interrelationship of acceleration, stiffness, and mass within the system.
Mass and Stiffness Matrix Properties
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let's delve into the properties of the mass and stiffness matrices. Who can tell me about the nature of the mass matrix in lumped systems?
It is usually diagonal, meaning that there's no coupling between the different degrees of freedom.
Exactly! And how about the stiffness matrix?
I think it is symmetric and positive-definite.
Right again! This symmetry and positive definiteness ensure that the solutions will be stable. Do you all understand why these properties are essential in deriving the equations of motion?
So, it’s about ensuring that the physical behavior reflects that of real systems, correct?
Exactly! These properties are vital for deriving a system of n coupled second-order differential equations, which are crucial for analyzing the dynamic behavior of structures.
In summary, the mass and stiffness matrices play an essential role in modeling undamped MDOF systems' dynamics.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we delve into the equations of motion governing undamped MDOF systems, represented by coupled second-order differential equations. The mass and stiffness matrices play a vital role in defining the system's dynamics, leading to a general form that captures the motion of these systems without external forces.
Detailed
Detailed Summary
In this section, we consider the dynamics of an n-degree of freedom (DOF) linear system characterized by lumped masses and linear springs. The fundamental equation governing undamped MDOF systems is given by:
\[ [M]{u¨(t)} + [K]{u(t)} = {0} \]
Where:
- [M] is the mass matrix, which is typically diagonal in lumped mass systems, indicating that each degree of freedom has associated mass.
- [K] is the stiffness matrix, which is symmetric and positive-definite.
- {u(t)} represents the displacement vector, while {u¨(t)} denotes the acceleration vector.
This equation leads to a system of n coupled second-order differential equations, reflecting the motion of multiple interconnected masses and springs. Understanding these equations is crucial for analyzing the dynamic behavior of structures under various conditions, particularly in the context of seismic loads. The properties of the mass matrix and stiffness matrix are significant as they influence the overall response of the structure.
Youtube Videos
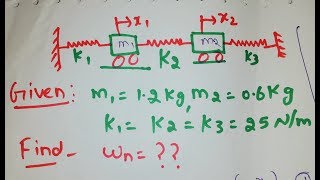
Audio Book
Dive deep into the subject with an immersive audiobook experience.
General Form of Equations of Motion
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Consider an n-DOF linear system with lumped masses and linear springs. The general form of the equations of motion without damping and external forces is:
[M]{u¨(t)}+[K]{u(t)}={0}
Detailed Explanation
In this chunk, we introduce an n-degree-of-freedom (n-DOF) linear system, which means that the system can move in n different independent directions. The equation describes how this system behaves when it is either stationary or in motion. The equation itself is comprised of three components:
1. [M]{u¨(t)} refers to the mass matrix multiplied by the acceleration vector. This part describes how the mass of the system resists changes in motion (inertia).
2. [K]{u(t)} refers to the stiffness matrix multiplied by the displacement vector. This part describes how the system reacts when it is displaced from its equilibrium position (elastic force).
3. The equation is set equal to zero, indicating that, in the absence of external forces or damping, the internal forces balance each other out.
Examples & Analogies
You can think of this system like a multi-story building swaying in the wind during a storm. Each floor (or mass) moves independently but is also connected through springs (stiffness). The forces acting on each floor are similar to how the balance of forces keeps everything stable, like a well-designed structure that does not topple over in strong winds.
Mass and Stiffness Matrices
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Where:
- [M] = Mass matrix (n×n)
- [K] = Stiffness matrix (n×n)
- {u(t)} = Displacement vector
- {u¨(t)} = Acceleration vector
Detailed Explanation
Here we define the matrices involved in our equations. The mass matrix [M] captures the distribution of mass across the system. In many practical systems, this matrix is diagonal, meaning each mass primarily affects itself and has minimal interaction with others. The stiffness matrix [K] represents how the structure's components resist deformation. Importantly, it is symmetric and positive-definite, which ensures stable behavior in dynamic analysis. The displacement and acceleration vectors {u(t)} and {u¨(t)} include all the displacements and accelerations of the n masses in our system, respectively.
Examples & Analogies
Imagine a set of building blocks where each block has a different weight (mass) and is connected by rubber bands (stiffness). The way these blocks would move when you pull or compress the rubber bands corresponds to how the mass and stiffness matrices interact in the motion equations.
Coupled Differential Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Key Concepts:
- Mass matrix is usually diagonal in lumped-mass systems.
- Stiffness matrix is symmetric and positive-definite.
- This leads to a system of n coupled second-order differential equations.
Detailed Explanation
In this section, we emphasize the key characteristics of our matrices. A diagonal mass matrix indicates that the forces acting on each mass are primarily independent, simplifying calculations. The symmetry and positive-definiteness of the stiffness matrix ensure that the system's response is well-behaved. The resulting set of equations forms n coupled second-order differential equations, which can be solved to reveal the dynamic behavior of the system over time. Coupling means that changes in one mass's position will affect the others, showcasing the interconnected nature of an MDOF system.
Examples & Analogies
Consider a set of interlinked springs where changing one spring's tension directly impacts the others' tension. The movement of each spring influences its neighbors, much like how the coupled equations represent interactions among different masses in the MDOF system.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Equations of Motion: The primary equation of motion for MDOF systems relates the mass and stiffness matrices to the system's dynamic behavior.
-
Coupled Differential Equations: Understanding that the dynamics of MDOF systems are governed by a set of coupled second-order differential equations.
-
Mass and Stiffness Properties: The mass matrix is typically diagonal, while the stiffness matrix is symmetric and positive-definite, which are essential properties for stability.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
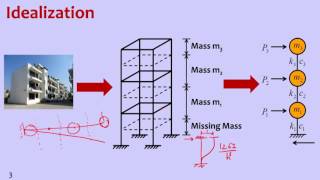
Consider a three-story building represented as an MDOF system with three lumped masses located at each floor, linked by stiffness springs. The movement of this building under seismic forces can be analyzed using the derived equations of motion.
-
In a suspension bridge, the cables and road deck can be modeled as an MDOF system, where the number of degrees of freedom corresponds to the various sections that can move independently.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Mass is diagonal, stiffness does shine, in MDOF systems, dynamics align.
📖 Fascinating Stories
-
Once in a city, tall buildings swayed, their masses hung heavy, and springs often played. The architects knew, with equations in hand, they'd model the dance, the sway, and the stand.
🧠 Other Memory Gems
-
MDS – Mass, Dynamics, and Stiffness are key for MDOF.
🎯 Super Acronyms
MDOF stands for 'Multiple Degrees of Freedom', reminding us that more is often lively!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Multiple Degree of Freedom (MDOF)
Definition:
A mechanical or structural system that requires two or more independent coordinates to describe its motion.
-
Term: Mass Matrix [M]
Definition:
A matrix that represents the mass distribution of the system; usually diagonal in lumped-mass systems.
-
Term: Stiffness Matrix [K]
Definition:
A symmetric and positive-definite matrix that captures the stiffness characteristics of the system.
-
Term: Displacement Vector {u(t)}
Definition:
A vector that represents the positions of the system's elements over time.
-
Term: Acceleration Vector {u¨(t)}
Definition:
A vector representing the accelerations of the corresponding displacements over time.