Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Mode Shapes
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're going to discuss the concept of mode shapes in MDOF systems. Can anyone tell me what mode shapes represent in this context?
Mode shapes show how a structure deforms during vibration.
Exactly! They are the shapes that the structure assumes at its natural frequencies. Now, what do you think happens when we analyze two different mode shapes?
They might overlap or interfere with each other?
Good thought! However, in our analysis, we find that distinct mode shapes are orthogonal. Can you recall what orthogonality means?
It means they are perpendicular or independent in some sense.
That's correct! We'll explore this concept in more detail, focusing on mass and stiffness orthogonality.
Mass and Stiffness Orthogonality
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's consider the two orthogonality properties: mass orthogonality and stiffness orthogonality. Can someone recall the mathematical expression for mass orthogonality?
It’s {\phi_i}^T [M] {\phi_j} = 0 for i ≠ j.
Excellent! This means that for two different mode shapes, their mass contributions do not interfere with each other. Why do you think this is significant?
It likely helps in simplifying the equations of motion.
Exactly! Now, how about stiffness orthogonality? Can someone give me that expression?
It's {\phi_i}^T [K] {\phi_j} = 0 for i ≠ j.
Right! These properties are crucial for decoupling the equations of motion in MDOF systems.
Applications of Orthogonality in Analysis
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we understand these concepts, can anyone explain how these orthogonality properties help in analyzing MDOF systems?
They allow us to break down complex equations into simpler ones!
Correct! By using orthogonality, we can derive equations that are simpler to solve independently. Can you outline what that means for engineers?
It means we can focus on one mode at a time without worrying about the others.
Absolutely! This makes analysis much more manageable, especially when dealing with dynamic loads such as earthquakes.
So, each mode is like a separate puzzle we can solve individually?
Precisely! Great analogy! In summary, the orthogonality helps us effectively analyze MDOF systems and predict their behavior under various conditions.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The orthogonality of mode shapes is a critical aspect of modal analysis in MDOF systems, where the eigenvectors exhibit mass and stiffness orthogonality. These properties allow the decoupling of equations of motion, streamlining the analysis of such systems.
Detailed
Orthogonality of Mode Shapes
In multiple degree of freedom (MDOF) systems, the mode shapes or eigenvectors possess unique orthogonality properties. Specifically, these vectors are orthogonal with respect to both the mass matrix [M] and the stiffness matrix [K]. The key properties include:
- Mass Orthogonality:
$$ {\phi_i}^T [M] {\phi_j} = 0 \quad \text{for} \quad i \neq j $$
This states that the inner product of distinct mode shapes with respect to the mass matrix results in zero, indicating that their contributions do not overlap.
- Stiffness Orthogonality:
$$ {\phi_i}^T [K] {\phi_j} = 0 \quad \text{for} \quad i \neq j $$
Similar to mass orthogonality, this property confirms that the eigenvectors remain orthogonal when considered in the context of the stiffness matrix.
These orthogonality properties are essential for simplifying the analysis of MDOF systems, particularly in decoupling the equations of motion. By utilizing these properties, it becomes feasible to express the system's behavior using independent modal equations, thus enabling easier computation of responses under dynamic loading.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Mass Orthogonality
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The eigenvectors (mode shapes) satisfy orthogonality properties:
1. Mass Orthogonality:
{ϕ }T [M]{ϕ }=0 for i ≠ j
Detailed Explanation
Mass orthogonality means that the inner product of any two mode shapes, when weighted by the mass matrix, results in zero if they are different modes. In mathematical terms, this is expressed as {ϕ }T [M]{ϕ }=0 for i ≠ j. This property is crucial because it indicates that different modes do not influence each other in terms of their mass distribution. Therefore, we can analyze each mode independently when solving the equations of motion.
Examples & Analogies
Imagine a dance floor with two dancers. If they are dancing to different rhythms (each representing a mode), they can move freely without interfering with each other's movements. Their dance styles do not overlap, just as the mode shapes do not affect each other in mass orthogonality.
Stiffness Orthogonality
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Stiffness Orthogonality:
{ϕ }T [K]{ϕ }=0 for i ≠ j
Detailed Explanation
Stiffness orthogonality indicates that different mode shapes are also orthogonal with respect to the stiffness matrix, meaning their inner product weighted by the stiffness matrix is zero for distinct modes ({ϕ }T [K]{ϕ }=0 for i ≠ j). This implies that each mode shape can be analyzed separately when considering the system’s response to stiffness forces, further simplifying the analysis of the structure.
Examples & Analogies
Consider two springs with different attachments (each representing a different mode). If you stretch one spring, it will not affect the other spring's ability to stretch independently, similar to the concept of stiffness orthogonality where each mode does not affect the stiffness of another.
Importance of Orthogonality Properties
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
These properties are used to decouple the equations of motion and simplify analysis.
Detailed Explanation
The orthogonality properties of mode shapes are significant because they allow us to decouple the equations of motion of the system into simpler, independent equations. This decoupling means that instead of analyzing a complicated system of equations all together, we can treat each mode independently. This simplification makes solving the dynamic response of MDOF systems much easier and more efficient.
Examples & Analogies
Think about solving a complex puzzle. If you could separate the puzzle pieces into distinct sections based on their colors, it would be easier to solve each section one at a time rather than handling all the pieces together. Similarly, the orthogonality of mode shapes allows us to solve dynamic problems in isolation.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Mass Orthogonality: Refers to the property that distinct mode shapes are orthogonal with respect to the mass matrix.
-
Stiffness Orthogonality: Indicates that distinct mode shapes are orthogonal with respect to the stiffness matrix.
-
Decoupling of Equations: The process by which equations of motion can be simplified due to the orthogonality of mode shapes.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
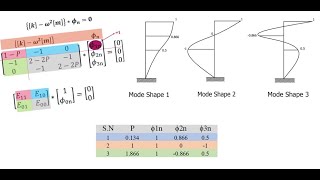
In a two-story shear building model, the first mode shape may represent lateral movement while the second represents twisting. These shapes can be analyzed independently due to their orthogonality.
-
When computing the natural frequencies of a three-story building, the equations derived are simplified because the contributions from each mode shape do not interfere with one another.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Orthogonal means no overlap, like dancers in a coordinated clap.
📖 Fascinating Stories
-
Imagine a dance floor with multiple couples dancing without stepping on each other's toes, representing orthogonal mode shapes in action.
🧠 Other Memory Gems
-
To remember the properties, think 'Mass Means No Crash' and 'Stiffness Means No Collision' for mass and stiffness orthogonality.
🎯 Super Acronyms
M.O.S. = Mass Orthogonality and Stiffness - remember the connection between the two properties.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Mode Shapes
Definition:
The specific shapes that a structure assumes during its natural vibrations.
-
Term: Orthogonality
Definition:
A property where two distinct vectors do not interfere with each other, often meaning they are independent.
-
Term: Mass Matrix [M]
Definition:
A matrix that represents the mass distribution in a mechanical or structural system.
-
Term: Stiffness Matrix [K]
Definition:
A matrix that reflects how much a structure resists deformation under applied forces.