Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Natural Frequencies and Mode Shapes
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're going to focus on how we determine natural frequencies and mode shapes for MDOF systems. Can anyone tell me why understanding these is vital for structures?
I think it helps to predict how the structure will respond to vibrations, right?
Exactly! By knowing the natural frequencies, we can predict how a building or bridge will react during an earthquake. Now, who can explain what mode shapes are?
Mode shapes represent the specific patterns of motion that occur at those natural frequencies.
Good job! Remember the acronym 'N-M-S' for Natural Frequencies and Mode Shapes to recall why they are significant: they define how structures naturally vibrate.
Seismic Response Using Modal Analysis
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let’s dive into how modal analysis helps us compute seismic responses. Who can explain what we mean by ‘modal analysis’?
I believe it's breaking down complex problems into simpler parts, right? Like analyzing each mode separately.
Exactly! This method allows us to handle the dynamic response in a more simplified way. Why do you think this could be useful?
It probably saves time and resources when analyzing large structures!
Absolutely. Let’s remember the phrase 'See M-D-A' — Simplify, Analyze, Dynamic Response. It encapsulates what we’re doing during modal analysis.
Estimation of Base Shear
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Base shear is a major concern in seismic engineering. Can someone explain what base shear means?
It's the total lateral force on the base of a structure during an earthquake, right?
Correct! And why is it important to estimate this accurately?
So we can design the foundation and structure to withstand those forces without failing.
Exactly! Use the memory aid 'B-S-A' - Base Shear Analysis for our importance slogan. It helps us remember our tasks in seismic design!
Applications of MDOF in Earthquake-Resistant Design
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let’s discuss how MDOF applications impact earthquake-resistant design. Why is this significant?
It allows engineers to design structures that can withstand all kinds of seismic forces.
Very true! And can anyone cite a real-world example where MDOF principles have been applied?
I read about how multi-story buildings incorporate MDOF to handle vibrations during earthquakes!
Excellent example! Let's summarize: MDOF systems are critical for modern structural designs to withstand seismic actions — remember 'Earthquake Profound Structural Design' or 'E-P-S-D'.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section focuses on typical problems involving MDOF systems, such as determining natural frequencies and computing seismic response. It highlights applications in earthquake-resistant design, structural health monitoring, and vibration control.
Detailed
Example Problems and Applications
In analyzing Multiple Degree of Freedom (MDOF) systems, particularly in the context of seismic activity, several key problems and applications arise. These examples demonstrate the relevance of MDOF frameworks in structural engineering and the significance of understanding their dynamic behavior. Key problems include:
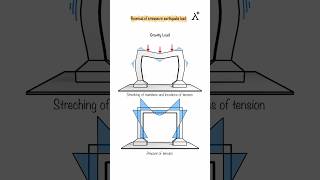
- Determining natural frequencies and mode shapes for 2-DOF and 3-DOF systems, which are crucial for predicting how structures will behave under dynamic loads.
- Computing seismic response using modal analysis, which involves breaking down complex response into manageable modal components and assessing contributions from each mode.
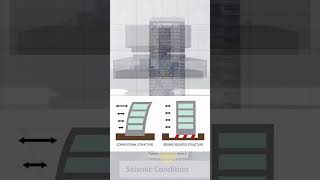
- Estimating base shear and floor accelerations, essential for ensuring that structures can withstand seismic events.
- Applying time-history and response spectrum analysis, methods that allow engineers to evaluate how structures respond to earthquake-induced ground motions and design effective protections.
Applications include:
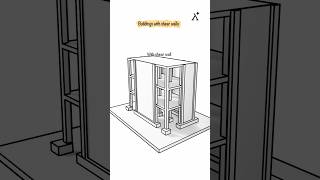
- Earthquake-resistant design, which focuses on enhancing structural integrity against seismic threats.
- Structural health monitoring, employing MDOF systems to assess and maintain the safety and performance of existing structures.
- Retrofitting and vibration control, enabling improved performance of older structures under seismic loading. These problems and applications underscore the importance of MDOF analysis in practical engineering scenarios.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Types of Example Problems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Typical problems include:
- Determining natural frequencies and mode shapes for 2-DOF and 3-DOF systems.
- Computing seismic response using modal analysis.
- Estimating base shear and floor accelerations.
Detailed Explanation
In this chunk, we discuss the types of example problems that arise when dealing with Multiple Degree of Freedom (MDOF) systems. The first type of problem involves determining the natural frequencies and mode shapes for systems with two or three degrees of freedom (DOF). Natural frequencies are the frequencies at which a system tends to oscillate in the absence of any driving force. Mode shapes are the specific patterns of motion that correspond to each natural frequency. Next, we consider how to compute the seismic response of structures using modal analysis. This method helps predict how buildings respond during seismic events by analyzing their vibrational characteristics. Lastly, we estimate base shear and floor accelerations, which are critical for understanding the forces acting on a structure during an earthquake. Base shear, in particular, refers to the total horizontal force at the base of a structure due to seismic activity.
Examples & Analogies
Think of a swing at a playground. The natural frequency of the swing is like how quickly it swings back and forth when pushed. The mode shape would be the path it traces while swinging. If the swing was a skyscraper during an earthquake, figuring out how the structure would sway (its natural frequency and mode shapes) helps engineers design it to move safely without falling over. Just as we would adjust how high we push the swing based on how heavy it is, engineers adjust designs based on the estimated forces (base shear) the building will experience during an earthquake.
Applications of MDOF Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Applications:
- Earthquake-resistant design.
- Structural health monitoring.
- Retrofitting and vibration control.
Detailed Explanation
This chunk highlights the practical applications of analyzing MDOF systems. First, earthquake-resistant design focuses on creating buildings that can withstand the forces generated during an earthquake. This involves understanding the dynamic behavior of structures and incorporating various safety features. Second, structural health monitoring involves routinely checking the structural integrity of buildings and bridges to ensure they can handle expected loads and remain safe over time. This can be done using sensors that measure vibrations and other factors. Lastly, retrofitting and vibration control entail modifying existing structures to decrease their vulnerability to seismic forces or improve performance. This might include adding dampers, reinforcements, or altering design elements to increase resilience against seismic events.
Examples & Analogies
Consider a doctor monitoring a patient's heart health. Just as the doctor uses various tools to keep track of how the heart responds under stress, engineers monitor buildings to ensure that they can handle earthquakes and other stresses. If a building shows signs of weakness, similar to how a doctor suggests treatment when a patient's heart shows problems, engineers might 'retrofit' the building, adding safety features to protect it from future disasters.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Modal Analysis: A method that simplifies responses by analyzing modes individually.
-
Base Shear: Total lateral force at the base due to seismic loading.
-
Natural Frequencies: Frequencies at which the system vibrates without external forces.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of natural frequency calculation for a 2-DOF system involving identical masses and springs.
-
Computation of base shear from modal responses for a 5-story building subjected to seismic loads.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Base shear gives a fear, when an earthquake comes near!
📖 Fascinating Stories
-
Imagine a tall building shaking during a storm. Engineers study its natural frequencies to prevent disasters — they save the day by understanding its mode shapes!
🧠 Other Memory Gems
-
Remember 'N-M-B' for Natural Frequencies, Mode Shapes, and Base Shear in your designs.
🎯 Super Acronyms
Use 'E-P-S-D' — Earthquake Profound Structural Design to remember the significance of MDOF applications.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Natural Frequencies
Definition:
The frequencies at which a system tends to oscillate in the absence of any driving force.
-
Term: Mode Shapes
Definition:
The displacement patterns of a structure at its natural frequencies.
-
Term: Base Shear
Definition:
The total lateral force at the base of a structure due to seismic activity.
-
Term: Modal Analysis
Definition:
A technique that simplifies the complex calculations in dynamic response by analyzing individual modes.