Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Control Volumes
Unlock Audio Lesson
Today, we're going to explore the concept of control volumes in fluid mechanics. Can anyone define what a control volume is?
Isn't it a fixed region in space where we analyze the flow of fluids?
Exactly! A control volume is defined as a specific region in space through which fluid flows. It's crucial for applying conservation laws. Now, what conservation laws do we typically consider?
I think it's mass, momentum, and energy conservation?
Correct! These three laws help us understand the behavior of fluids as they move in and out of these volumes. Now, can anyone give an example of a control volume in real life?
Like the flow of water through a pipe?
Exactly! Great example. A pipe can be seen as a control volume. To summarize today, control volumes allow us to apply conservation principles to analyze fluid flow effectively.
Extensive vs. Intensive Properties
Unlock Audio Lesson
Now, let's shift our focus to properties associated with fluids: extensive and intensive properties. Who can explain the difference?
Extensive properties depend on the amount of mass, while intensive properties do not?
Exactly! For instance, mass, momentum, and total energy are extensive because they grow with more mass. What about an example of an intensive property?
Velocity! It's the same regardless of how much fluid you have.
Right! Velocity and specific energy are examples of intensive properties. This distinction is key for analyzing fluid behavior. Can someone summarize why it's important to know these properties?
Understanding these properties helps us apply the right conservation equations when dealing with fluids.
Excellent summary! Remember: extensive can be imagined as 'total amount', and intensive as 'per mass unit'.
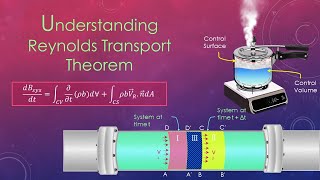
Reynolds Transport Theorem
Unlock Audio Lesson
Next, let's discuss the Reynolds Transport Theorem. Does anyone have an idea of what it represents?
It relates the conservation principles at a system level to the control volume level?
Exactly! It shows us how changes in properties within a control volume relate to influx and outflux through its boundaries. Why do you think this is useful?
It helps us analyze fluid motion by accounting for what comes in and out!
Right! Remember, for using this theorem, you'll need to differentiate between influx and outflux effectively. As we derive it, keep in mind the various components involved in that relationship. Can anyone recall how we start the derivation?
We begin by defining the control volume's limits at different time steps?
Correct! Understanding the flow over time in distinct regions is critical for this theorem. Summing all up, the Reynolds Transport Theorem validates conservation laws within a defined space.
Practical Applications of Control Volumes
Unlock Audio Lesson
Now that we've understood the theory, let's anticipate some practical applications of control volumes. Why do we utilize these principles in engineering?
To optimize systems like pumps, piping, and any fluid machinery!
Absolutely right! By analyzing control volumes, engineers can predict how systems behave under various conditions. Can anyone give an instance in which this knowledge might be crucial?
Designing water treatment facilities would require this to ensure proper flow rates.
Exactly! Understanding the influx and outflux is fundamental to ensuring efficiency and safety. Wrapping up, applying control volume analysis is vital in many engineering aspects—always connect theory to practice!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we delve into how momentum and energy conservation principles apply to control volumes in fluid mechanics. The section also introduces the Reynolds Transport Theorem, differentiates between extensive and intensive properties, and provides foundational knowledge for analyzing fluid systems through control volumes.
Detailed
Control Volume and Influx/Outflux Regions
In fluid mechanics, the behavior of fluids in various control volumes is governed by the principles of conservation laws—mass, momentum, and energy. The section begins by discussing how these conservation laws relate to fluid motion and the forces acting on fluids. It emphasizes the significance of understanding how fluids transfer energy and momentum and describes the corresponding forces through specific velocity fields.
Key Conservation Principles
- Conservation of Mass: The mass within a control volume remains constant unless acted upon by an external flux.
- Conservation of Momentum: The momentum of fluid within a control volume changes due to the forces exerted by the fluid itself and any external interactions.
- Conservation of Energy: The energy, including work done and heat transfer, is transformed as fluid particles move from one location to another.
Extensive vs. Intensive Properties
- Extensive Properties: These properties, such as mass, momentum, and energy, are proportional to the amount of substance in the control volume. As mass increases, extensive properties increase correspondingly.
- Intensive Properties: These properties, including velocity and specific energy, are independent of the mass and represent characteristics of the system per unit mass.
Importance of the Reynolds Transport Theorem
The Reynolds Transport Theorem elegantly links the conservation laws at the system level with those applicable to control volumes, allowing for a comprehensive analysis of fluid dynamics. The derivation showcases the relationship between the extensive properties and their time rates of change in a control volume versus a system approach. The theorem also facilitates understanding of influx and outflux regions, totaling conservation quantities as they enter and exit the control volume.
In summary, this section forms the backbone for advancing into fluid dynamics analyses, providing the foundational tools necessary to solve complex motion and energy problems in fluids.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Conservation Principles
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The conservation of momentum which is required for you to know it, how the fluid particles are moving it, what could be the force exerting on that, what could be the velocity. Similar way, we can understand the energy conservation which plays a major role for us when the fluid comes from one location to other locations, how much of work is done by the fluid or into the fluid.
Detailed Explanation
In understanding fluid mechanics, we need to look at the conservation of momentum and energy. Conservation of momentum refers to how the motion of fluid particles is influenced by the forces acting on them, including their velocity. On the other hand, energy conservation helps us understand how much work fluid can do as it moves from one place to another. This involves tracking changes in energy as fluid flows, such as when it is compressed or expanded.
Examples & Analogies
Think about riding a bicycle. As you pedal (apply a force), you accelerate (momentum conservation) due to your effort. If you're going downhill, the gravitational energy (energy conservation) can help you go faster without having to pedal as hard because the energy is transforming in the system.
Energy Transfer and Heat Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Similar way, whether there is heat transfers happening which you can feel it, if there is a temperature gradient there will be heat transfer either to the surrendering of the systems or into the systems or out of the system, that is what we can do.
Detailed Explanation
Heat transfer is another vital aspect to consider. When there is a difference in temperature (a temperature gradient), heat will always flow from the hotter area to the cooler area until equilibrium is reached. This can mean heat moving into the system, out of the system, or being exchanged between systems.
Examples & Analogies
Imagine a cup of hot coffee in a cold room. The heat from the coffee moves into the air around it, causing the coffee to cool down and the air to warm up. Eventually, the temperature of the coffee and the surrounding air approaches equilibrium.
Extensive vs. Intensive Properties
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, let me define two types of properties that we have; one is called extensive property and the other is the intensive property. The extensive property which is considered as proportional to the amount of mass. When you apply extensive properties, that means you are the properties which are proportional to the amount of mass.
Detailed Explanation
Extensive properties are characteristics that depend on the amount of substance present. Examples include mass, volume, and total energy. For instance, doubling the amount of water will double its mass and volume. Intensive properties, however, are independent of the amount of substance. These include temperature and density, which remain constant regardless of how much of the substance is present.
Examples & Analogies
Think of making soup. If you double the ingredients (extensive property), you double the volume of the soup. However, the temperature of the soup, whether it's hot or cold, does not depend on the total amount but rather the heat applied to it.
Reynolds Transport Theorem Overview
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, we will go to derive Reynolds transport theorem. The derivation of the Reynolds transport theorem are available in almost all the fluid mechanics books.
Detailed Explanation
The Reynolds transport theorem links the rate of change of a property within a control volume to the flux of that property across the control surface. It's fundamental for analyzing fluid motion in control volumes, providing a clear method to account for how properties like mass, momentum, and energy are conserved.
Examples & Analogies
Imagine a water tank with a hose filling it at one end and a drain at the other. The Reynolds transport theorem helps you understand how the water level changes inside the tank by considering how much water flows in through the hose (influx) and how much drains out (outflux).
Control Volume Definition
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us understand the Reynolds transport theorem which establish the relationship between the conservation law at the system level and the conservation at the control volume level.
Detailed Explanation
A control volume is a fixed or moving region in space through which fluid flows. This concept allows us to analyze physical phenomena and derive important equations for mass, momentum, and energy conservation. It establishes a boundary around a system to facilitate easier calculations and understanding of fluid motion.
Examples & Analogies
Think of a car moving through air. The car itself can be seen as a control volume because it interacts with the air around it. By understanding how air flows into and out of this control volume (the car's boundaries), we can solve problems related to aerodynamics.
Influx and Outflux Regions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let me define this 3 into 3 different spaces, like the space defined by this part I can give it as I and this can be II and this can be used as the control volume space.
Detailed Explanation
The control volume is often divided into regions based on fluid movement. These can be defined as influx (where fluid enters), outflux (where fluid exits), and a common region (where fluid exists at both times t and t+dt). This classification helps in understanding how properties change within the control volume over time.
Examples & Analogies
Imagine pouring water into a glass. The area where water enters the glass is the influx region, while the area where it might overflow is the outflux region. Understanding these regions helps you predict how full the glass will get over time.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Control Volume: A defined region in space used for analysis of fluid flow.
-
Conservation Laws: Principles governing the behavior of mass, momentum, and energy.
-
Extensive Property: Properties depending on the amount of mass in a system.
-
Intensive Property: Properties independent of the mass of a substance.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A pipe serving as a control volume for analyzing the flow of water.
-
Using conservation of energy to understand how a dam generates electricity utilizing falling water.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Control, control, fluid flow, mass and energy always grow.
📖 Fascinating Stories
-
Imagine a town collecting rainwater in various buckets, each bucket representing a control volume contributing flux when filled (influx), and draining when full (outflux).
🧠 Other Memory Gems
-
To remember extensive and intensive properties: E for Extensive is for Everything (mass), I for Intensive is Independent (temperature).
🎯 Super Acronyms
MEM
- Mass
- Energy
- Momentum - the three conservation principles to remember!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Conservation of Mass
Definition:
A principle stating that the mass of a closed system remains constant over time.
-
Term: Conservation of Momentum
Definition:
A principle asserting that the total momentum of a closed system remains constant unless acted upon by external forces.
-
Term: Conservation of Energy
Definition:
The principle that energy cannot be created or destroyed, only transformed from one form to another.
-
Term: Extensive Property
Definition:
Properties that depend on the mass of the substance present, such as mass, momentum, and energy.
-
Term: Intensive Property
Definition:
Properties that do not depend on the quantity of substance, such as temperature, pressure, and specific energy.
-
Term: Reynolds Transport Theorem
Definition:
A fundamental theorem in fluid dynamics relating system-level changes of property to control volume dynamics.
-
Term: Influx
Definition:
The quantity of fluid entering a control volume.
-
Term: Outflux
Definition:
The quantity of fluid exiting a control volume.